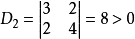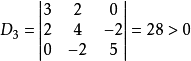通俗理解
首先半正定矩阵定义为:
其中$X$是向量,$M$是变换矩阵
我们换一个思路看这个问题,矩阵变换中,$MX$代表对向量$X$进行变换,我们假设变换后的向量为$Y$,记做$Y=MX$。于是半正定矩阵可以写成:
这个是不是很熟悉呢? 他是两个向量的内积。 同时我们也有公式:
$||X||,||Y||$代表向量$X,Y$的长度,$\theta$是他们之间的夹角。 于是半正定矩阵意味着$cos(\theta) \geq 0$, 这下明白了么?
正定、半正定矩阵的直觉代表一个向量经过它的变化后的向量与其本身的夹角小于等于90度。
证明
矩阵$A$正定是指,对任意的$X≠0$恒有$X^TAX>0$。
矩阵$A$半正定是指,对任意的$X≠0$恒有$X^TAX≥0$。
判定$A$是半正定矩阵的充要条件是:A的所有顺序主子式大于或等于零。
顺序主子式
设$A$为$n \times n$阶矩阵,子式

称为$A$的$i$阶顺序主子式
例如,$3 \times 3$矩阵

则$A$的顺序主子式为: