向量的内积
也称为向量的的数量积、点积
代数定义
n维平面上有,向量$a$为$[a_1,a_2,…,a_n]$,向量$b$为$[b_1,b_2,…,b_n]$。则向量$a$和向量$b$的点积公式为:
注意:上面得到的最终为标量。
几何定义
设二维空间中有两个向量$a$和$b$,$\mid a \mid$和$\mid b \mid$分别为向量$a$和$b$的大小,它们的夹角为$\theta(0\leq \theta \leq \pi)$,则内积定义为以下实数:
接着将上述定义扩展到$n$维,向量$a$和向量$b$的夹角定义为:
所以就有
向量内积的几何和物理意义
向量内积的几何解释就是一个向量在另一个向量上的投影的积,也就是同方向的积
特别的,如果一个向量如$a$是某个坐标轴的单位坐标向量,那么,两个向量的内积$a \cdot b$就是向量$b$在此坐标轴上的坐标值。这个结论非常重要,这是傅立叶分析的理论基础。
其他几何意义:从内积数值上我们可以看出两个向量的在方向上的接近程度。当内积值为正值时,两个向量大致指向相同的方向(方向夹角小于90度);当内积值为负值时,两个向量大致指向相反的方向(方向角大于90度);当内积值为0时,两个向量互相垂直。
向量内积的生活解释:单价向量乘以数量向量,得到总价格
向量内积的物理解释:一个斜坡上用力$F$斜上拉一个物体,位移为$S$(没有重力的情况下),那么这个力$F$所作的功:$w=FScos\theta$
向量的外积
也称为向量的向量积、叉积
定义:两个向量$a$和$b$的向量积(外积、叉积)是一个向量,记作$a×b$.
- 若$a、b$不共线,则$a×b$的模是:$∣a×b∣=|a|·|b|·sin〈a,b〉$;$a×b$的方向是:垂直于$a$和$b$,且$a、b$和$a×b$按这个次序构成右手系.
- 若$a、b$共线,则$a×b=0$,注意这里的$0$为零向量。
向量外积的几何意义:
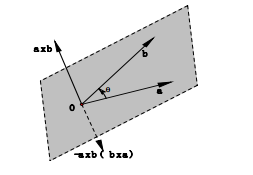
$a × b$为一个新生成的向量,这个向量垂直于$a$ 和$ b$展成的平面(图中的虚线平行四边形,由线段$oa$和$ob$所确定的平面);同样向量$b × a$也垂直这个平面,但方向与$a × b$所指的方向相反,即$a × b = - b × a$(右手法则)
向量外积的物理意义:
物理上称为轴向量
1、知道陀螺的原理吗?高速旋转的陀螺会定向。陀螺所定义的方向就是矢径向量$r$和线速度$v$叉乘结果角速度$ω$方向。
2、螺钉,螺钉只要左右向旋转即可在螺孔中前进或者后退。用螺丝刀把这棵螺钉按照$F+$的方向右旋,那么旋转时的扭力向量$F$和矢径向量$r$这两个叉乘的结果即是力矩$M$的方向,这棵螺钉就会沿着力矩$M$在螺母孔内前进,反方向就会改变叉积的方向进而退出螺孔(右螺旋螺钉)。也就是力矩或叉乘向量的方向就是螺钉的螺旋前进的方向,这个方向垂直于螺丝刀口和扭力的方向,也就是垂直于被叉积的两个向量的方向。
3、我们经常骑的自行车,车子静止的时候我们在车上会摔下来,一旦骑行起来,车子就会平稳而不会左右倾倒,这也是叉积的功劳(与陀螺的原理相同)。
向量混合运算的几何意义
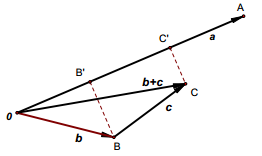
向量加法的结合律的几何解释
向量混合运算的几何意义
向量加法的结合律的几何解释

向量数乘的分配律的几何解释

向量点积的分配律的几何解释
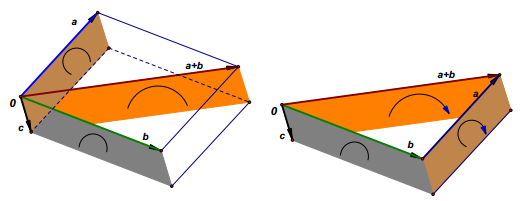
向量叉积的分配律的几何解释
如下图:面向量,有向面积满足平行四边形法则、三角形法则
向量的混合积的几何解释
三向量的混合积有关系$(a\times b)\cdot c=(b\times c)\cdot a=(c\times a)\cdot b$,且其中$(a\times b)\cdot c=\mid a\times b \mid \mid c \mid cos\alpha$

以向量$a,b,c$为棱的平行六面体的底(平行四边形$0ADB$)的面积$S$在数值上等于$|a×b|$,它的高$h$等于向量$c$在向量$a×b$上的投影,即$h =|c| cos a$ ,所以平行六面体的体积等于
向量的投影和几何解释
多个向量在任意轴上的投影和
多个或有限个向量的和在任意轴上投影等于各个向量在同一轴上投影的和。
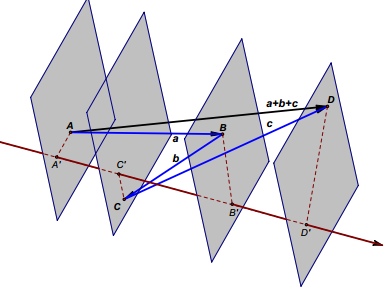
图示是显然的,$A’B’+B’C’+C’D’=A’D’$,命题得解。
多个向量在任意平面上的投影和
多个或有限个向量的和在任意平面上投影等于各个向量在同一平面上投影的和。

变向量的几何意义:
对于用数组$(a_1,a_2,…a_n)$表示的向量a,如果数组中的元素部分或者全部是变量,那么这个变向量在$n$维坐标系下表示的几何图形是什么呢?
二维变向量的几何图形
- 变向量$(x_1,x_2)$的几何图形表示为一个平面
- 变向量$(x_2,a_2)$表示的是直线$x_2=a_2$
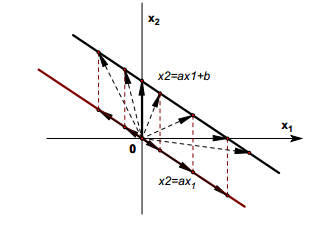
- 变向量$(x_1,ax_1+b)$表示的是直线$x_2=ax_1+b$
- 变向量$(x_1,ax_1)$就表示为一条过原点的直线$(x_1,ax_1+b)=$(x_1,ax_1)$+(0,b)$

三维变量的几何图形:
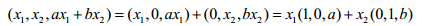
这个平面是一个向量空间,一个被常向量 和
和 所张成的向量平面空间,记为
所张成的向量平面空间,记为 。因此,我们可以有这样的一个等价式:
。因此,我们可以有这样的一个等价式:
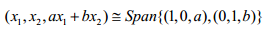

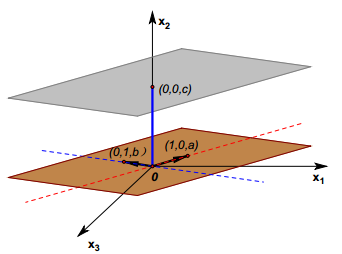
得到的新图形仍然是个平面,只是沿着向量(0,0,c) 的方向平移了长度为c的距离。
一个变向量是和一个解析方程或方程组相对应的,因此变向量和方程一样能表示一个几何图形。实际上,变向量也叫向量函数。

