函数求导

四则运算的求导法则

定理1：函数$u = u(x)$ 及 $v = v(x)$都在$x$具有导数$\Longrightarrow u(x)$ 及 $v(x)$的和、差、积、商(除分母为0的点外)都在点$x$可导，则

$$[u(x) \pm v(x)]^{\prime} = u^{\prime}(x) \pm v^{\prime}(x) \\ [u(x)v(x)]^{\prime} = u^{\prime}(x) v(x) + u(x)v^{\prime}(x) \\ [\dfrac{u(x)}{v(x)}]^{\prime} = \dfrac{u^{\prime}(x)v(x) - u(x)v^{\prime}(x)}{v^2{x}} \quad (v(x) \neq 0)$$

用导数的定义可以证明上面的3个公式

推论：

$$(Cu)^{\prime} = Cu^{\prime} (C为常数) \\ (uvw)^{\prime} = u^{\prime}vw + uv^{\prime}w + uvw^{\prime} \\ (log_a{x})^{\prime} = \big( \dfrac{\ln {x}}{\ln {a}} \big)^{\prime} = \dfrac{1}{x \ln{a}} \\ (\dfrac{C}{v})^{\prime} = \dfrac{-Cv^{\prime}}{v^2}(C为常数) \\ (u + v -w)^{\prime} = u^{\prime} + v^{\prime} - w^{\prime}$$

例1. $y = \sqrt{x}(x^3 - 4\cos{x} - sin{1}), 求y^{\prime}及\left. y^{\prime} \right|_{x = 1} $

$$\color{blue}{解： y^{\prime} = \dfrac{1}{2}\dfrac{x^3 - 4\cos{x} - sin{1}}{\sqrt{x}} + \sqrt{x} (3x^2 + 4\sin{x} - 0) = \dfrac{7x^3 +8x \sin{x} -4\cos{x} - \sin1}{2\sqrt{x}} \left. y^{\prime} \right|_{x = 1} \\ = \dfrac{7 + 7\sin{1} - 4\cos{1}}{2} \\ = \dfrac{7}{2} + \dfrac{7}{2}{sin{1}} - 2\cos{1} }$$

例2.求证$(\tan{x})^{\prime} = \sec^2{x}, (\csc{x})^{\prime} = -\csc{x} \cot{x} $

证：

$$\color{blue}{ (\tan{x})^{\prime} = \Big( \dfrac{\sin{x}}{\cos{x}} \Big)^{\prime} \\ = \dfrac{\sin^{\prime}{x} \cos{x} - \sin{x} \cos^{\prime}{x}}{\cos^2{x}} \\ = \dfrac{\cos^2{x} + \sin^2{x}}{\cos^2{x}} \\ = \dfrac{1}{\cos^2{x}} \\ = \sec^2{x} \\ \ \\\ (\csc{x})^{\prime} = \Big( \dfrac{1}{\sin{x}} \Big)^{\prime} \\ = \dfrac{-(\sin{x})^{\prime}}{\sin^2{x}} \\ = -\dfrac{\cos{x}}{\sin{x} \sin{x}} \\ = -\csc{x} \cot{x} \\ \ \\ 类似可证：\\ (\cot{x})^{\prime} = -\csc^2{x}, \\ (sec{x})^{\prime} = \sec{x} \tan{x} }$$

复合函数的求导法则

定理2：$u=g(x)$在点$x$可导, $y = f(u)$在点$u=g(x)$可导$\Longrightarrow$复合函数$y= f[g(x)]$在点$x$可导，且$\dfrac{dy}{dx} = f^{\prime}(u)g^{\prime}(x)$.

证：

$$\color{blue}{ \because y = f(u)在点u可导，故\lim_{\Delta{u} \rightarrow 0}{\dfrac{\Delta{y}}{\Delta{x}}} = f^{\prime}(u) \\ 即 \dfrac{\Delta{y}}{\Delta{u}} = f^{\prime}(u) + \alpha \\ \therefore \Delta{y} = f^{\prime}{\Delta{u}} + \alpha {\Delta{u}} (当\Delta{u} \rightarrow 0时\alpha \rightarrow 0) \\ 故有 \quad \dfrac{\Delta{y}}{\Delta{x}} = f^{\prime}(u) \dfrac{\Delta{u}}{\Delta{x}} + \alpha \dfrac{\Delta{u}}{\Delta{x}} (\Delta{x} \neq 0) \\ \therefore \dfrac{dy}{dx} = \lim_{\Delta{x} \rightarrow 0}{\dfrac{\Delta{y}}{\Delta{x}}} = \lim_{\Delta{x} \rightarrow 0}{[f^{\prime}(u)\dfrac{\Delta{u}}{\Delta{x}} + \alpha \dfrac{\Delta{u}}{\Delta{x}} ] } \\ = f^{\prime}(u)g^{\prime}(x) }$$

推广：此法则可推广到多个中间变量的情形

例如：$y = f(u), u = \varphi(v), v = \psi(x) $
$\dfrac{dy}{dx} = \dfrac{dy}{du} \cdot \dfrac{du}{dv} \cdot \dfrac{dv}{dx} $
$= f^{\prime}(u) \cdot \varphi^{\prime}(v) \cdot \psi^{\prime}(x)$

例3.求下列导数：$(1)(x^{\mu})^{\prime};(2) (x^x)^{\prime}; (3)(\sinh {x})^{\prime} $

解：

$$\color{blue}{ (1)(x^{\mu})^{\prime} = (e^{\mu \ln{x}})^{\prime} = e^{\mu \ln{x}} \cdot (\mu \ln{x}){\prime} = x^{\mu} \cdot \dfrac{\mu}{x} = \mu x^{\mu - 1} \\ (2) (x^x)^{\prime} = (e^{x \ln{x}})^{\prime} = (e^{x \ln{x}})^{\prime} \cdot (x \ln{x})^{\prime} \\ = x^x(\ln{x} + 1) \\ (3) (\sinh {x})^{\prime} = (\dfrac{e^{x} - e^{-x}}{2})^{\prime} = \dfrac{e^{x} + e^{-x}}{2} = \cosh{x} \\ 说明：类似可得 \\ (cosh{x})^{\prime} = \sinh{x}; (tanh{x})^{\prime} = \dfrac{1}{cosh^2{x}};(a^x)^{\prime} = e^{x \ln{a}}}$$

例4.设 $y = \ln{\cos(e^x)}$,求$\dfrac{dy}{dx}$

解：

$$\color{blue}{ \dfrac{dy}{dx} = \dfrac{1}{cos(e^x)} \cdot (-sin(e^x)) \cdot e^x \\ = -e^x \tan(e^x) }$$

多元复合函数的求导法则

设有一元复合函数：$ y = f(u), u = \varphi(x)$，则有下面的法则
求导法则：$\quad \dfrac{dy}{dx} = \dfrac{dy}{du} \cdot \dfrac{du}{dx}$
微分法则：$\quad dy = f^{\prime}(u)du = f^{\prime}(u)\varphi^{\prime}(x)dx$

定理：若函数$u = \varphi(t),v = \psi(t)$在点$t$可导,$ z=f(u, v)$在点$(u, v)$处偏导连续,则复合函数$z = f(\varphi(t), \psi(t))$在点$t$可导,且有链式法则

$$\dfrac{dz}{dt} = \dfrac{\partial z}{\partial u} \cdot \dfrac{du}{dt} + \dfrac{\partial z}{\partial v} \cdot \dfrac{dv}{dt}$$

证:

$$设t取增量\Delta{t},则相应中间变量有增量\Delta{u}, \Delta{v}, \\ \Delta{z} = \dfrac{\partial z}{\partial u} \Delta{u} + \dfrac{\partial z}{\partial v} \Delta{v} + o(\rho) \quad (\rho = \sqrt{(\Delta{u})^2 + (\Delta{v})^2}) \\ 两边同时除以\Delta{t}\\ \dfrac{\Delta{z}}{\Delta{t}} = \dfrac{\partial z}{\partial u} \cdot \dfrac{du}{dt} + \dfrac{\partial z}{\partial v} \cdot \dfrac{dv}{dt} + \dfrac{o(\rho)}{\Delta{t}} \quad (\rho = \sqrt{(\Delta{u})^2 + (\Delta{v})^2}) \\ 令\Delta{t} \rightarrow 0, 则有\Delta{u} \rightarrow 0, \Delta{u} \rightarrow 0 \\ \dfrac{\Delta{u}}{\Delta{t}} \rightarrow \dfrac{du}{dt}, \dfrac{\Delta{v}}{\Delta{t}} \rightarrow \dfrac{dv}{dt} \\ \dfrac{o(\rho)}{\Delta{t}} = \dfrac{o(\rho)}{\rho} \sqrt{(\dfrac{\Delta{u}}{\Delta{t}})^2 + (\dfrac{\Delta{v}}{\Delta{t}})^2} \rightarrow 0 (\Delta{t} < 0时，根式前加”-“号) \\ \sqrt{(\dfrac{\Delta{u}}{\Delta{t}})^2 + (\dfrac{\Delta{v}}{\Delta{t}})^2}是常数，\dfrac{o(\rho)}{\rho} \rightarrow 0 \\ \therefore \dfrac{dz}{dt} = \dfrac{\partial z}{\partial u} \cdot \dfrac{du}{dt} + \dfrac{\partial z}{\partial v} \cdot \dfrac{dv}{dt} (全导数公式)$$

推广: 中间变量是多元函数的情形.例如
$z = f(u, v), u = \varphi(x, y), v = \psi(x, y)$

$$\dfrac{\partial z}{\partial x} = \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial x} + \dfrac{\partial z}{\partial v} \cdot \dfrac{\partial v}{\partial x} = f_1^{\prime}\varphi_1^{\prime} + f_2^{\prime}\psi_1^{\prime} \\ \dfrac{\partial z}{\partial y} = \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial y} + \dfrac{\partial z}{\partial v} \cdot \dfrac{\partial v}{\partial y} = f_1^{\prime}\varphi_2^{\prime} + f_2^{\prime}\psi_2^{\prime}$$

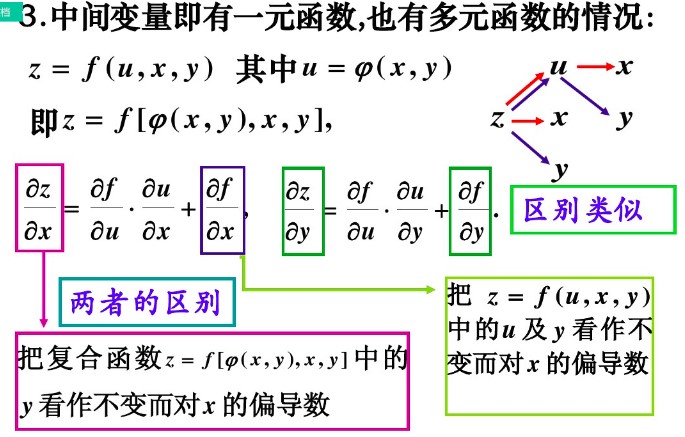
又如，$z = f(x, v), v = \psi(x, y) $，当他们都具有可微条件时,有

$$\dfrac{\partial z}{\partial x} = \dfrac{\partial f}{\partial x} + \dfrac{\partial f}{\partial v} \cdot \dfrac{\partial v}{\partial x} = f_1^{\prime} + f_2^{\prime}\psi_1^{\prime} \\ \dfrac{\partial z}{\partial y} = \dfrac{\partial f}{\partial v} \cdot \dfrac{\partial v}{\partial y} = f_2^{\prime}\psi_2^{\prime}$$

注意：$这里\dfrac{\partial z}{\partial x} 与\dfrac{\partial f}{\partial x}不同, \dfrac{\partial z}{\partial x}表示固定y对x求导, \dfrac{\partial f}{\partial x}表示固定v对x求导$

口诀：分段用乘，分叉用加，单路全导，叉路偏导

例1.$设z = e^u \sin{v}, u = xy, v = x + y,求\dfrac{\partial z}{\partial x}, \dfrac{\partial z}{\partial y}$

解:

$$\dfrac{\partial z}{\partial x} = \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial x} + \dfrac{\partial z}{\partial v} \cdot \dfrac{\partial v}{\partial x} \\ = e^u\sin{v} \cdot y + e^u \cos{v} \cdot 1 \\ = e^u(y\sin{v} + \cos{v}) \\ = e^{xy}[y\sin{(x + y)} + \cos{(x + y)}] \\ \dfrac{\partial z}{\partial y} = \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial y} + \dfrac{\partial z}{\partial v} \cdot \dfrac{\partial v}{\partial y} \\ = e^u\sin{v} \cdot x + e^u \cos{v} \cdot 1 \\ = e^u(x\sin{v} + \cos{v}) \\ = e^{xy}[x\sin{(x + y)} + \cos{(x + y)}]$$

例2.$设z = uv + \sin{t}, u = e^t, v = cos{t},求全导数\dfrac{dz}{dt}$

解:

$$\dfrac{dz}{dt} = \dfrac{\partial z}{\partial u} \cdot \dfrac{du}{dt} + \dfrac{\partial z}{\partial v} \cdot \dfrac{dv}{dt} + \dfrac{\partial z}{\partial t} \\ = v \cdot e^t + u \cdot (-\sin{t}) + \cos{t}\\ = e^t(\cos{t} - \sin{t}) + \cos{t}$$

注意：多元抽象复合函数求偏微分方程变形与验证解的问题中经常遇到,下列两个例题有助于掌握这方面问题和常用的导数符号注意：多元抽象复合函数求偏微分方程变形与验证解的问题中经常遇到,下列两个例题有助于掌握这方面问题和常用的导数符号

1) 已知$f(x, y)| _ {y = x^2} = 1, f_1^{\prime}(x, y) | _ {y = x^2} = 2x,求f_2^{\prime}(x, y) | _ {y = x^2}$

解:

$$由f(x, x^2) = 1两边对x求导,得\\ f_1^{\prime}(x, x^2) + f_2^{\prime}(x, x^2)\cdot 2x = 0\\ 2x[1 + f_2^{\prime}(x, x^2)] = 0 \\ f_2^{\prime}(x, x^2) = -1 \\ 即f_2^{\prime}(x, y) | _ {y = x^2} = -1$$

2) $设z = \sin(xy^2),求\dfrac{\partial z}{\partial x}, \dfrac{\partial z}{\partial y}$

解:

$$令u = xy^2, 则z = \sin{u} \\ \dfrac{\partial z}{\partial x} = \dfrac{dz}{du} \cdot \dfrac{\partial u}{\partial x} = \cos{u} \cdot y^2 = y^2 \cos(xy^2) \\ \dfrac{\partial z}{\partial y} = \dfrac{dz}{du} \cdot \dfrac{\partial u}{\partial y} = \cos{u} \cdot 2xy = 2xy \cos{(xy^2)}$$

3) $设z = f(x^2y, y^2),求\dfrac{\partial z}{\partial x}, \dfrac{\partial z}{\partial y}$

解:

$$令u = x^2y, v = y^2 \\ \dfrac{\partial z}{\partial x} = \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial x} + \dfrac{\partial z}{\partial v} \cdot \dfrac{\partial v}{\partial x} \\ = f_1^{\prime}(u, v) \cdot 2xy + f_2^{\prime}(u, v) \cdot 0 \\ = 2xy \cdot f_1^{\prime}(x^2y, y^2) \\ \dfrac{\partial z}{\partial y} = \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial y} + \dfrac{\partial z}{\partial v} \cdot \dfrac{\partial v}{\partial y} \\ = f_2^{\prime}(u, v) \cdot x^2 + f_2^{\prime}(u, v) \cdot 2y \\ = f_2^{\prime}(x^2y, y^2) \cdot x^2+ f_2^{\prime}(x^2y, y^2) \cdot 2y$$

4) $设z = f(\dfrac{y}{x}), f(u)为可微函数，证明: x\dfrac{\partial z}{\partial x} + y\dfrac{\partial z}{\partial y} = 0$

证:

$$u = \dfrac{y}{x} \\ x\dfrac{\partial z}{\partial x} + y\dfrac{\partial z}{\partial y} \\ = x \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial x} + y \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial y} \\ = x \dfrac{\partial z}{\partial u} \cdot \dfrac{-y}{x^2} + y \dfrac{\partial z}{\partial u} \cdot \dfrac{1}{x} \\ = \dfrac{\partial z}{\partial u} \cdot \dfrac{y - y}{x} \\ = 0$$

5) $设z = (x + 2y)^{(x + 2y)}, 求\dfrac{\partial z}{\partial x}, \dfrac{\partial z}{\partial y}$

解:

$$令u = x + 2y, v = x + 2y, z = u^v\\ \dfrac{\partial z}{\partial x} = \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial x} + \dfrac{\partial z}{\partial v} \cdot \dfrac{\partial v}{\partial x} \\ = vu^{v - 1} \cdot 1 + u^v \ln{u} \cdot 1 \\ = (x +2y)(x + 2y)^{(x + 2y - 1)} + (x + 2y)^{(x + 2y)} \ln{(x + 2y)} \\ = (x + 2y)^{(x + 2y)} (1 + ln{(x + 2y)}) \\ \dfrac{\partial z}{\partial y} = \dfrac{\partial z}{\partial u} \cdot \dfrac{\partial u}{\partial y} + \dfrac{\partial z}{\partial v} \cdot \dfrac{\partial v}{\partial y} \\ = vu^{v - 1} \cdot 2 + u^v \ln{u} \cdot 2 \\ = 2(x +2y)(x + 2y)^{(x + 2y - 1)} + 2(x + 2y)^{(x + 2y)} \ln{(x + 2y)} \\ = 2(x + 2y)^{(x + 2y)} (1 + ln{(x + 2y)})$$

初等函数的求导问题

常数和基本初等函数的导数(P94)

$$\color{blue}{ (C)^{\prime} = 0 \quad (x^{\mu})^{\prime} = \mu x^{\mu - 1} \\ (\sin{x})^{\prime} = \cos{x} \quad (\cos{x})^{\prime} = -\sin{x} \\ (\tan{x})^{\prime} = \sec^2{x} \quad (\cot{x})^{\prime} = -\csc^2{x} \\ (\sec{x})^{\prime} = \sec{x}\tan{x} \quad (\csc{x})^{\prime} = -csc{x} \cot{x} \\ (a^x)^{\prime} = a^x \ln{a} \quad (e^x)^{\prime} = e^x \\ (\log_a{x})^{\prime} = \dfrac{1}{x \ln{a}} \quad (\ln{x})^{\prime} = \dfrac{1}{x} \\ }$$

有限次四则运算的求导法则

$$\color{blue}{(u \pm v)^{\prime} = u^{\prime} \pm v^{\prime} \quad (Cu)^{\prime} = Cu^{\prime} \\ (uv)^{\prime} = u^{\prime}v + uv^{\prime} \quad (\dfrac{u}{v})^{\prime} = \dfrac{u^{\prime}v - uv^{\prime}}{v^2} \quad (v \neq 0) }$$

复合函数的求导法则

$\color{blue}{
y = f(u), u = \varphi(x) \\
\dfrac{dy}{dx} = \dfrac{dy}{du} \cdot \dfrac{du}{dx} = f^{\prime}(u) \cdot \varphi^{\prime}(x)
}$

初等函数在定义域区间内可导，且导数仍为初等函数

说明：最基本的公式：

$$(C)^{\prime} = 0 \\ (\sin{x})^{\prime} = \cos{x} \\ (\ln{x})^{\prime} = \dfrac{1}{x}$$

内容小结

求导公式及求导法则(P94)

注意:

$1)(uv)^{\prime} \neq u^{\prime}v^{\prime}, \quad (\dfrac{u}{v})^{\prime} \neq \dfrac{u^{\prime}}{v^{\prime}}$

2)搞清楚复合函数结构，有外向内逐层求导.

参考

高数 02.02函数的求导法则
高数 07.04 多元复合函数的求导法则