深度神经网络（Deep Neural Networks，以下简称DNN）是深度学习的基础，而要理解DNN，首先我们要理解DNN模型，下面我们就对DNN的模型、前向传播算法与反向传播算法做一个总结。

从感知机到神经网络

在感知机原理小结中，作者介绍过感知机的模型，它是一个有若干输入和一个输出的模型，如下图:

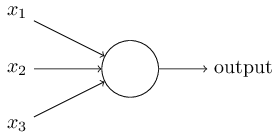
输出和输入之间学习到一个线性关系，得到中间输出结果：

感知机可以说是最古老的分类方法之一了，在1957年就已经提出。今天看来它的分类模型在大多数时候泛化能力不强，但是它的原理却值得好好研究。因为研究透了感知机模型，学习支持向量机的话会降低不少难度。同时如果研究透了感知机模型，再学习神经网络，深度学习，也是一个很好的起点。这里对感知机的原理做一个小结。

感知机模型

感知机的思想很简单，比如我们在一个平台上有很多的男孩女孩，感知机的模型就是尝试找到一条直线，能够把所有的男孩和女孩隔离开。放到三维空间或者更高维的空间，感知机的模型就是尝试找到一个超平面，能够把所有的二元类别隔离开。当然你会问，如果我们找不到这么一条直线的话怎么办？找不到的话那就意味着类别线性不可分，也就意味着感知机模型不适合你的数据的分类。使用感知机一个最大的前提，就是数据是线性可分的。这严重限制了感知机的使用场景。它的分类竞争对手在面对不可分的情况时，比如支持向量机可以通过核技巧来让数据在高维可分，神经网络可以通过激活函数和增加隐藏层来让数据可分。

用数学的语言来说，如果我们有m个样本，每个样本对应于n维特征和一个二元类别输出，如下：

我们的目标是找到这样一个超平面，即：

问题：VS2015community 无法查找或打开 pdb 文件

解决办法：

1.点击工具->选项， 在选项窗口中展开左侧菜单；

2.展开调试->常规，然后在右边的窗格中勾选“启用服务器支持”；

3.然后展开调试->符号，勾选“Windows符号服务器”，弹出的警告对话框，点击“确定”关闭选项窗口；

准备

• 英伟达显卡驱动安装包:391.35-desktop-win10-64bit-international-whql.exe
• CUDA8.0:cuda_8.0.61_win10.exe，下载地址
• CUDNN6.0:cudnn-8.0-windows10-x64-v6.0.zip，下载地址

安装英伟达显卡驱动

这个步骤没啥好说的，一步步默认方式安装，进行下去就行了。

安装CUDA8.0

解决方案和项目文件夹包含关系(c++项目)

VS解决方案和各个项目文件夹以及解决方案和各个项目对应的配置文件包含关系，假设新建一个项目ssyy，解决方案起名fangan，注意解决方案包括项目，此时生成的最外层目录为fangan代表整个解决方案的内容都在这个文件夹内。在这个fangan文件夹内包含有fangan.sln的解决方案配置文件和一个ssyy文件夹，ssyy文件夹代表整个ssyy项目的所有内容都在这个文件夹内，这个文件夹内含有ssyy.vcproj的项目配置文件和.h头文件以及.cpp源文件。如果在fangan解决方案下再建立一个新项目名为ssyy2，则会在fangan文件夹下生成一个ssyy2文件夹存放ssyy2项目的所有内容。

由上面叙述可以总结出，管理器（解决方案或项目）都会对应一个总的文件夹，这个管理器文件夹下存放本管理器的配置文件以及子管理器。比如，解决方案是个管理器，它的文件夹下含有.sln配置文件以及子管理器ssyy项目和子管理器ssyy2项目。

另外，默认情况下，项目属性设置的目录起点为项目配置文件所在位置，实际上就是项目头文件和源文件所在位置。

补充：vs中建立默认的C#项目和建立默认的C++项目生成的目录结构是不一样的。如果是C#项目，则解决方案总文件夹下就只包含解决方案配置文件sln和一个项目总文件夹(共两个东东)，而项目总文件夹下包含c#源文件、项目配置文件proj、一个Properties属性文件夹、一个obj文件夹和一个bin文件夹，其中obj和bin文件夹下都包含debug和release两个文件夹。obj文件夹下存放中间编译结果（扩展名更加项目类型而不同），而bin文件夹下存放最终生成的结果（扩展名一般为exe或dll）。

打包dll

如果要打包的函数分布在不同的文件中，在相应的每个头文件和源文件都做如下修改即可。

头文件

1
2
3
4
5
6
7
8
9

#ifdef PREG_API
    #define PREG_API_EXPORT _declspec(dllexport)
#else
    #define PREG_API_EXPORT _declspec(dllimport)
#endif // PREG_API

PREG_API_EXPORT result *my_detect(char *datacfg, char *cfg, network *net, char *filename, float thresh, float hier_thresh, int *objects_num);

PREG_API_EXPORT network *my_load_weight(char *cfgfile, char *weightfile);

源文件

奇异值分解(SVD)原理与在降维中的应用

奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结，并讨论在在PCA降维算法中是如何运用运用SVD的。

回顾特征值和特征向量

我们首先回顾下特征值和特征向量的定义如下：$Ax=\lambda x$

其中A是一个$n \times n$的矩阵，$x$是一个$n$维向量，则我们说$\lambda$是矩阵A的一个特征值，而$x$是矩阵A的特征值$\lambda$所对应的特征向量。

前言

独立同分布i.i.d.

百度百科中解释为：在概率统计理论中，指随机过程中，任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立，那么这些随机变量是独立同分布。如果随机变量X1和X2独立，是指X1的取值不影响X2的取值，X2的取值也不影响X1的取值且随机变量X1和X2服从同一分布，这意味着X1和X2具有相同的分布形状和相同的分布参数，对离随机变量具有相同的分布律，对连续随机变量具有相同的概率密度函数，有着相同的分布函数，相同的期望、方差。如实验条件保持不变，一系列的抛硬币的正反面结果是独立同分布。

关于独立同分布，西瓜书这样解释道：输入空间$X$中的所有样本服从一个隐含未知的分布，训练数据所有样本都是独立地从这个分布上采样而得。

好了，那为啥非要有这个假设呢？

最近学到了PCA，看到了斯坦福大学的教程，特翻译了一下，并加上了一些自己的理解。

主成分分析（PCA）是用来提升无监督特征学习速度的数据降维算法。

假设你正在训练图像，因为图像中相邻图片的元素具有很高的相关性，所以数据是冗余的。假设输入是16x16的灰度图片，则$\textstyle x \in \Re^{256}$。因为相邻元素之间有很高的关联性，所以PCA可以在错误率很小的情况下对数据进行降维。

例子和数学背景

我们使用$n=2$维度的数据$\textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\}$作为输入，则$\textstyle x^{(i)} \in \Re^2$。为了方便解释，我们以二维数据降一维为例（实际应用可能需要把数据从256维降到50维）：

单目定位和双目定位的选择，我觉得主要还是成本和时间的考虑。之前也尝试过双目定位，感觉要更精准些，但双目测距需要对两幅图像进行图像变换和极线匹配，稍微耗时了一些。这几天尝试了一下单摄像头进行测距定位，主要有两个思路：

定位测量插值得到每个像素的实际坐标　　

该方法总觉得有很大的问题：一个是摄像头安装后就必须固定不动，稍微的旋转都会导致之间测量的像素点对应的坐标偏移。另一个是人工测量的工程量之大，对于$10241280$像素的摄像头，准确的测量就应该是130万个点，而就算我们按米来分割地面，$1020m^2$的地面也要测量200个点，就算可以通过算法自动识别，做200个标志就算测量画线也是令人头疼的。考虑到针孔成像模型的等比例放大，我们通过直接打印布满等距阵列圆点的纸来进行测量。

其原理如下：