与原点的最短距离
假如有方程：
图像是这个样子滴：
现在我们想求其上的点与原点的最短距离：
特征值与特征向量(马同学)
（下面的回答只涉及实数范围）。
关于特征值、特征向量可以讲的确实很多，我这里希望可以给大家建立一个直观的印象。
先给一个简短的回答，如果把矩阵看作是运动，对于运动而言，最重要的当然就是运动的速度和方向，那么（我后面会说明一下限制条件）：
- 特征值就是运动的速度
- 特征向量就是运动的方向
既然运动最重要的两方面都被描述了，特征值、特征向量自然可以称为运动（即矩阵）的特征。
注意，由于矩阵是数学概念，非常抽象，所以上面所谓的运动、运动的速度、运动的方向都是广义的，在现实不同的应用中有不同的指代。
函数求导
Markdown公式
如果以下没有你需要的数学公式，你还可以从这里寻找short-cn.pdf
常用语法
| 标志 | 符号 | 显示 |
|---|---|---|
| 上标 | x^y | $x^y$ |
| 下标 | x_y | $x_y$ |
| 四周标注 | \sideset{^1_2}Y{^3_4}Y | $\sideset{^1_2}{^3_4}Y$ |
| 分数 | \frac{1}{x+1} | $\frac{1}{x+1}$ |
| 分数 | 1\over{x+1} | $1\over{x+1}$ |
| 开方 | \sqrt[2]{3} | $\sqrt[2]{3}$ |
| 开方 | \sqrt{3} | $\sqrt{3}$ |
| 省略号(下边) | x_1, x_2, \ldots, x_n | $x_1, x_2, \ldots, x_n$ |
| 省略号(中间) | x_1, x_2, \cdots, x_n | $x_1, x_2, \cdots, x_n$ |
| 矢量 | \vec{a} | $\vec{a}$ |
| 积分 | \int_0^1x{\rm d}x | $\int_0^1x{\rm d}x $ |
| 极限 | \lim_{n\rightarrow0}n | $\lim_{n\rightarrow0}n$ |
| 累加 | \sum_1^n\frac{1}{x} | $\sum_1^n\frac{1}{x}$ |
| 累乘 | \prod_{i=0}^n\frac{1}{x^2} | $\prod_{i=0}^n\frac{1}{x^2}$ |
| 角括号 | \left \langle \frac{a}{b} \right \rangle | $\left \langle \frac{a}{b} \right \rangle$ |
| 空格 | x\ y | $x\ y$ |
| 上下布局 | \underset {\theta }{argmax} | $\underset {\theta }{argmax}$ |
插入公式
LaTeX的数学公式有两种：行中公式和独立公式。行中公式放在文中与其它文字混编，独立公式单独成行。
C检查内存泄露
windows下使用VS
方法一
在主函数最上端加上，否则无法显示行号
1 | #define _CRTDBG_MAP_ALLOC |
然后，在主函数最后一句return 0;前面加上_CrtDumpMemoryLeaks();，注意在debug下运行程序，就会出现在那一行多少字节的错误。
例如：
1 | Detected memory leaks! |
typedef函数指针用法
简单的函数指针的应用
形式：返回类型(*函数名)(参数表)
1 | char (*pFun)(int); |
第一行定义了一个指针变量pFun。首先我们根据前面提到的“形式1”认识到它是一个指向某种函数的指针，这种函数参数是一个int型，返回值是char类型。只有第一句我们还无法使用这个指针，因为我们还未对它进行赋值。
第二行定义了一个函数glFun()。该函数正好是一个以int为参数返回char的函数。我们要从指针的层次上理解函数——函数的函数名实际上就是一个指针，函数名指向该函数的代码在内存中的首地址
C头文件
caffe imcol详解
本文讲解的是caffe中卷积过程，众所周知caffe中卷积采用的是im2col和sgemm的方式。网上已经有很多的im2col的讲解。原本不打算写这篇文章（在此不得不吐槽下，网上有不少的讲解caffe im2col的过程的文章多是错的。一些文章和caffe的具体实现对不上，真不知道他们到底有没有看caffe代码的具体实现，正是因为那些文章，浪费了不少时间。）
本文举例讲解caffe中im2col 和 sgemm的具体过程。在此之前先说明下：caffe中的数据是行优先（row-major）存储的。
im2col
一个图像 input_num=1;
图像通道 input_channel=1;
图像高 input_h=4;
图像宽 input_w=4;
kernel高 kernel_h=3;
kernel宽 kernel_w=3;
stride=1；pad=0；
卷积后，输出图像的计算公式：
output_h=(input_h-kernel_h)/stride+1;
output_w=(input_w-kernel_w)/stride+1;
如下图，（注：图像中数据不代表图像的颜色数值）
矩阵求导法则与性质
首先声明，本篇文章大部分内容来自于网络，具体参考在下面参考小节中给出，我只是将他们进行整理并加上自己的理解。
第一节主要介绍了矩阵向量求导的定义、分子分母布局以及常用的默认布局。第二节主要介绍了如何使用定义法求矩阵向量的导数。第三节主要介绍了如何使用微分法来求解标量对向量的求导，以及标量对矩阵的求导，该节包含了机器学习以及深度学习中的常见的求导过程。第四节主要介绍了矩阵向量求导链式法则，对于推导深度学习中的BP具有很大的帮助。而第五节主要介绍了矩阵对矩阵求导，这部分主要作为扩展内容，在机器学习领域很少用到。最后一节将常用的公式进行了总结，方便查阅。
介绍矩阵求导法则，以及常用的求导公式、迹函数、行列式求导结论。在介绍之前，我们对本文的符号统一一下：
- 对于标量，统一用小写斜体字母表示，例如$f,x,y$
- 对于向量，统一用小写正体字母表示，例如$\mathrm y,\mathrm x$
- 对于矩阵，统一用大写正体字母表示，例如$\mathrm X$，矩阵的大小统一用 $m \times n$表示（$m$行$n$列矩阵）
更进一步，为了便于描述，后面如果没有指明，则求导的自变量用$x$表示标量，$\mathrm{x}$表示n维向量，$\mathrm{X}$表示$m \times n$维度的矩阵，求导的因变量用$y$表示标量，$\mathrm{y}$表示m维向量，$\mathrm{Y}$表示$p \times q$维度的矩阵。
卷积神经网络前向与反向传播
在本文中我们首先对CNN前向传播算法进行总结；接着在基于CNN前向传播算法的基础上，对CNN的反向传播算法做一个总结。在阅读本文前，建议先研究DNN的反向传播算法：这个是一位大佬的博客深度神经网络（DNN）反向传播算法(BP)
回顾CNN的结构
在上一篇里，我们已经讲到了CNN的结构，包括输出层，若干的卷积层+ReLU激活函数，若干的池化层，DNN全连接层，以及最后的用Softmax激活函数的输出层。这里我们用一个彩色的汽车样本的图像识别再从感官上回顾下CNN的结构。图中的CONV即为卷积层，POOL即为池化层，而FC即为DNN全连接层(不管是Pytorch还是TensorFlow全连接层前面必须加上flatten层，变成一维向量)，包括了我们上面最后的用Softmax激活函数的输出层。
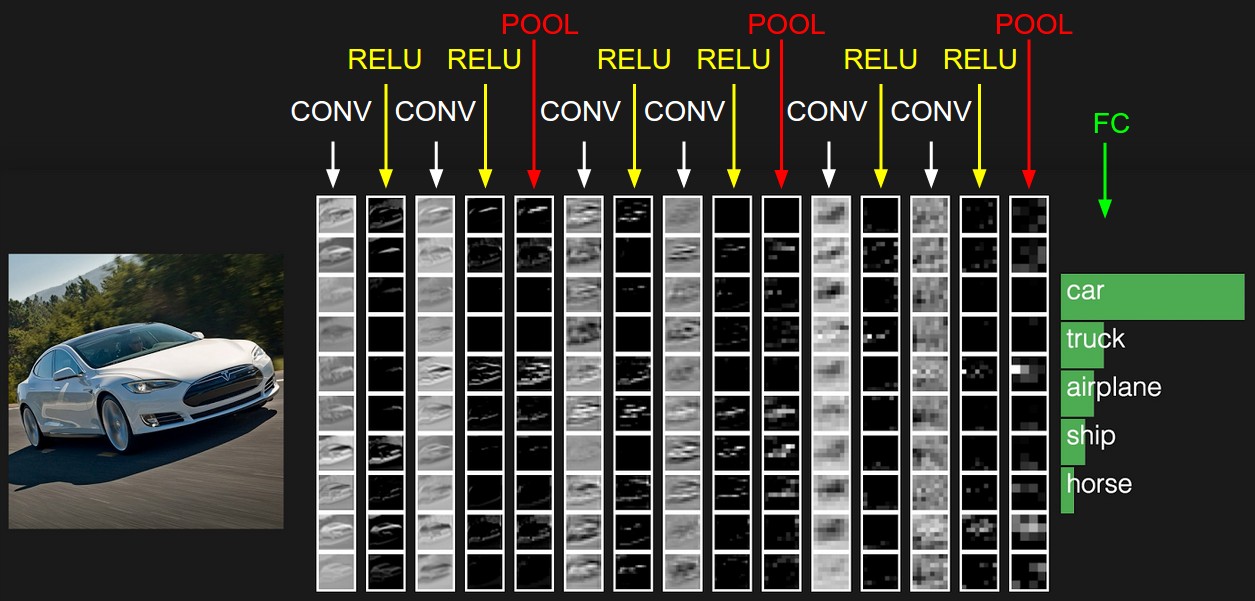
从上图可以看出，要理顺CNN的前向传播算法，重点是输入层的前向传播，卷积层的前向传播以及池化层的前向传播。而DNN全连接层和用Softmax激活函数的输出层的前向传播算法我们在讲DNN时已经讲到了。