zdaiot

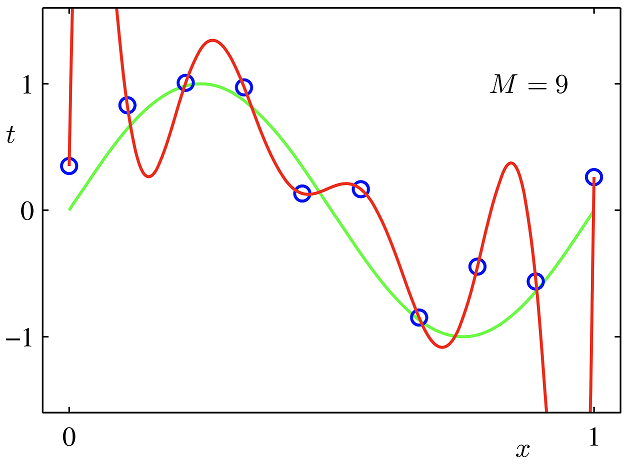
过拟合问题

• 欠拟合：根本原因是特征维度过少，模型过于简单，导致拟合的函数无法满足训练集，误差较大；
  解决方法：增加特征维度，增加训练数据；

• 过拟合：根本原因是特征维度过多，模型假设过于复杂，参数过多，训练数据过少，噪声过多，导致拟合的函数完美的预测训练集，但对新数据的测试集预测结果差。 过度的拟合了训练数据，而没有考虑到泛化能力。
  解决方法：（1）减少特征维度；（2）正则化，降低参数值。

减少过拟合总结：

过拟合主要是有两个原因造成的：数据太少+模型太复杂

（1）获取更多数据 ：从数据源头获取更多数据；

Why & What 正则化

我们总会在各种地方遇到正则化这个看起来很难理解的名词，其实它并没有那么高冷，是很好理解的

首先，从使用正则化解决了一个什么问题的角度来看：正则化是为了防止过拟合， 进而增强泛化能力。用白话文转义，泛化误差（generalization error）= 测试误差（test error），其实就是使用训练数据训练的模型在测试集上的表现（或说性能 performance）好不好

如上图，红色这条“想象力”过于丰富上下横跳的曲线就是过拟合情形。结合上图和正则化的英文 Regularizaiton-Regular-Regularize，直译应该是：规则化（加个“化”字变动词，自豪一下中文还是强）。什么是规则？你妈喊你6点前回家吃饭，这就是规则，一个限制。同理，在这里，规则化就是说给需要训练的目标函数加上一些规则（限制），让他们不要自我膨胀。正则化，看起来，挺不好理解的，追其根源，还是“正则”这两字在中文中实在没有一个直观的对应，如果能翻译成规则化，更好理解。但我们一定要明白，搞学术，概念名词的准确是十分重要，对于一个重要唯一确定的概念，为它安上一个不会产生歧义的名词是必须的，正则化的名称没毛病，只是从如何理解的角度，要灵活和类比。

numpy数据类型转换

numpy数据类型转换需要调用方法astype()，不能直接修改dtype。调用astype返回数据类型修改后的数据，但是源数据的类型不会变，需要进一步对源数据的赋值操作才能改变。例如

1
2
3
4
5
6
7
8
9
10
11
12

>>> a=np.array([1.1, 1.2])
>>> a.dtype
dtype('float64')
>>> a.astype(np.int16)
array([1, 1], dtype=int16)
>>> a.dtype
dtype('float64') #a的数据类型并没有变
>>> a=a.astype(np.int16) #赋值操作后a的数据类型变化
>>> a.dtype
dtype('int16')
>>> a
array([1, 1], dtype=int16)

直接修改dtype数据会强制用新数据类型表示，并没有转换，因此输出错误数据

1
2
3
4
5
6
7
8
9
10

>>> a=np.array([1.1, 1.2])
>>> a.dtype
dtype('float64')
>>> a.dtype=np.int16
>>> a.dtype
dtype('int16') 
>>> a
array([-26214, -26215, -26215,  16369,  13107,  13107,  13107,  16371], dtype=int16)
#原来float64相当于4个int16的位宽，这样强制转换后会将他们直接拆开成4个数，
#因此原来的两个float64成了8个int16

numpy索引

错误使用及结果

笔者最先使用时只是了解到了在tensorflow中tf.layers.batch_normalization这个函数，就在函数中直接将其使用，该函数中有一个参数为training，在训练阶段赋值True，在测试阶段赋值False。但是在训练完成后，出现了奇怪的现象时，在training赋值为True时，测试的正确率正常，但是training赋值为False时，测试正确率就很低。上述错误使用过程可以精简为下列代码段

1
2
3
4
5
6
7
8
9

is_traing = tf.placeholder(dtype=tf.bool)
input = tf.ones([1, 2, 2, 3])
output = tf.layers.batch_normalization(input, training=is_traing)
loss = ...
train_op = optimizer.minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    sess.run(train_op)

batch_normalization

下面首先粗略的介绍一下batch_normalization，这种归一化方法的示意图和算法如下图，

文件相关

输出文件夹所有文件名到txt

若是相对路径

1

ls > filenames.txt

若想包含绝对路径，后面的*.jpg是必须的

在Ubuntu Dash home中创建图标进行快速启动，有两种方法。

第一种方法在.local/share/applications/路径下创建xxx.desktop文件，在此路径下创建的快捷方式只能当前用户可见。一些Appimage创建的快捷启动图标通常放在这里。

第二种方法在/usr/share/applications这个目录，其中存放的全部是所有用户可见的快捷方式。在该目录创建xxx.desktop文件即可。具体操作步骤为：

命令行操作内容：

1
2

cd /usr/share/applications
sudo gedit xxx.desktop

打开需要编辑的文本内容为，将下面中的xxx替换为真实的名字即可。

1
2
3
4
5
6
7
8

[Desktop Entry]
Version=1.0
Name=xxx
Exec=/home/username/xxx.sh
Terminal=false
Icon=/home/username/xxx.png
Type=Application
Categories=Development

矩阵的迹

在线性代数中，n乘n方阵“A”的迹，是指“A”的主对角线各元素的总和（从左上方至右下方的对角线），例如：

其中 $A_{ij}$ 代表在 i 行 j 栏中的数值。同样的，元素的迹是其特征值的总和，使其不变量根据选择的基本准则而定。

迹的英文为“trace”，是来自德文中的“Spur”这个单字（与英文中的“Spoor”是同源词），在数学中，通常简写为“Sp”。

矩阵的迹性质

在神经网络中，激活函数决定来自给定输入集的节点的输出，其中非线性激活函数允许网络复制复杂的非线性行为。正如绝大多数神经网络借助某种形式的梯度下降进行优化，激活函数需要是可微分（或者至少是几乎完全可微分的）。此外，复杂的激活函数也许产生一些梯度消失或爆炸的问题。因此，神经网络倾向于部署若干个特定的激活函数（identity、sigmoid、ReLU 及其变体）。

下面是 26 个激活函数的图示及其一阶导数，图的右侧是一些与神经网络相关的属性。

Step

激活函数 Step 更倾向于理论而不是实际，它模仿了生物神经元要么全有要么全无的属性。它无法应用于神经网络，因为其导数是 0（除了零点导数无定义以外），这意味着基于梯度的优化方法并不可行。

在机器学习里，通常来说我们不能将全部用于数据训练模型，否则我们将没有数据集对该模型进行验证，从而评估我们的模型的预测效果，也就无法从某些候选模型中选择最适合某个学习问题的模型。以多元回归模型为例：$h_\theta(x)=g(\theta_0+\theta_1x+\theta_2x^2+…++\theta_kx^k)$。应该如何确定k的大小，使得该模型对解决相应的分类问题最为有效？如何在偏倚（bias）和方差（variance）之间寻求最佳的平衡点？更进一步，我们同样需要知道如何在加权回归模型中选择适当的波长参数$\Gamma$，或者在基于范式$l_1$的SVM模型中选择适当的参数C？

我们假设模型集合为有限集$\mathcal M=\{M_1,…,M_d\}$我们的目的就是从这d个模型中，选择最有效的模型。

假设样本集为S，根据经验风险最小化原则（ERM），可能会使用这样的算法：

1. 在S上训练每个模型$M_i$，得到相应的假设函数$h_i$；
2. 选择训练误差最小的假设函数，即为我们需要的函数。

然而，这样的算法实际上并不有效。以多元回归模型为例，指数越高，对样本集S的拟合就越准确，这样虽然保证了较低的训练误差，但是这种方法会使泛化误差变得很大，因此，这并不是一个好的方法。

学习率

自适应学习率

在模型的初期的时候，往往设置为较大的学习速率比较好，因为距离极值点比较远，较大的学习速率可以快速靠近极值点；而，后期，由于已经靠近极值点，模型快收敛了，此时，采用较小的学习速率较好，较大的学习速率，容易导致在真实极值点附近来回波动，就是无法抵达极值点。

在tensorflow中，提供了一个较为友好的API, tf.train.exponential_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)，其数学表达式是这样的：

先解释API中的参数的意思，第一个参数learning_rate即初始学习速率，第二个参数，是用来计算步骤的，每调用一次优化器，即自增1，第三个参数decay_steps通常设为一个常数，如数学公式中所示，与第五个参数配合使用效果较好，第五个参数staircase如果设置为True，那么指数部分就会采用整除策略，表示每decay_step，学习速率变为原来的decay_rate，至于第四个参数decay_rate表示的是学习速率的下降倍率。