矩阵的迹
在线性代数中,n乘n方阵“A”的迹,是指“A”的主对角线各元素的总和(从左上方至右下方的对角线),例如:
其中 $A_{ij}$ 代表在 i 行 j 栏中的数值。同样的,元素的迹是其特征值的总和,使其不变量根据选择的基本准则而定。
迹的英文为“trace”,是来自德文中的“Spur”这个单字(与英文中的“Spoor”是同源词),在数学中,通常简写为“Sp”。
矩阵的迹性质
迹是一种线性算子。亦即,对于任两个方阵A、B和标量r,会有下列关系:
因为主对角线不会在转置矩阵中被换掉,所以所有的矩阵和其转置矩阵都会有相同的迹:
设A是一个n×m矩阵,B是个m×n矩阵,则:
其中AB是n×n矩阵,而BA是m×m矩阵。
上述可以由矩阵乘法的定义证明:
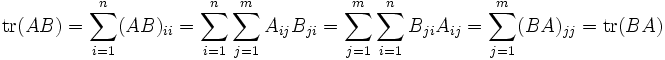
利用这个结果,我们可以推导出方阵的乘积和其任何循环置换的乘积会有相同的迹,称为迹的“循环性质”。例如,有三个方阵A、B、C,则:
更一般化地,当矩阵不被假设为方阵,但其所有乘积依然存在时,其迹依然会完全相同。
若A、B、C为有着相同维度的方阵而且对称的话,其乘积的迹不只在循环置换下不会改变,而是在所有的置换下均不会改变,亦即
迹拥有相似不变性,即$A$和$P^{?1}AP$会有相同的迹,尽管总是存在一相同迹但不相似的矩阵。这一性质可使上面讲过的循环性质来证明:
给定任一线性映射$f : V → V$(V是一有限维向量空间),我们可以定义此一映射的迹为其矩阵表达式的迹,即选定$V$的一基并描述$f$为一对应于此基的矩阵,再取此一方阵的迹。其结果将和所选取的基无关,当不同的基都会得出相似的矩阵。

