最近一直再看复数的一些运算,回宿舍翻书发现这几天拼命在网上所搜索的关于复数的运算以及复数的导数均在大二学的工程数学——《复变函数》中学习过。而且还是我导数教的。呜呜呜,学习的时候不知道学习复变函数有什么用,用的时候才知道。算了废话不多说,开始总结吧。
复数取对数
假设复数为$z=x+iy$,其中$i$表示虚部。假设对$z$取自然对数得到的结果为$a+ib$,则可以得到
根据实部和虚部要分别相等,可以得到:
将上面公式$({2})$中下式除以上式,可以得到$tanb=y/x$,所以$b=arctan(y/x)$。
将上面公式$({2})$中两个式子左右分别平方再相加,可以得到$e^{2a}=x^2+y^2$,即$a=ln\left((x^2+y^2)^{1/2}\right)$。
性质:$log_a MN=log_a M+ log_a N, log_a M^n=nlog_a M$。
所以可以得到最终结果:
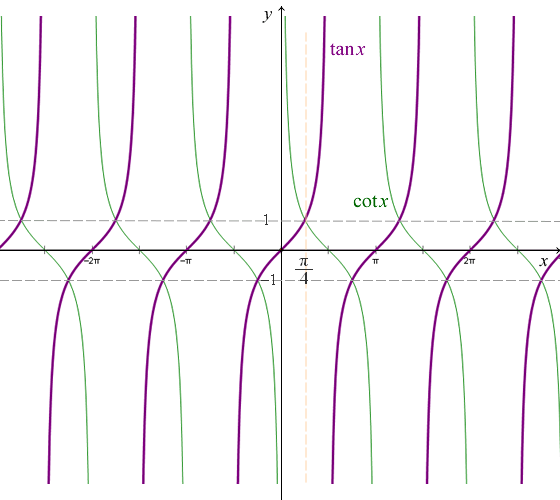
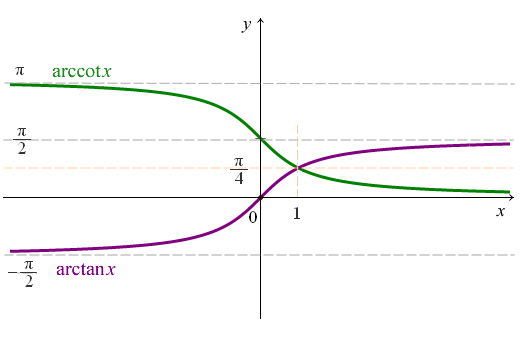
这里,附上$tan \ x$函数和$arctan \ x$的曲线,如下所示,可以看到$arctan \ x$的取值范围在$[-\frac{\pi}{2}, \frac{\pi}{2}]$。
复数矩阵的行列式
其实,复数矩阵的行列式求法和实数矩阵的行列式求法是一致的,我们先看看实数矩阵是如何求行列式的。
对于$2 \times 2$大小的实矩阵,如下所示:
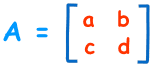
行列式为:

把公式记住的窍门是——十字乘法:
- 蓝色 是 正 (+ad),
- 红色 是 负 (-bc)
对于$3 \times 3$大小的实矩阵,如下所示:
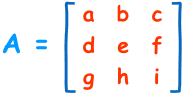
行列式是:
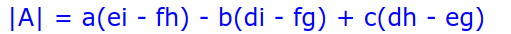
乍看很复杂,但这是有规律的:
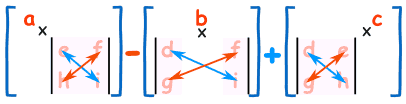
求 3×3 矩阵的行列式:
- 把 a 乘以不在a 的行或列上的 2×2 矩阵的行列式。
- 以 b 和 c 也做相同的计算把结果加在一起,不过 b 前面有个负号!
公式是(记着两边的垂直线|| 代表的行列式)
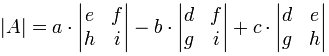
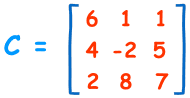

说完实数矩阵的行列式求法,其实复数矩阵的行列式和实数矩阵的行列式公式一样。只不过求实数矩阵的行列式时用的实数相乘,而求复数矩阵的行列式时用的复数相乘。
用MATLAB求复数矩阵行列式的代码以及结果如下:
1 | >> z = [2+3i, 1+5i; 3+2i, 4+4i] |

