函数的极限
函数极限的定义
自变量趋于有限值时函数的极限
定义:设函数$f(x)$在点$x_0$的某个去心邻域内有定义,若$\forall \varepsilon > 0, \exists \delta > 0$,当$0 < |x - x_0| < \delta时,有|f(x) - A| < \varepsilon$,则称常数$A$为函数$f(x)$ 当$x \longrightarrow x_0$时的极限,记作 $\lim_{x \rightarrow x_0}f(x) = A$ 或$f(x) \rightarrow A(当x \rightarrow x_0)$。
上面定义可以简写为:
左极限:$f(x_0^-) = \lim_{x \rightarrow x_0^-}f(x) = A \Longleftrightarrow \forall \varepsilon > 0, \exists \delta > 0, 当x \in (x_0 - \delta, x_0)时,有|f(x) - A| < \varepsilon$
右极限:$f(x_0^+) = \lim_{x \rightarrow x_0^+}f(x) = A \Longleftrightarrow \forall \varepsilon > 0, \exists \delta > 0, 当x \in (x_0, x_0 + \delta)时,有|f(x) - A| < \varepsilon$
定理:函数$f(x)$当$x\rightarrow x_0$时极限存在的充分必要条件是左极限及右极限各自存在并且相等,即
因此,即使$f(x_0^-),f(x_0^+)$都存在,但是两者不相等,极限$\lim_{x\rightarrow x_0} f(x)$也不存在。
例:讨论$x \rightarrow 0 $时$f(x)$的极限是否存在
解:由极限存在的充分必要条件可得:
自变量趋于无穷大时函数的极限
定义:设函数$f(x)$当$|x|$大于某一个整数时有定义, 若$\forall \varepsilon > 0,\exists X > 0$,当$|x| > X$时,有$|f(x) - A| < \varepsilon$, 则称常数$A$为函数$f(x)$当$x \rightarrow \infty$时的极限,记作$\quad \lim_{x \rightarrow \infty}f(x) = A \quad或\quad f(x) \rightarrow A(当x \rightarrow \infty)$
上面定义可以简写为:
函数极限的性质
函数极限的唯一性:如果$\lim_{x\rightarrow x_0} f(x)$存在,那么这极限唯一。
函数极限不存在的常见情况
- 极限为无穷(因此$\infty$放不进实数的数轴上,$+\infty$也就不是一个实数),很好理解,明显与极限存在定义相违;
- 左右极限不相等,例如分段函数;
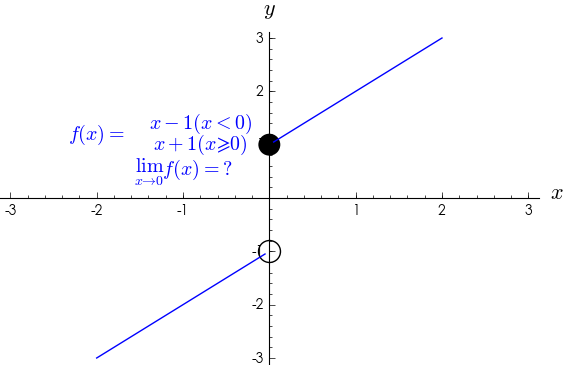
- 没有确定的函数值,例如$sinx$,但要注意,$sinx$是有界的
- 一边存在极限,而另一边不存在
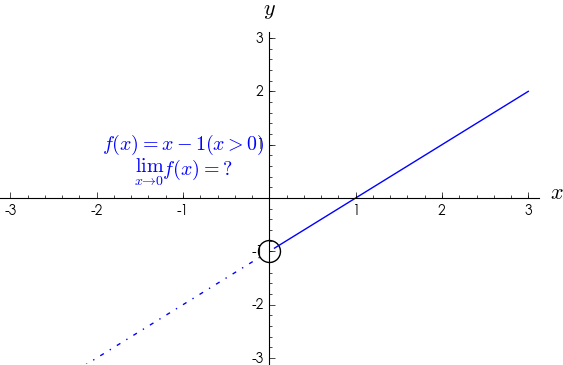
定义:
极限存在的简单理解:如果能够最终 计算出一个值,并且 这个值 不是无穷 ,那么极限就是存在的;
极限不存在的简单理解:如果最终计算不出一个具体的值,或者 结果是 无穷,那么称作极限不存在。

函数的连续性
定义:设函数$y = f(x)$在$x_0$的某邻域内有定义,如果$\lim_{x \rightarrow x_0}{f(x)}$存在,且$\lim_{x \rightarrow x_0}{f(x)} = f(x_0)$,则称函数$f(x)$在$x_0$连续。
可见,函数$f(x)$在点$x_0$连续必须具备下列条件:
1) 函数$f(x)$在点$x_0$有定义,即$f(x_0)$存在;
2) 极限$\lim_{x \rightarrow x_0}{f(x)}$存在;
3) $\lim_{x \rightarrow x_0}{f(x)} = f(x_0)$
4) 连续函数的图像是一条连续而不间断的曲线.
函数的导数
定义:设函数 $y = f(x) $在点$x_0$的某邻域内有定义,若 $\lim_{x \rightarrow x_0}{\dfrac{f(x) - f(x_0)}{x - x_0}} =\lim_{\Delta{x} \rightarrow 0}{\dfrac{\Delta{y}}{\Delta{x}} } = \lim_{\Delta{x} \rightarrow 0} \frac{f(x_0+ \Delta x) - f(x_0)}{\Delta x}$存在,则 称函数$f(x)$在点$x_0$处可导,并称此极限为$y = f(x)$在点$x_0$的导数。记作:$\left. y^\prime \right|_{x = x_0}; f^{\prime}(x_0), \left. \dfrac{dy}{dx}\right|_{x = x_0} 或者\left. \dfrac{df(x)}{dx} \right|_{x = x_0}$
导数的定义是由极限导出的,因此若上面定义的极限不存在,则导函数不存在。
例:证明函数$f(x) = |x|$在$x = 0$不可导.
证:$\because \dfrac{f(0 + h) - f(0)}{h} = \dfrac{|h|}{h} = \left \{ \begin{array}{l} 1, h > 0 \\ -1, h < 0 \end{array} \right.$,$\therefore \lim_{h \rightarrow 0}{\dfrac{f(0 + h) - f(0)}{h}}$不存在,即$|x|$在$x = 0$处不可导.
单侧导数:设函数$y = f(x)$在点$x_0$的某个右${\color{green}{(左)}}$邻域内有定义,若极限$\lim_{\stackrel{\Delta{x} \rightarrow 0^+}{\color{green}{(\Delta{x} \rightarrow 0^-)}}}{\dfrac{\Delta{y}}{\Delta{x}}}= \lim_{\stackrel{\Delta{x} \rightarrow 0^+}{\color{green}{(\Delta{x} \rightarrow 0^-)}}}{\dfrac{f(x_0 + \Delta{x}) - f(x_0)}{\Delta{x}}}$存在,则称此极限值为$f(x)$在$x_0$处的右${\color{green}{(左)}}$导数,记作$f^{\prime}_{\stackrel{+}{\color{green}{(-)}}}(x_0)$。即 $\quad {f^{\prime}}_{\stackrel{+}{\color{green}{(-)}}}{(x_0)} = \lim_{\stackrel{\Delta{x} \rightarrow 0^+}{\color{green}{(\Delta{x} \rightarrow 0^-)}}}{\dfrac{f(x_0 + \Delta{x}) - f(x_0)}{\Delta{x}}}$
定理:函数$ y = f(x) $在点$ x_0$ 可导的充分必要条件是$f^{\prime}_{+}{(x_0)}$与$f^{\prime}_{-}{(x_0)}$存在,且$f^{\prime}_{+}{(x_0)} = f^{\prime}_{-}{(x_0)}$。简写为:$\quad f^{\prime}{(x_0)}$存在$\Longleftrightarrow f^{\prime}_{+}{(x_0)} = f^{\prime}_{-}{(x_0)}$
函数$f(x)$处处可导,那么称该函数可导,其导函数记作$y’,f’(x),\frac{dy}{dx}或\frac{df(x)}{dx}$。定义为:
注意:虽然上式中$x$可以取到函数$f(x)$的任何一个值,但是求极限过程中,$x$是常量,$\Delta x$是变量。
导数的几何意义
$f^{\prime}(x_0) \neq \infty$时,曲线在点$(x_0, y_0)$处的$\color{blue}{切线方程: y - y_0 = f^{\prime}(x_0)(x - x_0)}$。
与切线垂直的直线称为曲线$f(x)$在点$(x_0, y_0)$处的法线,若$f’(x_0)\not=0$,法线的斜率为$-\frac{1}{f’(x_0)}$,从而法线方程为:
常用的导数公式
$(C)^{\prime} = 0; (x^{\mu})^{\prime} = \mu x^{\mu -1}; (\ln x)^{\prime} = \dfrac{1}{x}$
$(\sin x)^{\prime} = \cos x; (\cos x)^{\prime} = - \sin x;$
$(a^x)^{\prime} = a^x \ln a; (e^x)^{\prime} = e^x$
导数与连续
定理:函数$f(x)$在点$x_0$处右(左)导数存在 $\Longrightarrow f(x)$在点$x_0$必右(左)连续。
总结:可导必连续,但连续不一定可导(例如$|x|$)。
判断函数是否可导
$\left \{ \begin{array}{l}不连续,一定不可导. \\ 直接用导数定义; \\ 看左右导数是否存在且相等. \end{array} \right.$
这里判断是函数的导数是否存在,而不是函数某一点的导数是否存在。
微分
引例:一块正方形金属薄片受温度变化的影响,其边长由$x_0$变到$x_0+\Delta{x}$,问此薄片面积改变了多少?
设薄片边长为$x$,面积为$A$,则$A = x^2$,当边长$x_0$取得增量$\Delta{x}$时,面积的增量为:
$\Delta{A} = (x_0 + \Delta{x})^2 - x_0^2 $
$= \quad \color{green}{\begin{matrix} \underbrace{ 2x_0 \Delta{x} } \end{matrix} }\qquad + \qquad \color{blue}{\begin{matrix} \underbrace{ (\Delta{x})^2 } \end{matrix}}$
${\color{green}{关于\Delta{x}的线性主部} } \qquad {\color{blue}{\Delta{x} \rightarrow 0时为高阶无穷小} }$
故$\Delta{A} \approx 2x_0 \Delta{x},2x_0 \Delta{x}$称为函数在$x_0$的微分。
定义:若函数$y = f(x)$ 在点$x_0$的增量可表示为$ \Delta{y} = f(x_0 + \Delta{x}) - f(x_0) = A \Delta{x} + o(\Delta{x})$($A$为不依赖与$\Delta{x}$的常数), 则称函数$ y = f(x)$在点$x_0$处可微,而$A\Delta{x}$称为$f(x)$在点$x_0$的微分,记作$dy$或$df$,即$dy = A \Delta{x}$。还可以得到$\Delta{y} = A\Delta{x} + o(\Delta{x})$当$\Delta{x}$很小的时候,$\Delta{y}=dy$。
通常将自变量$x$的增量$\Delta{x}$称为自变量的微分,记作$dx$,所以$dx = \Delta{x}$,所以函数$y = f(x)$的微分记作:$dy=f’(x)dx$,所以有$\frac{}{dy}{dx} = f’(x)$。也就是函数的微分$dy$与自变量的微分$dx$的商等于该函数的导数,因此导数也称为“微商”。
定理:函数$y = f(x)$在点$x_0$可微的充要条件是$y = f(x)$在点$x_0$处可导,且$A = f^{\prime}(x_0)$,即$dy = f^{\prime}(x_0) \Delta{x}$
$证:必要性\\
已知 y = f(x) 在点x_0可微,则\\
\Delta{y} = f(x_0 + \Delta{x}) - f(x_0) = A \Delta{x} + o(\Delta{x}) \\
\therefore \lim_{\Delta{x} \rightarrow 0}{\dfrac{\Delta{y}}{\Delta{x}}} = \lim_{\Delta{x} \rightarrow 0}(A + \dfrac{o(\Delta{x})}{\Delta{x}}) = A\\
故 y = f(x)在点x_0处可导,且f^{\prime}(x_0) = A\\
\ \\
充分性:\\
已知y = f(x)在点x_0处可导,则\\
\lim_{\Delta{x} \rightarrow 0}{\dfrac{\Delta{y}}{\Delta{x}}} = f^{\prime}(x_0) \\
\because \dfrac{\Delta{y}}{\Delta{x}} = f^{\prime}(x_0) + \alpha (\lim_{\Delta{x} \rightarrow 0}{\alpha} = 0) \\
故\quad \Delta{y} = f^{\prime}(x_0)\Delta{x} + \alpha \Delta{x} = {\begin{matrix} \underbrace{ f^{\prime}(x_0)\Delta{x} } \end{matrix} } + o(\Delta{x}) \\
\qquad \qquad \qquad \qquad \qquad \qquad \qquad 线性主部 \ (f^{\prime}(x_0) \neq 0时) \\
即 dy = f^{\prime}(x_0) \Delta{x} \\
\ \\
说明:\Delta{y} = f^{\prime}(x_0) \Delta{x} + o(\Delta{x}) \\
dy = f^{\prime}(x_0) \Delta{x} \\
当f^{\prime}(x_0) \neq 0时, \\
\lim_{\Delta{x} \rightarrow 0}{\dfrac{\Delta{y}}{dy} = \lim_{\Delta{x} \rightarrow 0}{\dfrac{\Delta{y}}{f^{\prime}(x_0) \Delta{x}}}} \\
= \dfrac{1}{f^{\prime}(x_0)} \lim_{\Delta{x} \rightarrow 0}{\dfrac{\Delta{y}}{\Delta{x}}} = 1 \\
所以 \Delta{x} \rightarrow 0时, \Delta{y} 与 dy是等价无穷小,故当|\Delta{x}|很小时,有近似公式: \\
\Delta{y} \approx dy$
微分的几何意义
切线纵坐标的增量:$dy = A\Delta{x} = f^{\prime}(x_0) \Delta{x}$,又$\Delta{y} = A\Delta{x} + o(\Delta{x})$,所以当$\Delta{x}$很小的时候,$\Delta{y}=dy$。
可微、可导、连续、有界
一元函数

一元函数可微、可导、连续与有界之间均无必然联系:
连续函数可以无界也可以有界,例如函数$f(x)= \tan x$和$f(x) = \sin x$。
不连续的函数可以无界也可以有界。例如:
$f(x) = \left\{ \begin{aligned} f(x) & = -1, x < 0 \\ f(x) & = tan(x), 0 < x \end{aligned} \right.$
和
$f(x) = \left\{ \begin{aligned} f(x) & = 1, x >= 0 \\ f(x) & = -1, x < 0\\ \end{aligned} \right.$
有界函数可以连续,也可以不连续,例如
$f(x)=\sin x$
和
$f(x) = \left\{ \begin{aligned} f(x) & =1, x \geq 0 \\ f(x) & = -1, x < 0 \\ \end{aligned} \right.$
可导可以有界也可以无界,例如$f(x)=\sin x$和$f(x) = \tan x$
有界可导也可以不可导,如函数$f(x) = |x|$在$x=0$处不可导。
多元函数
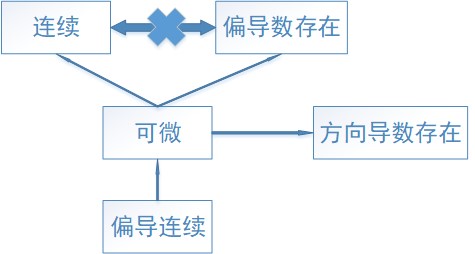
附件
文章中的visio图的附件在这里

