CNN和RNN的不同
在前面我们讲到了DNN,以及DNN的特例CNN的模型和前向反向传播算法,这些算法都是前向反馈的,模型的输出和模型本身没有关联关系。循环神经网络(Recurrent Neural Networks ,以下简称RNN)的输出和模型间有反馈,它广泛的用于自然语言处理中的语音识别,手写书别以及机器翻译等领域。
在前面讲到的DNN和CNN中,训练样本的输入和输出是比较的确定的。但是有一类问题DNN和CNN不好解决,就是训练样本输入是连续的序列,且序列的长短不一,比如基于时间的序列:一段段连续的语音,一段段连续的手写文字。这些序列比较长,且长度不一,比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。
而对于这类问题,RNN则比较的擅长。那么RNN是怎么做到的呢?RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引$\tau$的。对于这其中的任意序列索引号$t$,它对应的输入是对应的样本序列中的$x^{(t)}$。而模型在序列索引号$t$位置的隐藏状态$h^{(t)}$,则由$x^{(t)}$和在$t-1$位置的隐藏状态$h^{(t-1)}$共同决定。在任意序列索引号$t$,我们也有对应的模型预测输出$o^{(t)}$。通过预测输出$o^{(t)}$和训练序列真实输出$y^{(t)}$,以及损失函数$L^{(t)}$,我们就可以用DNN类似的方法来训练模型,接着用来预测测试序列中的一些位置的输出。
Recurrent Neural Networks(RNN)
RNN结构
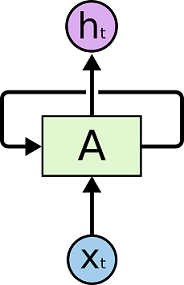
在上面的示例图中,神经网络的模块A,正在读取某个输入$x_i$,并输出一个值$h_i$。循环可以使得信息可以从当前步传递到下一步。RNN 可以被看做是同一神经网络的多次复制,每个神经网络模块会把消息传递给下一个。所以,如果我们将这个循环展开:

RNN结构详细解析
对该结构进行详细解析,如下图所示:

- x代表当前状态下数据的输入,h表示接收到上一节点的输入
- y为当前节点状态下的输出,而h’为传递到下一个节点的输出
- 可以看出输出h’与x和h的值都有关
- y则常常使用h’投入到一个线性层(主要是维度映射),然后使用softmax进行分类得到需要的数据。而一般情况下,如何从h’得到y常常要看具体模型的使用方式。
timesteps和output_dim
以keras深度学习框架为例,调用RNN层的API为
1 | keras.layers.recurrent.SimpleRNN(output_dim, init='glorot_uniform', inner_init='orthogonal', activation='tanh', W_regularizer=None, U_regularizer=None, b_regularizer=None, dropout_W=0.0, dropout_U=0.0) |
输入数据的维度为(batch_size, timesteps, input_dim);如果return_sequences=True,则输出数据的维度为(batch_size, timesteps, output_dim),若return_sequences=False,则输出数据的维度为(batch_size, output_dim)。那么怎么理解输入数据的timesteps和输出维度。
那么怎么理解这里的timesteps和output_dim参数呢?其实,我们之前的图画的不够明确,里面有很多细节都隐藏了,那么真实的图长什么样呢?RecurrentNNs的结构应该这样画,在理解上才会更清晰些,对比MLP,也一目了然。(自己画的为了简约,只画了4个timesteps )
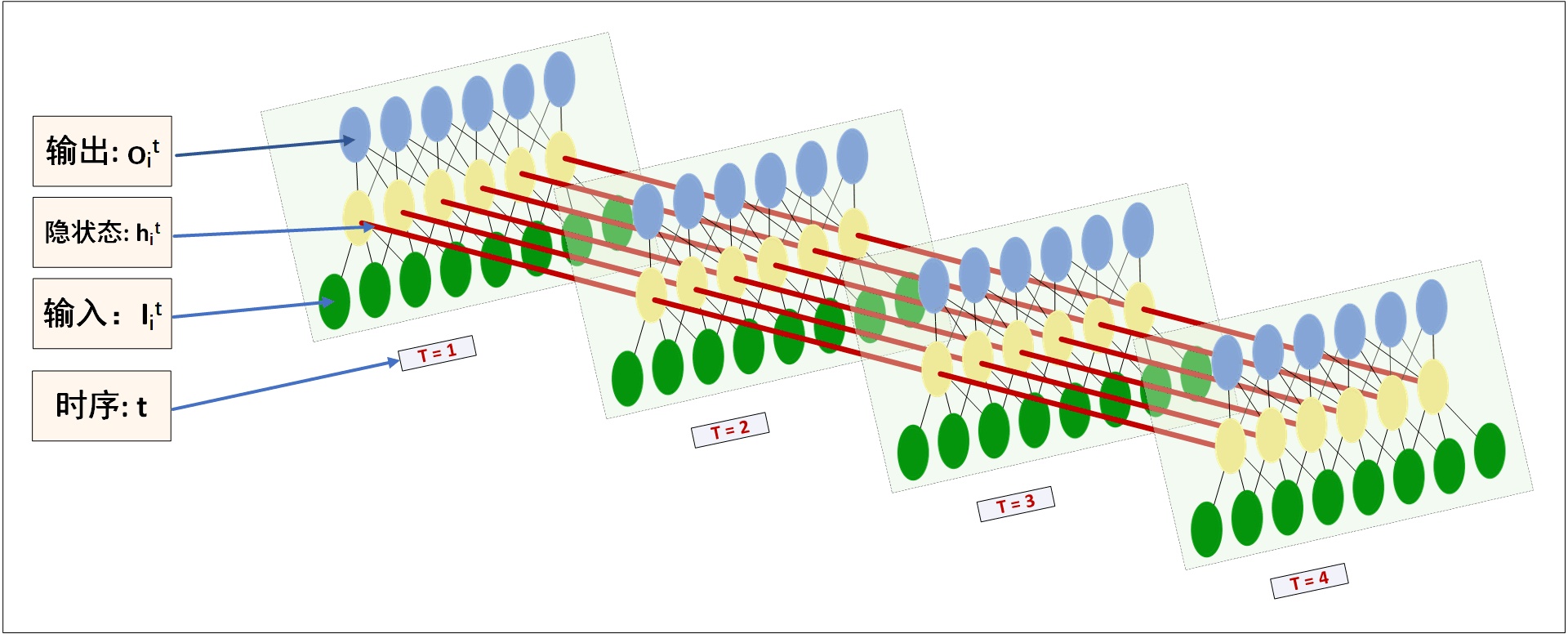
看图。每个时序$t$的输入为$I^{t}$,也就是说一个time_step对应一个输入张量,隐状态$h_{i}^{t}$也就代表了一张MLP的hidden layer的一个cell。输出$o_{i}^{t}$理解无异。以一个具体例子进行说明。
例如有一个样本为hello,而timesteps=4,那么输入为hell的编码,训练目标为llow的编码。对应在图上,就是T=1的时候输入h的编码,目标为l的编码;T=2的时候输入e的编码,目标为l的编码;…;T=4的时候输入l的编码,目标为w的编码。现在固定一个时刻看,以T=1为例,可以看出这就是一个MLP模型,隐状态即为其中的隐层单元,而隐层单元在经过一层网络即可得到输出,而这里所谓的output_dim就是指MLP输出层神经元的数目。不过值得注意的是,从T=1到T=4,共用一个MLP模型,也就是说参数是共享的,这也对应了循环神经网络中时间与循环的概念。
有些时候为了简化处理,会取$o^t=h^t$,即MLP模型只有一层。
长期依赖问题
RNN的关键点之一就是他们可以用来连接先前的信息到当前的任务上,例如使用过去的视频段来推测对当前段的理解。然而RNN要做到这个,还有很多依赖因素。
有时候,我们仅仅需要知道先前的信息来执行当前的任务。例如,我们有一个语言模型用来基于先前的词来预测下一个词。如果我们试着预测 “the clouds are in the sky” 最后的词,我们并不需要任何其他的上下文 —— 因此下一个词很显然就应该是 sky。在这样的场景中,相关的信息和预测的词位置之间的间隔是非常小的,RNN可以学会使用先前的信息。
如下图的不太长的相关信息和位置间隔:

但是同样会有一些更加复杂的场景。假设我们试着去预测“I grew up in France… I speak fluent French”最后的词。当前的信息建议下一个词可能是一种语言的名字,但是如果我们需要弄清楚是什么语言,我们是需要先前提到的离当前位置很远的 France 的上下文的。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。不幸的是,在这个间隔不断增大时,RNN 会丧失学习到连接如此远的信息的能力。
如下图的相当长的相关信息和位置间隔:

理论表明,RNN在训练长序列的时候,会出现梯度消失或梯度爆炸的现象。
Long Short Term(LSTM)
LSTM是一种特殊的RNN,可以解决RNN出现的长期依赖问题。
LSTM结构
LSTM 通过刻意的设计来避免长期依赖问题。记住长期的信息在实践中是 LSTM 的默认行为,而非需要付出很大代价才能获得的能力!
所有 RNN 都具有一种重复神经网络模块的链式的形式。在标准的 RNN 中,这个重复的模块只有一个非常简单的结构,例如一个 tanh 层。
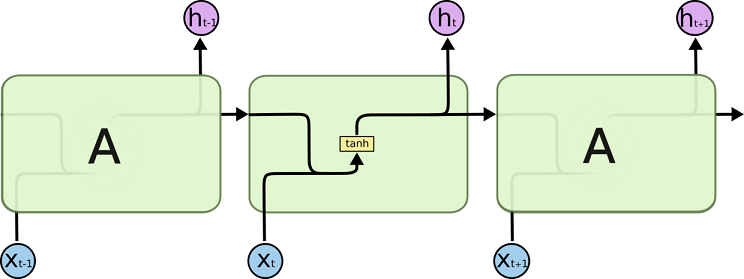
LSTM 同样是这样的结构,但是重复的模块拥有一个不同的结构。不同于单一神经网络层,这里是有四个,以一种非常特殊的方式进行交互。

上述框图中使用的各种元素的图标含义如下:

在上面的图例中,每一条黑线传输着一整个向量,从一个节点的输出到其他节点的输入。粉色的圈代表 pointwise 的操作,诸如向量的和,而黄色的矩阵就是学习到的神经网络层。合在一起的线表示向量的连接,分开的线表示内容被复制,然后分发到不同的位置。
LSTM结构详细解析
核心思想
LSTM 的关键就是细胞状态,水平线在图上方贯穿运行。
细胞状态类似于传送带。直接在整个链上运行,只有一些少量的线性交互。信息在上面流传保持不变会很容易。

门结构
LSTM 有通过精心设计的称作为“门”的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个 sigmoid 神经网络层和一个 pointwise 乘法操作。
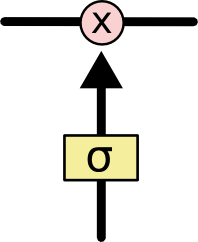
Sigmoid 层输出 0 到 1 之间的数值,描述每个部分有多少量可以通过。0 代表“不许任何量通过”,1 就指“允许任意量通过”!
LSTM 拥有三个门,来保护和控制细胞状态。
忘记阶段
在我们 LSTM 中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为忘记门层完成。该门会读取$h_{t-1}$和$x_t$,输出一个在 0 到 1 之间的数值给每个在细胞状态$C_{t-1}$中的数字。1 表示“完全保留”,0 表示“完全舍弃”。
让我们回到语言模型的例子中来基于已经看到的预测下一个词。在这个问题中,细胞状态可能包含当前主语的性别,因此正确的代词可以被选择出来。当我们看到新的主语,我们希望忘记旧的主语。
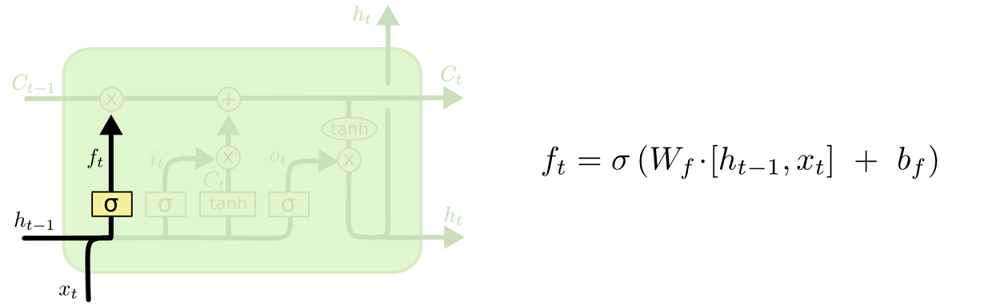
选择记忆阶段
该阶段确定什么样的新信息被存放在细胞状态中。这里包含两个部分。第一,sigmoid 层称 “输入门层” 决定什么值我们将要更新。然后,一个 tanh 层创建一个新的候选值向量$\tilde{C}_t$,会被加入到状态中。下一步,我们会讲这两个信息来产生对状态的更新。
在我们语言模型的例子中,我们希望增加新的主语的性别到细胞状态中,来替代旧的需要忘记的主语。

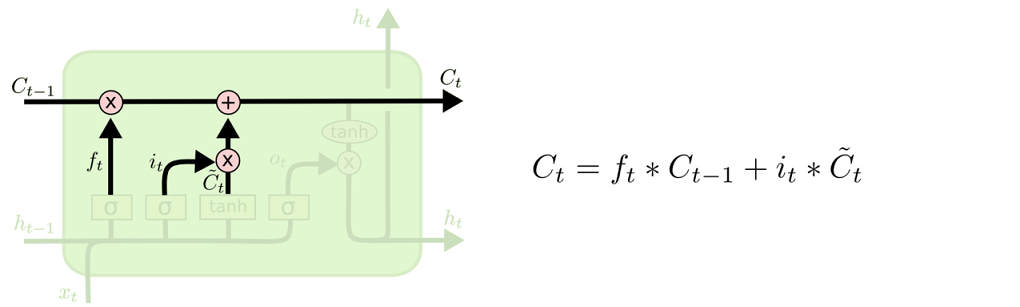
现在是更新旧细胞状态的时间了,$C_{t-1}$更新为$C_t$。前面的步骤已经决定了将会做什么,我们现在就是实际去完成。
我们把旧状态与$f_t$相乘,丢弃掉我们确定需要丢弃的信息。接着加上$i_t * \tilde{C}_t$。这就是新的候选值,根据我们决定更新每个状态的程度进行变化。
在语言模型的例子中,这就是我们实际根据前面确定的目标,丢弃旧代词的性别信息并添加新的信息的地方。
输出阶段
最终,我们需要确定输出什么值。这个输出将会基于我们的细胞状态,但是也是一个过滤后的版本。首先,我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。接着,我们把细胞状态通过 tanh 进行处理(得到一个在 -1 到 1 之间的值)并将它和 sigmoid 门的输出相乘,最终我们仅仅会输出我们确定输出的那部分。
在语言模型的例子中,因为他就看到了一个 代词,可能需要输出与一个 动词 相关的信息。例如,可能输出是否代词是单数还是负数,这样如果是动词的话,我们也知道动词需要进行的词形变化。

LSTM的另一种理解方法
LSTM结构(图右)和普通RNN的主要输入输出区别如下所示。
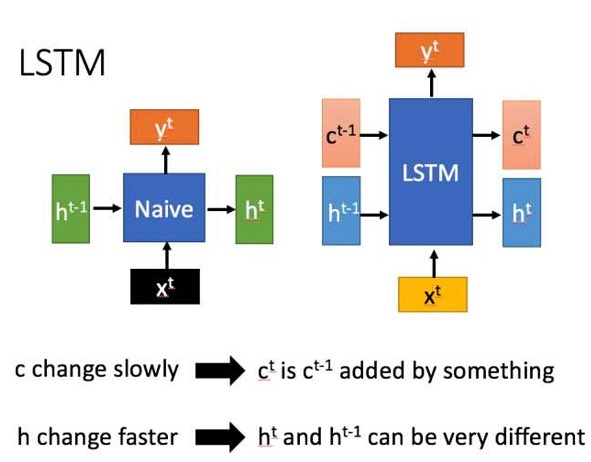
- RNN只有一个传递状态$h_t$,而LSTM有两个传递状态$c_t$(cell state)和$h_t$(hidden state),注意:RNN中的$h_t$对于LSTM的$c_t$
- 对于传递下去的$c_t$改变的很慢,通常$c_t$是上一个状态传来的$c_{t-1}$加上一些数值。
- $h_t$在不同节点下往往有很大的区别
首先使用LSTM的当前输入$x_t$和上一个状态传递下来的$h_{t-1}$拼接训练得到四个状态。
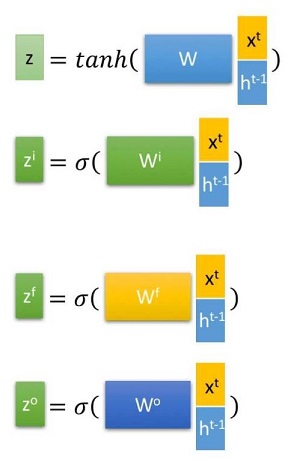
其中,$z^f,z^i,z^o$是由拼接向量乘以权重矩阵之后,再通过一个$sigmoid$激活函数换成0到1之间的数值,来作为一种门控状态。而$z$则是将结果通过一个$tanh$激活函数转换成-1到1之间的值(这里使用$tanh$是因为这里是将其作为输入数据,而不是门控信号)。
下面进一步介绍这四个状态在LSTM内部的使用

LSTM内部主要有三个阶段:
- 忘记阶段。该阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会“忘记不重要的,记住重要的”。具体来说,就是通过计算得到$z^f$(f表示forget)来表示忘记门控,来控制上一个状态的$c^{t-1}$哪些需要留哪些需要遗忘。
- 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行”记忆”。主要是会对输入$x^t$进行选择记忆。哪些重要则着重记录下来,那些不重要,则少记一些。当前的输入内容由前面计算得到的$z$表示。而选择门控信号则是有$z^i$(i表示information)来进行控制。
将上面两步结果相加,即可得到传输给下一个状态的$c_t$。也就是上图中的第一个公式
- 输出阶段。这个阶段将决定哪些将会被当前状态的输出。主要是通过$z^o$进行控制的。并且还对上一阶段得到的$c^o$进行了放缩(通过一个$tanh$激活函数进行变化)。
与普通RNN类似,输出$y^t$往往最终也是通过$h^t$变化得到。
Gate Recurrent Unit(GRU)
GRU(Gate Recurrent Unit)是循环神经网络(Recurrent Neural Network, RNN)的一种。和LSTM(Long-Short Term Memory)一样,也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。
相比LSTM,使用GRU能够达到相当的效果,并且相比之下更容易进行训练,能够很大程度上提高训练效率,因此很多时候会更倾向于使用GRU。
GRU网络结构
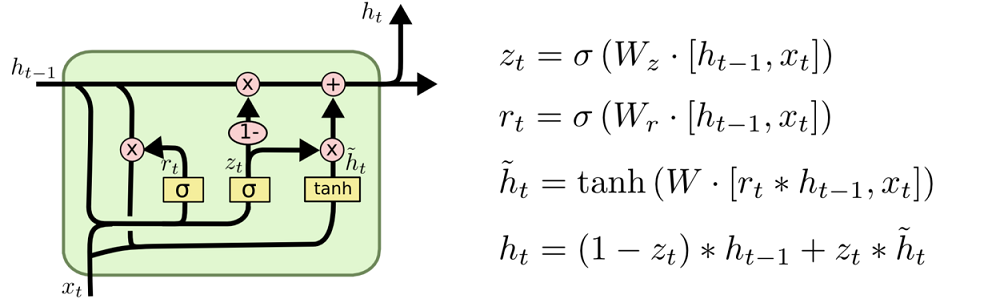
输入输出结构如下:

GRU的输入输出结构与普通的RNN是一样的。有一个当前的输入$x^t$,和上一个节点传下来的隐状态$h^{t-1}$,这个隐状态包含了之前隐节点的相关关系。
结合$x^t$和$h^{t-1}$,GRU会得到当前隐藏节点的输出$y^t$和传递给下一个节点的隐状态$h^t$。
GRU结构详细解析
首先,我们先通过上一个传输下来的状态$h^{t-1}$和当前节点的输入$x^t$来获取两个门控状态。如下图所示。

其中$r$控制重置的门控(reset gate),$z$为控制更新的门控(update gate)。
$\sigma$为sigmoid函数,通过这个函数可以将数据变换为0-1范围内的数值,从而来充当门控信号。
得到门控信号之后,首先使用重置门控来得到”重置”之后的数据$h^{t-1’}=h^{t-1}\bigodot r$,再将$h^{t-1’}$与输入$x^t$进行拼接,再通过一个tanh激活函数来将数据放缩到-1~1的范围内。即得到下图的$h’$

这里的$h’$主要是包含了当前输入的$x^t$数据。有针对性的对$h’$添加到当前的隐藏状态,相当于“记忆了当前时刻的状态”,类似于LSTM的选择记忆阶段。

上图中的$\bigodot$是Hadamard Product,也就是操作矩阵中对应的元素相乘,因此要求两个相乘矩阵是同型的。$\bigoplus$则代表进行矩阵的加法操作。
最后,介绍GRU最关键的一个步骤,称为”更新记忆”阶段。
更新表达式为:$h^t=z\bigodot h^{t-1}+(1-z)\bigodot h’$
首先再次强制一下,门控信号(这里的z)的范围为0~1。门控信号越接近1,代表”记忆”下来的数据越多;而越接近0则代表”遗忘”的越多。
GRU很聪明的一点在于,使用同一个门控$z$就同时可以进行遗忘和选择记忆(LSTM则要使用多个门控)。
- $z\bigodot h^{t-1}$:表示对原本隐藏状态的选择性”遗忘”。这里的z可以想象是遗忘门(forget gate),忘记$h^t$维度中一些不重要的信息。
- $(1-z)\bigodot h’$:表示对包含当前节点信息的$h’$进行选择性”记忆”。与上面类似,这里的$(1-z)$同理会忘记$h’$维度中一些不重要的信息。或者,这里我们更应当看做是对$h’$维度中的某些信息进行选择。
- $h^t=z\bigodot h^{t-1}+(1-z)\bigodot h’$:综上所述,这一步的操作就是忘记传递下来的$h^{t-1}$中的某些维度信息,并加入当前节点输入的某些维度信息。
可以看到,这里的遗忘$z$和选择$(1-z)$是联动的。也就是传递进来的维度信息,我们对进行选择性遗忘,则遗忘了多少权重$z$,我们就会使用包含当前输入的$h’$中所对应的权重进行弥补$1-z$。以保持一种”恒定”状态。
LSTM和GRU的关系
r(reset gate)实际与名字不符。我们这里仅仅使用它来获得了$h’$。
那么,$h’$实际上可以看成对应于LSTM中的hidden state;上一个节点传下来的$h^{t-1}$则对应于LSTM中的cell state。z对应的则是LSTM中的$z^f$ forget gate,那么$(1-z)$似乎是选择门$z^i$了。
LSTM的变体
peephole connection
其中一个流形的 LSTM 变体,就是由 Gers & Schmidhuber (2000) 提出的,增加了 “peephole connection”。是说,我们让 门层 也会接受细胞状态的输入。
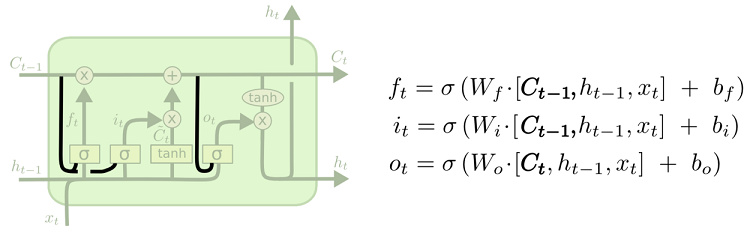
上面的图例中,我们增加了 peephole 到每个门上,但是许多论文会加入部分的 peephole 而非所有都加。
coupled 忘记和输入门
另一个变体是通过使用 coupled 忘记和输入门。不同于之前是分开确定什么忘记和需要添加什么新的信息,这里是一同做出决定。我们仅仅会当我们将要输入在当前位置时忘记。我们仅仅输入新的值到那些我们已经忘记旧的信息的那些状态。
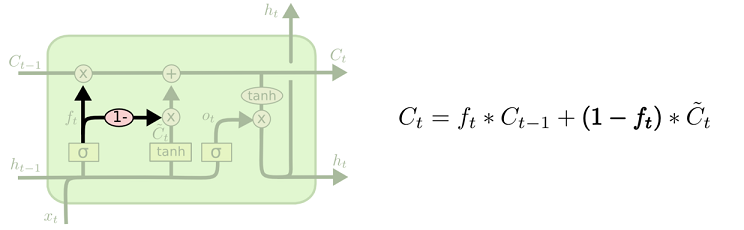
堆叠RNN
堆叠RNN的结构如下所示:
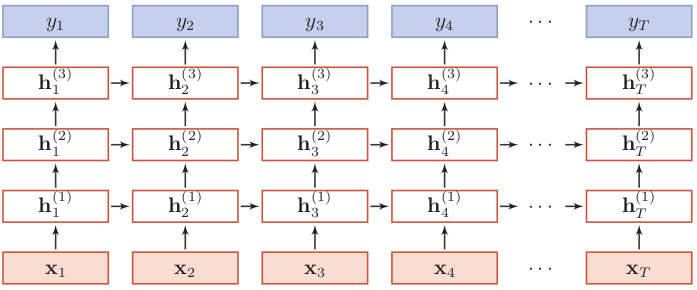
以上是按时间展开的堆叠循环神经网络,横坐标表示不同的时刻,纵坐标表示不同的层。一般的,我们定义 $h_t^{(l)}$为在时刻$t$时第$l$层的隐状态,则它是由时刻$t-1$第$l$层的隐状态与时刻$t$第$l-1$层的隐状态共同决定:
其中$U^{(l)}、W^{(l)}$是权重矩阵,$b^{(l)}$是偏置,$h_t^{(0)} = x_t$。
双向RNN
双向LSTM(Bidirectional Long-Short Term Memorry,Bi-LSTM)不仅能利用到过去的信息,还能捕捉到后续的信息,比如在词性标注问题中,一个词的词性由上下文的词所决定,那么用双向LSTM就可以利用好上下文的信息。双向LSTM由两个信息传递相反的LSTM循环层构成,其中第一层按时间顺序传递信息,第二层按时间逆序传递信息。
为了研究方便,这里以双向RNN结构为例进行介绍,如下图所示。
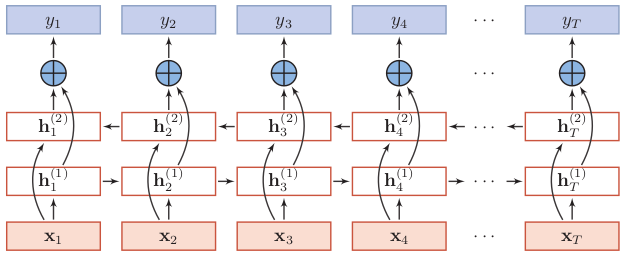
下面来看下隐状态该如何计算,可以看到$t$时刻第一层(顺时间循环层)的隐状态$h_t^{(1)}$取决于前一时刻的隐状态$h_{t-1}^{(1)}$和输入值$x_t$。$t$时刻第二层(逆时间循环层)的隐状态$h_t^{(2)}$取决于下一时刻的隐状态$h_{t+1}^{(2)}$和输入值$x_t$。这与堆叠RNN不同,堆叠RNN除第一层外,其余层的隐状态不由输入值$x_t$直接输入得到,而是取决于前一时刻该层的隐状态和当前时刻前一层的隐状态。
因为模型在训练的时候会将$T$时间序列的数据一起输入到网络中,计算损失并更新参数,所以双向RNN中逆时间循环层可以实现。
双向RNN和堆叠RNN可以结合使用,在顺时间循环层和逆时间循环层可以构造堆叠RNN。
参考
LSTM神经网络输入输出究竟是怎样的? - Scofield的回答 - 知乎
TensorFlow之RNN:堆叠RNN、LSTM、GRU及双向LSTM

