残差网络
1. 神经网络越深越好么?
2014年,GoogleNet和VGGNet在当年的ILSVRC中各自使用深度卷积神经网络取得了优异的成绩,并在分类错误率上优于2012年AlexNet数个百分点。两种结构相较于AlexNet,继续选择了增加网络复杂程度的策略来增强网络的特征表示能力。2015年,何凯明等人使用残差网络ResNet参加了当年的ILSVRC,在图像分类、目标检测等任务中的表现大幅超越前一年的比赛的性能水准,并最终取得冠军。残差网络的明显特征是有着相当深的深度,从32层到152层,其深度远远超过了之前提出的深度网络结构,而后又针对小数据设计了1001层的网络结构。残差网络ResNet的深度惊人,极其深的深度使该网络拥有极强大的表达能力。
因此,可以明显发现,网络的表达能力是随着网络深度的增加而增强的。何恺明等人的实验也证明,时间复杂度相同的两种网络结构,深度较深的网络性能会有相对的提升。
He, Kaiming, and Jian Sun. “Convolutional neural networks at constrained time cost.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015.
然而,网络并非越深越好。计算代价很会大,在网络深度较深时,继续增加层数并不能提高性能,很有可能导致不收敛问题,虽然有一些方法可以弥补,如归一初始化,各层输入归一化,使得可以收敛的网络的深度提升为原来的十倍。然而,虽然收敛了,但网络却开始退化了,即增加网络层数却导致更大的误差,如图1所示。可以看到,在“平整”网络(与本文所介绍的残差网络复杂程度相同,但未使用残差结构的网络)中,随着网络层数的增加,其性能不但没有提升,反而出现了显著的退化。由于训练误差也随着层数增加而提升,所以这个现象可能并非参数的增加造成的过拟合;此外,这个网络在训练时也使用了ReLU激活、BN等手段,一定程度上缓解了梯度消失,这个现象可能也并非完全由梯度消失造成的。这个问题仍有待理论层面的研究和解决。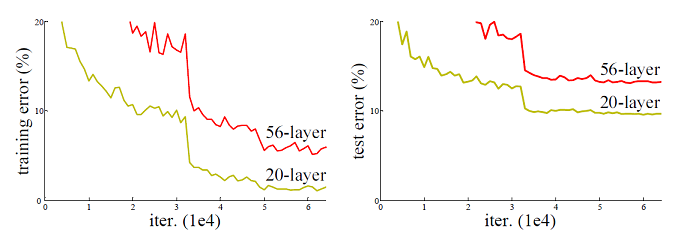
图1使用Cifar-10数据集对“平整”网络进行训练和测试对应的误差
那么没有办法让网络更深了吗?假设上面的实验场景中,多增加的26层全部为单位映射,那么完全可以认为不会产生性能的损失。当然实际应用中这样做是没有意义的,但如果增加的层可以近似为单位映射,或者增加了些许扰动的单位映射,那么就有可能实现上述假设。在这一思路的引导下,深度残差学习(Deep Residual Learning)应运而生。
2. 深度残差网络
ResNet 全称是 Residual Network,每一个节点学到的不再是参数本身,而是残差,这就决定了网络有可能无限加深,基线不变,后面的节点学到的是对前面节点的补充,虽然有震荡,但震荡范围越来越小,直到趋于0。
2.1 残差
残差在数理统计中是指实际观察值与估计值(拟合值)之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话, 我们可以将残差看作误差的观测值。 它应符合模型的假设条件,且具有误差的一些性质。利用残差所提供的信息,来考察模型假设的合理性及数据的可靠性称为残差分析。
2.2 残差函数
resnet学习的是残差函数$F(x)=H(x)-x$,这里如果$F(x)=0$, 那么就是上面提到的恒等映射,事实上,resnet“shortcut connections”中的connections是在恒等映射下的特殊情况,它没有引入额外的参数和计算复杂度。 假如优化目标函数是逼近一个恒等映射, 而不是0映射, 那么学习找到对恒等映射的扰动会比重新学习一个映射函数要容易。从下图可以看出,残差函数一般会有较小的响应波动,表明恒等映射是一个合理的预处理。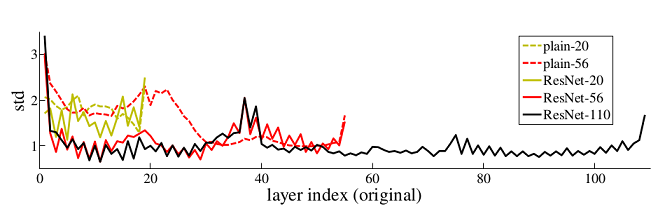
2.3 Residual结构
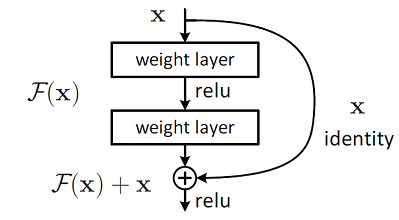
它有二层,如下表达式,其中σ代表非线性函数ReLU
然后通过一个shortcut,和第2个ReLU,获得输出y
当需要对输入和输出维数进行变化时(如改变通道数目),可以在shortcut时对x做一个线性变换Ws,如下式,然而实验证明x已经足够了,不需要再搞个维度变换,除非需求是某个特定维度的输出,如下面的resnet网络结构图中的虚线,是将通道数翻倍。
实验证明,这个残差块往往需要两层以上,单单一层的残差块$(y=W_1x+x)$并不能起到提升作用。
这种残差学习结构可以通过前向神经网络+shortcut连接实现,如结构图所示。而且shortcut连接相当于简单执行了恒等映射,不会产生额外的参数,也不会增加计算复杂度。同时却可以大大增加模型的训练速度、提高训练效果,并且当模型的层数加深时,这个简单的结构能够很好的解决退化问题。 而且,整个网络可以依旧通过端到端的反向传播训练。
shortcut的方式
- 使用恒等映射,如果residual block的输入输出维度不一致,对增加的维度用0来填充;
- 在block输入输出维度一致时使用恒等映射,不一致时使用线性投影以保证维度一致;
- 对于所有的block均使用线性投影。
对这三个选项都进行了实验,发现虽然C的效果好于B的效果好于A的效果,但是差距很小,因此线性投影并不是必需的,而使用0填充时,可以保证模型的复杂度最低,这对于更深的网络是更加有利的。
进一步实验,作者又提出了deeper的residual block:
实际中,考虑计算的成本,对残差块做了计算优化,即将两个3x3的卷积层替换为1x1 + 3x3 + 1x1, 如下图。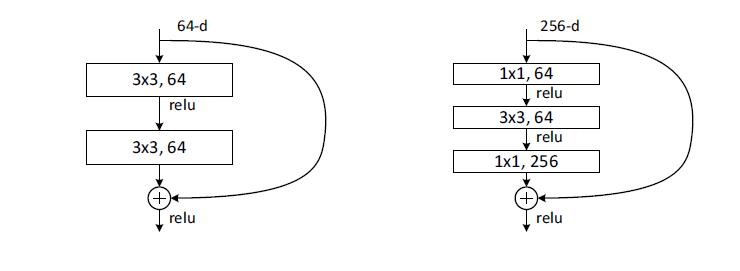
1X1卷积的作用
- 新结构中的中间3x3的卷积层首先在一个降维1x1卷积层下减少了计算,然后在另一个1x1的卷积层下做了还原,既保持了精度又减少了计算量(对于右图,假设不加入1X1的卷积层,参数量为3X3X256X256+3X3X256X256,而加入1X1的卷积之后,参数数量为1X1X256X64+3X3X64X64+1X1X64X64)。
- 另外,1X1的卷积可以实现跨通道的交互和信息整合。CNN里的卷积大都是多通道的feature map和多通道的卷积核之间的操作(输入的多通道的feature map和一组卷积核做卷积求和得到一个输出的feature map),如果使用1x1的卷积核,这个操作实现的就是多个feature map的线性组合,可以实现feature map在通道个数上的变化。接在普通的卷积层的后面,配合激活函数,就可以实现network in network的结构了。
- 还有一个重要的功能,就是可以在保持feature map 尺寸不变(即不损失分辨率)的前提下大幅增加非线性特性,把网络做得很deep。
2.4 残差网络结构
首先构建了一个18层和一个34层的plain网络,即将所有层进行简单的铺叠,然后构建了一个18层和一个34层的residual网络,仅仅是在plain上插入了shortcut,而且这两个网络的参数量、计算量相同,并且和之前有很好效果的VGG-19相比,计算量要小很多。(36亿FLOPs VS 196亿FLOPs,FLOPs即每秒浮点运算次数。)这也是作者反复强调的地方,也是这个模型最大的优势所在(维度匹配的shortcut连接为实线,反之为虚线。维度不匹配时,使用上文中shortcut的方式)。
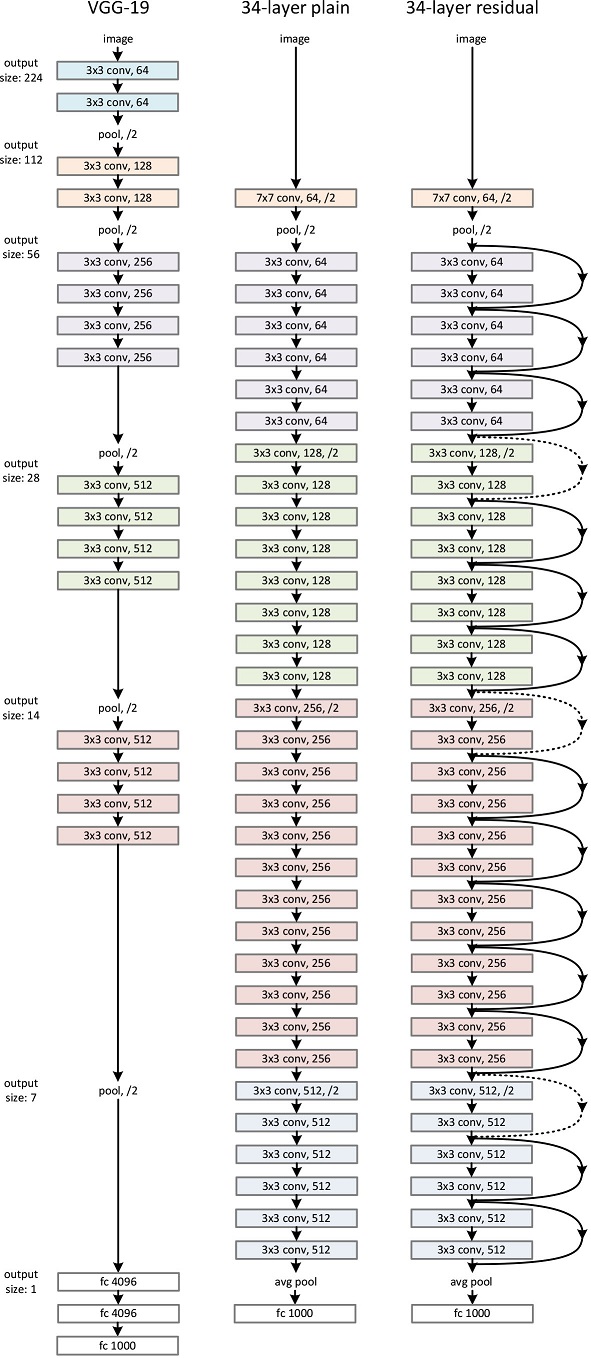
模型构建好后进行实验,在plain上观测到明显的退化现象,而且ResNet上不仅没有退化,34层网络的效果反而比18层的更好,而且不仅如此,ResNet的收敛速度比plain的要快得多。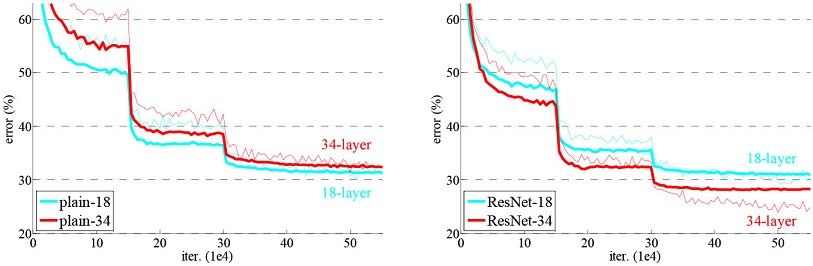
3. 残差网络思考
3.1 为什么同一映射 I(x)=x 这一项前的系数为1而不是1/2。
- 一方面,实践发现机器学习要拟合的(target function)函数 f(x) 经常是很接近同一映射函数的。
- 另一方面,神经网络权值的初始值往往在 0 附近。
因此,以同一映射函数为初始函数,用其他神经网络做微调,相当于赢在了起跑线上。
形象但是松散一点描述就是,经验表明要拟合的函数接近一根直线,于是就用一根直线加一些微小的折线们叠加来拟合。如果只用直线,就成了线性分类/回归,细节难把握;而只用微小的折线们,要优化的路很长,并且还容易过拟合。
有篇文章仔细分析了残差网络背后的原理,简单的说就是大量的(exponential)不同长度的神经网络组成的组合函数(ensemble)
Christian Szegedy, Sergey Ioffe, and Vincent Vanhoucke. Inception-v4, inception-resnet and the impact of residual connections on learning. arXiv preprint arXiv:1602.07261, 2016.
3.2 效果好的解释
- resnet最初的想法是在训练集上,深层网络不应该比浅层网络差,因为只需要深层网络多的那些层做恒等映射就简化为了浅层网络。所以从学习恒等映射这点出发,考虑到网络要学习一个F(x)=x的映射比学习F(x)=0的映射更难,所以可以把网络结构设计成H(x) = F(x) + x,这样就即完成了恒等映射的学习,又降低了学习难度。这里的x是残差结构的输入,F是该层网络学习的映射,H是整个残差结构的输出。
- resnet能有好的表现主要还是因为事物本身的特征就是不同层次的,它等价于多个浅层网络的 ensemble
比如, 区分男女相对比较容易,不需要复杂的计算或者模型(在深度网络中就是网络不需要那么深),但是要区分出范冰冰和张馨予就需要更多的计算了(模型更复杂,网络更深). 我们把网络看成一个映射或者函数,在没有’捷径’(shortcut)的网络里,无论简单还是复杂的特征都得用一个很复杂很深的网络来处理或转换,这似乎有点不合理,而现在resnet引入了捷径,不同层次提取到的特征可以’走捷径’影响预测结果.
在resnet的网络里,我们要区分出李晨,范冰冰和张馨予三个人的思路就是这样的,首先提取区分男女特征,这个特征通过捷径直接影响结果,而更细致的脸型皮肤纹理等等走更细致的网络区分范冰冰和张馨予.
所以shortcut(捷径)这个词用的真是好啊,看似简单的修改,背后蕴含本质的区别.
3.3 为什么要旁路掉 2 层网络才能得到不错的结果?如果只旁路掉 1 层,为什么效果并不好?
不妨看个具体例子,因为一般情况的证明稍后会看到是比较明显的。只需看一个最简单的回归问题,使用 MSE 损失。我们的目标是在 (-3, 3) 区间拟合 sin(x):
方法 1 :
如果用直接的方法:
我们会发现多加几层后就根本无法训练,全部清零。原因很简单,ReLU 会不断丢失信息。当 ReLU 给出 0 之后,后面就全死了。如果网络的层数少,还可以得到这样的结果: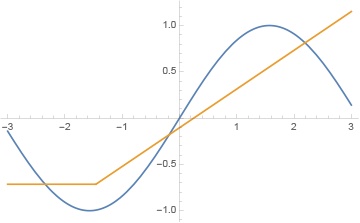
如果层数一多,就肯定全部清零。
方法 2 :
那么加上残差结构吧,比如旁路掉 1 层:
这个肯定也不行。因为 x 只会变大,我们会得到类似这样的结果: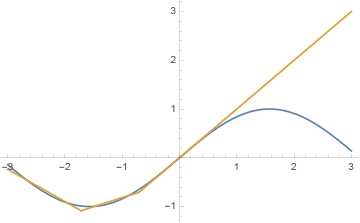
可以用一些办法改善,比如把最后一层的残差和 ReLU 都去掉,但这无疑不是好的办法。
方法 3 :
最简单的解决方法就是旁路掉 2 层。因为如果熟悉 ReLU 就会知道,ReLU 是可以给出负值的,只需要 2 层即可。例如:-Max(0, -x) = Min(0, x)。
于是,最简单的满足我们要求的 2 层结构,就是 Convolution => ReLU => Convolution(这其实就是 1610.02915 PyramidNet 的结构了):
可以得到类似这样的结果: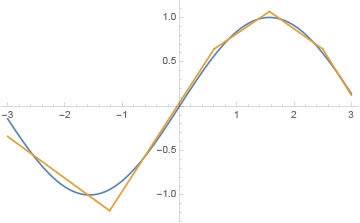
易证这种方法可以拟合任何函数,因为它其实就是在不断”折”一条线。不过,如果层数很多,仍然可能死掉,拟合效果卡住。
方法 4 :
把 ReLU 再换成 leaky 的,例如 PReLU。这就基本解决了死亡问题,可以保证多层训练的效果,例如: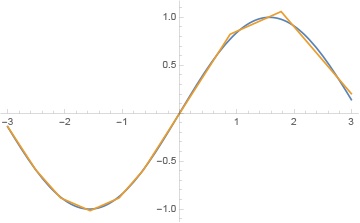
最后,如果我们把方法 1 中的 ReLU 换成 PReLU,是否可以解决死亡问题?遗憾的是不行。这里涉及到数值稳定性。最好的方法仍然是方法 4 的旁路2层残差+PReLU。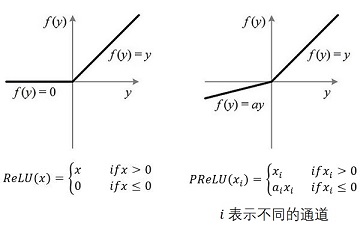
3.4 深层网络容易遇到的问题
- 梯度消失
- 梯度爆炸
- 模型退化(残差结构)
- 参数太多(使用1X1卷积)

