Pytorch基本概念

梯度计算

Variable

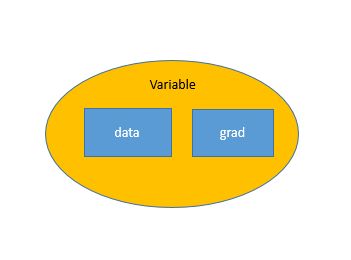
autograd.Variable是torch.autograd中很重要的类。它用来包装Tensor，将Tensor转换为Variable之后，可以装载梯度信息。

Pytorch的一个重要特点就是动态计算图（Dynamic Computational Graphs）。计算图中每一个节点代表一个变量，变量间建立运算关系并且可以修改，而不像Tensorflow中的计算图是固定不可变的。

Variable用来构建一个计算图中的节点。将Tensor转换为Variable类型之后，该Tensor就成了计算图中的一个节点。对于该节点，有两个重要的特性：

• .data——获得该节点的值，即Tensor类型的值
• .grad——获得该节点处的梯度信息

关于Variable的参数之一requires_grad和特性之一grad_fn有要注意的地方，都和该变量是否是人自己创建的有关：

1. requires_grad有两个值：True和False，True代表此变量处需要计算梯度，False代表不需要。变量的requires_grad值是Variable的一个参数，在建立Variable的时候就已经设定好，默认是False。
2. grad_fn的值可以得知该变量是否是一个计算结果，也就是说该变量是不是一个函数的输出值。若是，则grad_fn返回一个与该函数相关的对象，否则是None。

例如下面代码：

import torch
from torch.autograd import Variable

x = Variable(torch.randn(2,2))
y = Variable(torch.randn(2,2))
z = Variable(torch.randn(2,2), requires_grad=True)
a = x + y
b = a + z

以上形成了这样一个计算图：

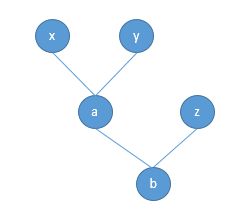
官方文档中所说的“graph leaves”,“leaf variables”，都是指像x,y,z这样的事先创建的、而非运算得到的变量，本文我们把这样的变量称为创建变量，像a,b那样的称为结果变量

• 用户创建变量：x, y, z
• 运算结果变量：a, b

运算结果变量的requires_grad值是取决于输入的变量的，例如变量b：其是由a和z计算得到的，如果a或者z需要计算关于自己的梯度（requires_grad=True），因为梯度要反向传播，那么b的requires_grad就是True；如果a和z的requires_grad都是False那么，b的也是False。

代码如下：

print(x.grad_fn, a.grad_fn)
print(x.requires_grad, y.requires_grad, z.requires_grad)
print(a.requires_grad, b.requires_grad)

运行结果如下：

None None
False False True
False True

可以看出来，因为z的requires_grad为True，所以结果变量b的requires_grad也为True；而因为x、y的requires_grad为False，所以结果变量a的requires_grad也为False。

另外，运算结果变量的requires_grad是不可以更改的，且不会改变。用户创建变量的requires_grad是可以更改的。

代码如下：

x.requires_grad = True
print(a.requires_grad)

运行结果为：

False

可以看出来，因为运算结果变量a的requires_grad已经为False，因此即使后来更改了用户创建变量a的requires_grad，a的requires_grad仍然为False。

而如果强行更改a的requires_grad，结果如下：

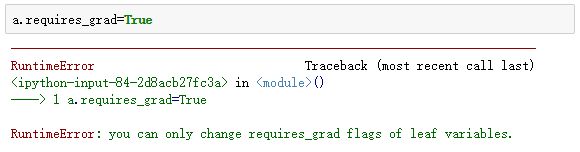
我这里的Pytorch版本为1.3.1，若运行a.requires_grad = True是不会报错，而且a的requires_grad确实已经改变了。

Gradients

我们再来建立一个计算稍微复杂一点能体现出梯度计算过程的计算图：

import torch
from torch.autograd import Variable

x = torch.Tensor([[1.,2.,3.],[4.,5.,6.]])
x = Variable(x,requires_grad=True)
y = x + 2
z = y*y*3
out = z.mean()

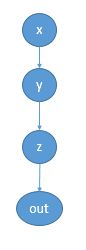
这是这样一个图。先来看一下这四个变量都是什么：

print(x)
print(y)
print(z)
print(out)

运行结果为：

tensor([[1., 2., 3.],
        [4., 5., 6.]], requires_grad=True)
tensor([[3., 4., 5.],
        [6., 7., 8.]], grad_fn=<AddBackward0>)
tensor([[ 27.,  48.,  75.],
        [108., 147., 192.]], grad_fn=<MulBackward0>)
tensor(99.5000, grad_fn=<MeanBackward0>)

我们单独拉出来各个变量的grad_fn：

print(x.grad_fn)
print(y.grad_fn)
print(z.grad_fn)
print(out.grad_fn)

运行结果为：

None
<AddBackward0 object at 0x7f7eef1440f0>
<MulBackward0 object at 0x7f7eef144080>
<MeanBackward0 object at 0x7f7eef1440f0>

可见作为leaf Variable的x，是一个用户创建的变量，它的grad_fn是None。而其余三个变量都是一个运算的结果，其grad_fn是一个与运算对应的对象。

计算图已经构建好了，下面来计算梯度。所计算的梯度都是结果变量关于创建变量的梯度。在这个计算图中，能计算的梯度有三个，分别是out,z和y关于x的梯度，以out关于x的梯度为例：

$$\begin{eqnarray} \frac {\partial out} {\partial x} \end{eqnarray}$$

要在变量out处执行.backward()，这时开始计算梯度，由梯度计算的链式法则算到所有的结果变量（graph leaves），这个图中只有一个x。然后在创建变量处执行.grad，获得结果变量out关于创建变量x的梯度。我们先来手动计算一下：

$$\begin{eqnarray} out = \frac{1}{6} \sum_i z_i \\ z_i = 3(x_i + 2)^2 \end{eqnarray}$$

所以可以得到：

$$\begin{eqnarray} \frac {\partial out} {\partial x_i} = x_i + 2 \end{eqnarray}$$

这时我们就计算出了$\frac {\partial out} {\partial x}$的表达式。在定义x的时候已经给$x_i$赋值了，然后代入表达式中计算，就可以得到一个具体的梯度值。要注意：

• 若是关于”graph leaves“求导的结果变量是一个标量，那么gradient参数是可以缺省的，或者设置gradient参数为None；
• 若是关于”graph leaves“求导的结果变量是一个向量，那么gradient参数是不能缺省的，要是和该向量同维度的tensor

例如out为标量，所以gradient参数是可以缺省的，也可以设置为None

# out为标量，所以`gradient`参数是可以缺省的
out.backward()
# 打印出out关于x的梯度
print(x.grad)

# 运行结果
tensor([[3., 4., 5.],
        [6., 7., 8.]])

# out为标量，所以`gradient`参数可以为None
out.backward(gradient=None)
# 打印出out关于x的梯度
print(x.grad)

# 运行结果
tensor([[3., 4., 5.],
        [6., 7., 8.]])

若是z关于x求导，因为z为向量，那么gradient参数是不能缺省的：

z.backward()

# 运行结果
Traceback (most recent call last):

  File "<ipython-input-3-40c0c9b0bbab>", line 1, in <module>
    z.backward()

  File "/home/zdaiot/miniconda3/lib/python3.7/site-packages/torch/tensor.py", line 166, in backward
    torch.autograd.backward(self, gradient, retain_graph, create_graph)

  File "/home/zdaiot/miniconda3/lib/python3.7/site-packages/torch/autograd/__init__.py", line 93, in backward
    grad_tensors = _make_grads(tensors, grad_tensors)

  File "/home/zdaiot/miniconda3/lib/python3.7/site-packages/torch/autograd/__init__.py", line 34, in _make_grads
    raise RuntimeError("grad can be implicitly created only for scalar outputs")

RuntimeError: grad can be implicitly created only for scalar outputs

此时，正确的写法应该为：

z.backward(gradient=torch.Tensor([[1, 1, 1], [1, 1, 1]]))
# 打印出z关于x的梯度
print(x.grad)

# 运行结果
tensor([[18., 24., 30.],
        [36., 42., 48.]])


z.backward(gradient=torch.Tensor([[0.5, 0.5, 0.5], [0.5, 0.5, 0.5]]))
# 打印出z关于x的梯度
print(x.grad)

# 运行结果
tensor([[ 9., 12., 15.],
        [18., 21., 24.]])

由$z_i = 3(x_i + 2)^2$ ，代入每一个$x_i$，就得到了向量z关于向量x的导数，这个导数是和x同维度的。这种情况需要给出gradient参数，这个参数需要和z同纬度，而且当gradient参数向量所有元素为1.0时，可以得到正确的关于”leaf Variable“的导数。若不为1.0时，算出的导数就扩大对应倍数，这是为什么呢？那这个.backward()括号中的gradient参数到底是干嘛的呢？这篇文章解释了这个原因：

原来在执行z.backward(gradient)的时候，若z不是一个标量，那么就先构造一个标量的值：L = torch.sum(z*gradient)，再关于L对各个“leaf Variable”计算梯度

gradients = torch.Tensor([[1, 1, 1], [1, 1, 1]])
print(z * gradients)

# 输出
tensor([[ 27.,  48.,  75.],
        [108., 147., 192.]], grad_fn=<MulBackward0>)

L = torch.sum(z * gradients)
L.backward()
print(x.grad)

# 输出
tensor([[18., 24., 30.],
        [36., 42., 48.]])

也就是说，若z不是标量，那么就在计算图中添加一个由z运算得到的标量L：

L = torch.sum(z * gradients)

因为要把z和gradients对应元素相乘，于是向量gradients需要和z的维度相同。L.backward()或者说z.backward(gradient=gradients)会计算$\frac{\partial L}{\partial x}$，当gradients参数向量所有元素都为1时，计算出的 x.grad 正是$\frac{\partial z}{\partial x}$ ，因为$\frac{\partial L}{\partial z}=1$。这也是为什么.backward(gradient=...)括号里这个参数名为gradient，因为它是构造出的变量L关于原变量z的梯度。

参考

Autograd:PyTorch中的梯度计算