针孔相机模型
先简单说一下针孔摄像机的原理。成像平面(有的地方也称投影平面)到小孔的距离为焦距$f$,物体到小孔的距离为$Z$,其中物体和投影是倒立相似的关系,下图为针孔摄像机的实际物体投影到成像平面的示意图:
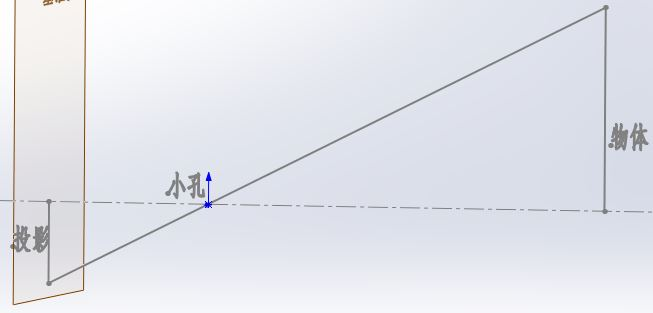
如果按照实际的投影关系建立坐标系,那么投影坐标和物体坐标的符号总是相反的,考虑起来不太方便,于是在“数学上”把成像平面平移到其关于小孔对称的位置,这样投影坐标和物体坐标符号就相同了,示意图如下:
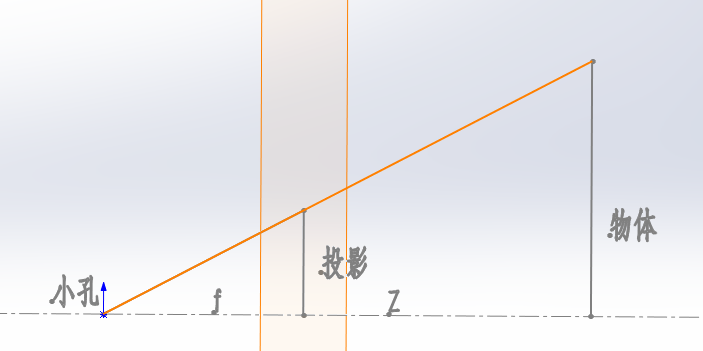
根据三角形相似的原理,可以列出如下等式:
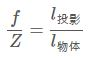
该公式在接下的推导中会用到。
结合以上分析,小孔成像模型如图所示:
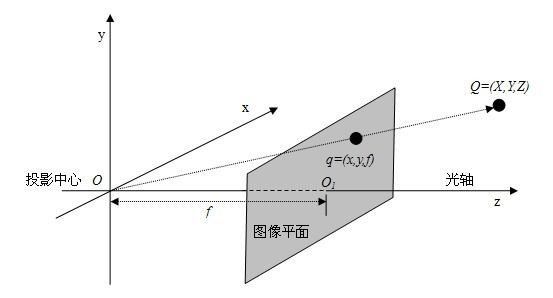
其中:
- O点表示camera centre,即相机的中心点,也是相机坐标系的中心点;
- z轴表示principal axis,即相机的主轴;
- q点所在的平面表示image plane,即相机的像平面,也就是图片坐标系所在的二维平面;
- O1点表示principal point,即主点,主轴与像平面相交的点;
- O点到O1点的距离,也就是右边图中的f,即相机的焦距;
- 像平面上的x和y坐标轴是与相机坐标系上的X和Y坐标轴互相平行的;
- 相机坐标系是以X,Y,Z(大写)三个轴组成的且原点在O点,度量值为米(m);
- 像平面坐标系是以x,y(小写)两个轴组成的且原点在O1点,度量值为米(m);
- 像素坐标系一般指图片相对坐标系,在这里可以认为和像平面坐标系在一个平面上,不过原点是在图片的角上,而且度量值为像素的个数(pixel);
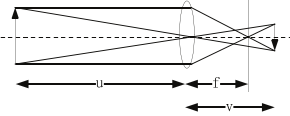
物距u,焦距f,相矩v之间的关系为$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$,如下所示:
坐标系
基本的坐标系:
- 世界坐标系;
- 相机坐标系;
- 成像平面坐标系;
- 像素坐标系
一般来说,标定的过程分为两个部分:
第一步是从世界坐标系转为相机坐标系,这一步是三维点到三维点的转换,包括$R,t$(相机外参,确定了相机在某个三维空间中的位置和朝向)等参数;
第二步是从相机坐标系转为成像平面坐标系,成像平面坐标系转为像素坐标系,这一步是三维点到二维点的转换,包括$K$(相机内参,是对相机物理特性的近似)等参数;
投影矩阵 : $P=K[ R | t ]$是一个3×4矩阵,混合了内参和外参而成。
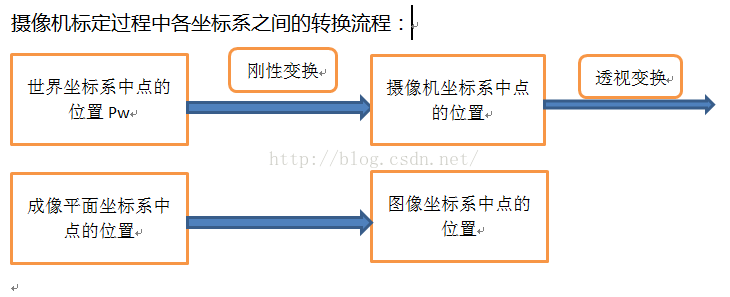
刚体变换(regidbody motion):三维空间中, 当物体不发生形变时,对一个几何物体作旋转, 平移的运动,称之为刚体变换。
透视投影(perspective projection): 用中心投影法将形体投射到投影面上,从而获得的一种较为接近视觉效果的单面投影图。有一点像皮影戏。它符合人们心理习惯,即离视点近的物体大,离视点远的物体小,不平行于成像平面的平行线会相交于消隐点(vanish point)。
相机外参
世界坐标系→相机坐标系
首先,点$Pw$是世界坐标系中的一点。为了将其投影到成像平面上,需要首先将其转换到相机坐标系中。相机坐标系的$X$轴和$Y$轴分别平行于图像的$x$轴和$y$轴,$z$轴垂直与成像平面并且$z$轴的方向的设置将使摄像机前的所有的z坐标为正数。
从世界坐标系到相机坐标系的变换属于刚性变换,也就是平移和旋转组成。因此在世界坐标系中点$Pw$在摄像机坐标系中坐标为$Pc$,他们之间的关系式为:$Pc=R*Pw+T$.其中$T=(Tx,Ty,Tz)$是一个平移向量,这里是将世界坐标系原点坐标平移到摄像机坐标系原点坐标,$R=R(α,β,γ)$是一个旋转矩阵,这个旋转矩阵由三个旋转角度确定,分别是绕摄像机坐标系$z$轴旋转角度$γ$,绕$y$轴旋转角度$β$,绕$x$轴旋转角度$α$:

$R$和$T$中的6个参数$(α,β,γ,Tx,Ty,Tz)$被称为摄像机外参、外方位参数或摄像机位姿。因为他们决定了摄像机坐标系与世界坐标系之间的相对位置关系。
上述公式详细说明如下:
因为世界坐标系和摄像机坐标都是右手坐标系,所以其不会发生形变。我们想把世界坐标系下的坐标转换到摄像机坐标下的坐标,如下图所示,可以通过刚体变换的方式。空间中一个坐标系,总可以通过刚体变换转换到另外一个个坐标系的。转一转,走一走,就到另外一个坐标系下了。
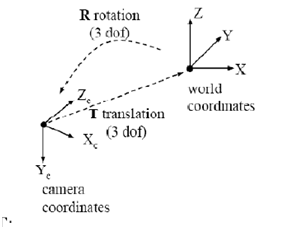
式子$R=R(α,β,γ)$ 则为分别绕XYZ三轴旋转的效果之和。如下面所示:
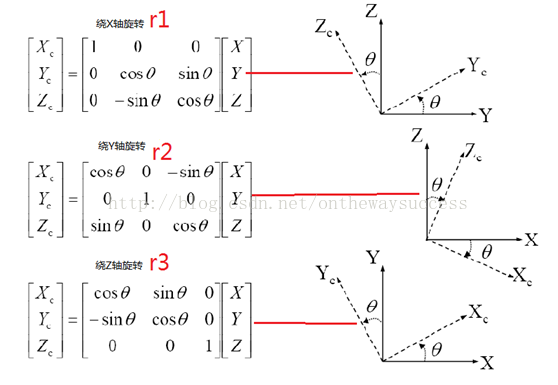
$R=R(α,β,γ)=r1r2r3$.其由三个方向的θ控制,故具有三个自由度。
相机内参
相机坐标系→成像平面坐标系
以$O$点为原点建立相机坐标系。点$Q(X,Y,Z)$为相机坐标系空间中的一点,该点被光线投影到成像图像平面上的$q(x,y,f)$点。
这里将成像平面平移到其关于小孔对称的位置,这样成像坐标和物体坐标符号就相同了
图像平面与光轴z轴垂直,和投影中心距离为f (f是相机的焦距)。按照三角比例关系可以得出:
以上将坐标为(X,Y,Z)的Q点映射到投影平面上坐标为(x,y)的q点的过程称作投影变换。
上述Q点到q点的变换关系用3*3的矩阵可表示为:$q = MQ$ ,其中
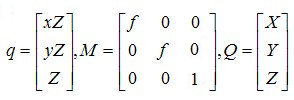
展开上述其中一项,如$xZ=fX$,更加容易理解。
最终得出透视投影变换矩阵为,将下面式子记做式子(1):
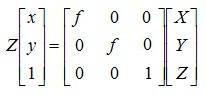
M称为摄像机的内参数矩阵,单位均为物理尺寸。
在这里,$Z$维度已经成为了固定值。因此,完成了三维点到二维点的转换。
通过上面,可以把相机坐标系转换到像图像坐标系的物理单位,$(X,Y,Z)→(x,y)$
成像平面坐标系→像素坐标系
通过下面,可以把成像平面坐标系物理单位映射到到像素坐标系中的像素单位,即$(x,y)→(u,v)$
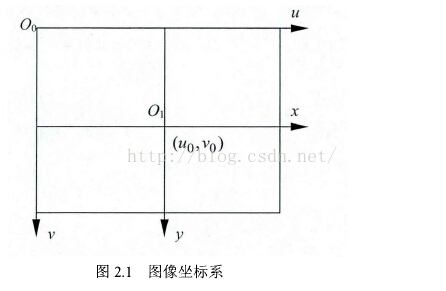
像素坐标系以图像左上角为原点,以像素为单位。即$u-v$坐标系;
成像平面坐标系:以图像平面与光轴的交点$O_1$为原点建立坐标系,水平向右为$x$轴,垂直向下为$y$轴。原点$O_1$一般位于图像中心处,即$x-y$坐标系。$O_1$在以像素为单位的成像平面坐标系中的坐标为$(u_0, v_0)$。
像成像平面坐标系和像素坐标系虽然在同一个平面上,但是原点并不是同一个。
映射关系如下所示:
设每个像素的物理尺寸大小为$dx*dy(mm)$ (由于单个像素点投影在图像平面上是矩形而不是正方形,因此可能$dx != dy$)。
图像平面上某点在成像平面坐标系中的坐标为(x, y),在像素坐标系中的坐标为(u, v),则二者满足如下关系:即$(x,y)→(u,v)$
用齐次坐标与矩阵形式表示为:
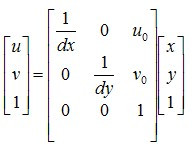
将等式两边都乘以点Q(X,Y,Z)坐标中的Z可得:
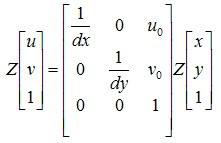
将相机坐标系→成像平面坐标系最终得到的透视投影变换矩阵(1)代入上式可得:
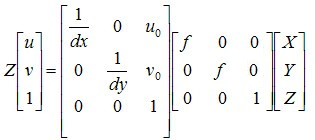
则右边第一个矩阵和第二个矩阵的乘积亦为摄像机的内参数矩阵(单位为像素),相乘后可得,将下式记做式子(2):
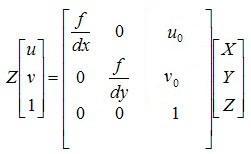
和式子(1)相比,此内参数矩阵中$\frac{f}{dx}, \frac{f}{dy},u_0, v_0$的单位均为像素。令内参数矩阵为K,则上式可写成如下形式,记住式子(3):
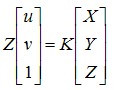
相机内参K
在计算机视觉中,摄像机内参数矩阵:
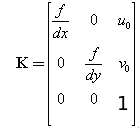
其中$f$为摄像机的焦距,单位一般是mm;$dx,dy$为像元尺寸;$u_0,v_0$为图像中心。$fx = \frac{f}{dx}, fy = \frac{f}{dy}$,分别称为$x$轴和$y$轴上的归一化焦距.
为更好的理解,现以NiKon D700相机为例进行求解其内参数矩阵:
焦距 f = 35mm 最高分辨率:4256×2832 传感器尺寸:36.0×23.9 mm
根据以上定义可以有:
分辨率可以从显示分辨率与图像分辨率两个方向来分类。
- 显示分辨率(屏幕分辨率)是屏幕图像的精密度,是指显示器所能显示的像素有多少。由于屏幕上的点、线和面都是由像素组成的,显示器可显示的像素越多,画面就越精细,同样的屏幕区域内能显示的信息也越多,所以分辨率是个非常重要的性能指标之一。可以把整个图像想象成是一个大型的棋盘,而分辨率的表示方式就是所有经线和纬线交叉点的数目。显示分辨率一定的情况下,显示屏越小图像越清晰,反之,显示屏大小固定时,显示分辨率越高图像越清晰。
- 图像分辨率则是单位英寸中所包含的像素点数,其定义更趋近于分辨率本身的定义。
畸变参数(与点集如何畸变的2D几何相关)
采用理想针孔模型,由于通过针孔的光线少,摄像机曝光太慢,在实际使用中均采用透镜,可以使图像生成迅速,但代价是引入了畸变。
纠正畸变的过程是在
成像平面坐标系→成像平面坐标系之间,即得到相机坐标系在成像平面坐标系的变换后,在成像平面坐标系内部进行的变换。
有两种畸变对投影图像影响较大: 径向畸变和切向畸变。
径向畸变
对某些透镜,光线在远离透镜中心的地方比靠近中心的地方更加弯曲,产生“筒形”或“鱼眼”现象,称为径向畸变。
一般来讲,成像仪中心的径向畸变为0,越向边缘移动,畸变越严重。不过径向畸变可以通过下面的泰勒级数展开式来校正:
这里$(x, y)$是畸变点在成像仪上的原始位置,$r$为该点距离成像仪中心的距离,$(xcorrected ,ycorrected)$是校正后的新位置。
对于一般的摄像机校正,通常使用泰勒级数中的前两项$k_1$和$k_2$就够了;对畸变很大的摄像机,比如鱼眼透镜,可以使用第三径向畸变项$k_3$
切向畸变
当成像仪被粘贴在摄像机的时候,由于透镜制造上的缺陷使得透镜本身与图像平面不平行,会存在一定的误差,使得图像平面和透镜不完全平行,从而产生切向畸变。也就是说,如果一个矩形被投影到成像仪上时,可能会变成一个梯形。切向畸变可以通过如下公式来校正:
这里$(x, y)$是畸变点在成像仪上的原始位置,r为该点距离成像仪中心的距离,$(xcorrected ,ycorrected)$是校正后的新位置。
总结
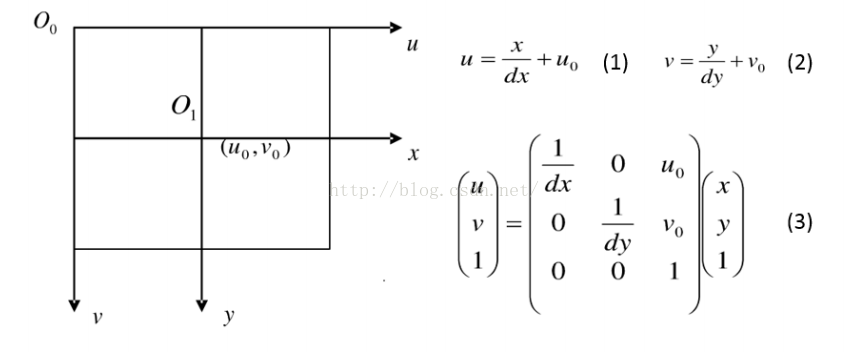
成像坐标系和像素坐标系,成像坐标系原点O1和像素坐标系原点O0有一定的偏差,由此我们建立了等式(1)和(2),可以用矩阵形式(3)表示。:
相机坐标系(C)和世界坐标系(W):
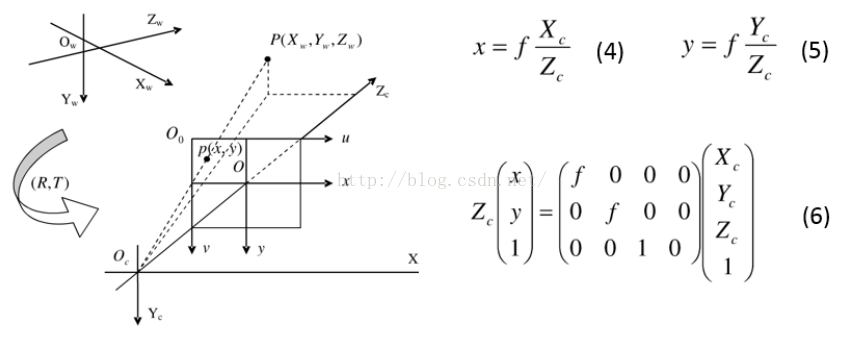
通过相机与图像的投影关系,我们得到了等式(4)和等式(5),可以用矩阵形式(6)表示。我们又知道相机坐标系和世界坐标的关系可以用等式(7)表示:

由等式(3),等式(6)和等式(7)我们可以推导出像素坐标系和世界坐标系的关系:
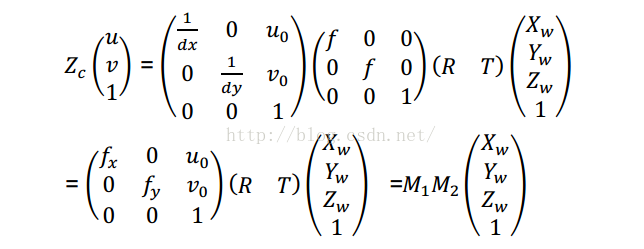
其中$M1$称为相机的内参矩阵,包含内参$(fx,fy,u_0,v_0)$。$M2$称为相机的外参矩阵,包含外参($R$:旋转矩阵,$T$:平移矩阵)。
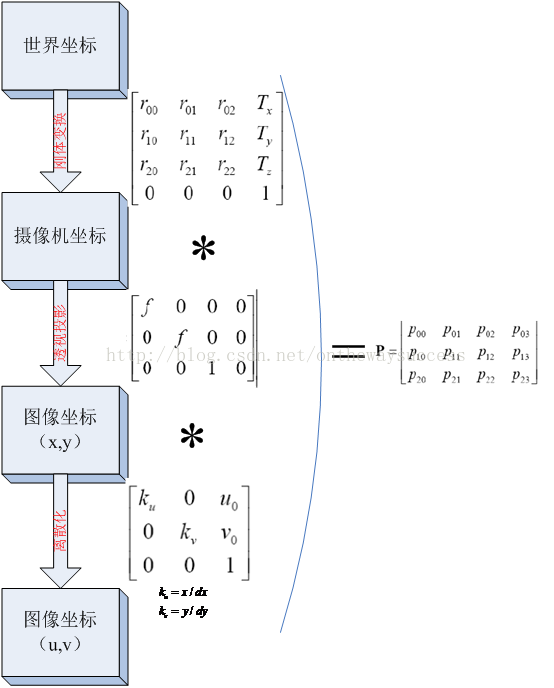
将上述过程用图表示,如下所示,除去齐次坐标控制位P23,P具有11个自由度。
参考
相机标定原理介绍(一)
摄像机成像模型
摄像机标定终极总结版02
关于OpenCV的那些事——相机标定
世界坐标系和相机坐标系,图像坐标系的关系

