单目摄像头距离估计

单目定位和双目定位的选择，我觉得主要还是成本和时间的考虑。之前也尝试过双目定位，感觉要更精准些，但双目测距需要对两幅图像进行图像变换和极线匹配，稍微耗时了一些。这几天尝试了一下单摄像头进行测距定位，主要有两个思路：

定位测量插值得到每个像素的实际坐标　　

该方法总觉得有很大的问题：一个是摄像头安装后就必须固定不动，稍微的旋转都会导致之间测量的像素点对应的坐标偏移。另一个是人工测量的工程量之大，对于$10241280$像素的摄像头，准确的测量就应该是130万个点，而就算我们按米来分割地面，$1020m^2$的地面也要测量200个点，就算可以通过算法自动识别，做200个标志就算测量画线也是令人头疼的。考虑到针孔成像模型的等比例放大，我们通过直接打印布满等距阵列圆点的纸来进行测量。

其原理如下：

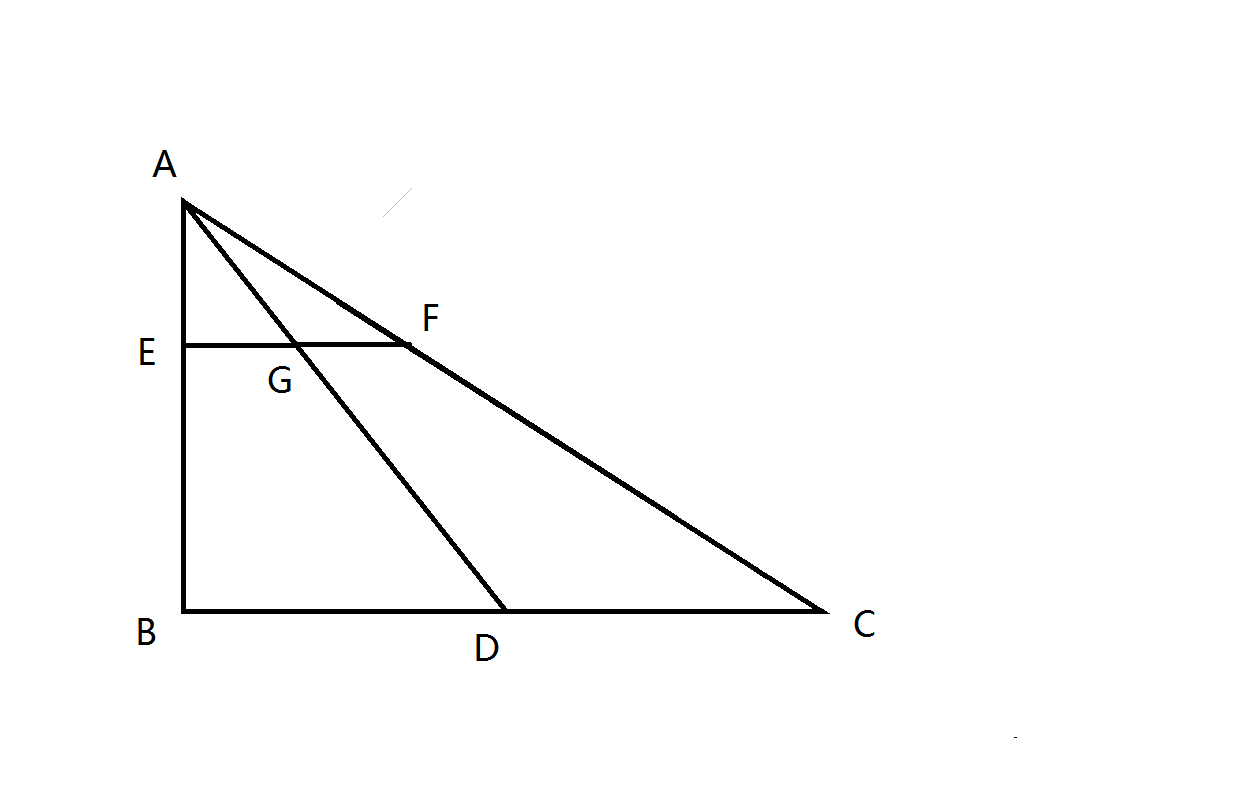
根据相似三角形的等比例关系，有:

$$\frac{EG}{BD}=\frac{AG}{AD} \\ \frac{GF}{DC}=\frac{AG}{AD}$$

同时又有：

$$\frac{EG}{EB}=\frac{AE}{AB}$$　 通过等式传递有： $$\frac{EG}{BD}=\frac{GF}{DC}=\frac{AE}{AB}$$

如此一来，可以在较高距离测量等距阵列点（如标定板），经过插值，再进行等比例放大即可得到每个像素点对应的实际地面的坐标。
　　
处理的示意图如下：

这样操作可以省去人工在地面测量绘画标志。测量好纸上的点距后再进行H/h的放大就可以得到像素对应实际地面的坐标。但实际操作过程中遇到的问题是图像上边缘的梯形失真过于严重，导致打印纸上的标志点不容易识别，因此还需要准备不同距离的等距阵列圆点图。

根据相似三角比例计算出对应像素点的实际坐标　　

这个方法对摄像机标定的要求比较高，同时要求镜头本身造成的畸变就比较小，但总体来说这种方法的可移植性和实用性都较强。其主要的思路还是小孔成像的模型。

模型一：假设测量的点都在Y轴上，此时无X轴分量

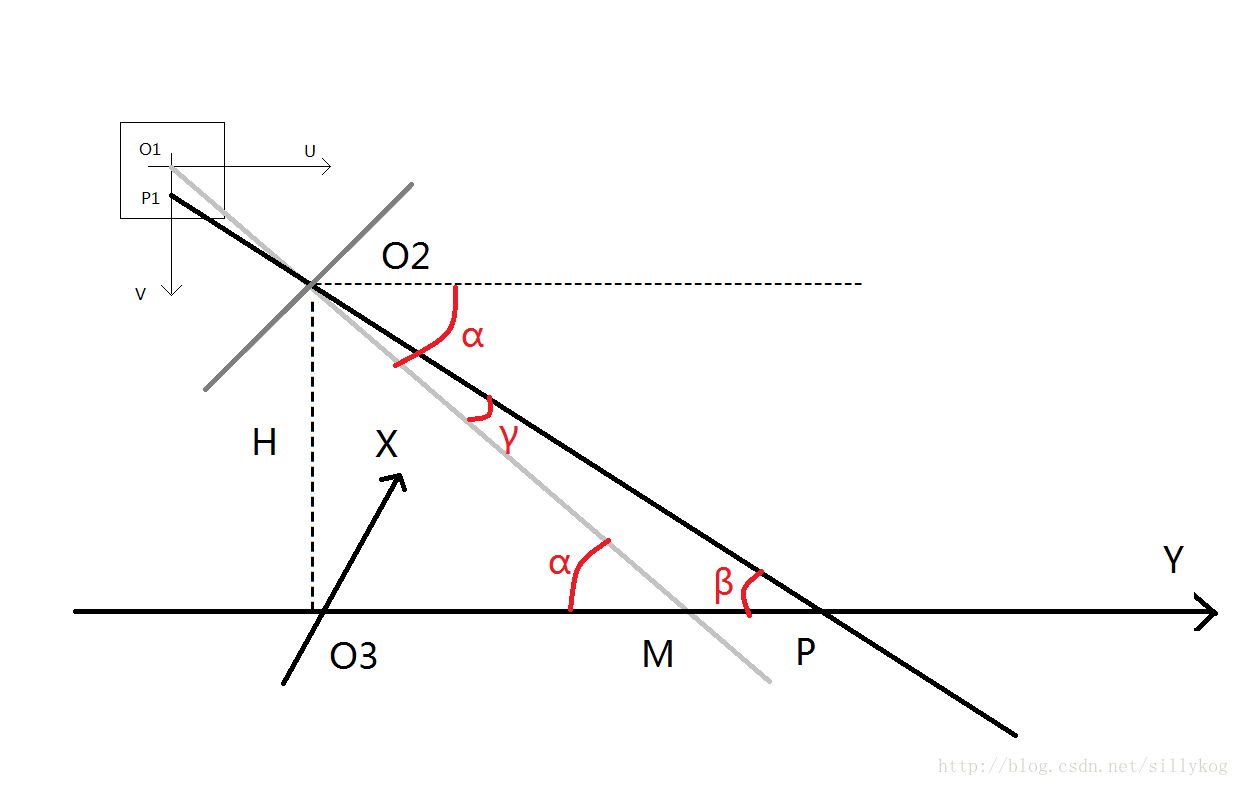
该图主要有三个坐标系，分别是图像坐标系$UO_1V$，以$O_2$为原点的摄像机坐标系，世界坐标系$XO_3Y$（相关的内容我就不复述了，不懂的百度和知乎上都有，搜搜相机标定的知识）

我们可以看到，世界坐标中的点通过光轴成像在图像坐标的点是成比例的，其比例媒介就是相机镜头中心在图像上的像素点$O1$与其在世界坐标中的实际点$M$，通过推导可以求解$O_3P$的长度。（注意，由于相机安装一般都有误差，所以镜头中心点不一定是图像的中点，所以$ucenter，vcenter$不一定为0）　

一步步推导如下：
已知量：

• 摄像机高度H
• 图像坐标中心对应的世界坐标点与摄像头在y轴上的距离$O_3M$
• 镜头中心点的图像坐标$(ucenter，vcenter)$
• 测量像素点的图像坐标$P_1(u,0)$　　　　　　
• 实际像素的长度$xpix$
• 实际像素的宽度$ypix$。
• 摄像头焦距$f$

镜头中心点图像坐标，焦距，像素长宽都可以由标定直接求解出来，通过halcon的标定助手可以很容易的得到，openCV也有相应的程序）

$${ \alpha = \arctan \left( \frac { H } {O_3M} \right) } \\ { \gamma = \arctan \left( \frac { O _ { 1 } P _ { 1 } \times y p i x } { f } \right) = \frac { ( v - v c e n t e r ) * y p i x } { f } } \\ { \beta = \alpha - \gamma } \\ { O _ { 3 } P = \frac { H } { \tan ( \beta ) } }$$

这样就可以得到垂直方向的坐标：$Y=O_3P$

模型二：假设测量的点有X轴、Y轴分量　　

针对以下模型图我们将进行说明：

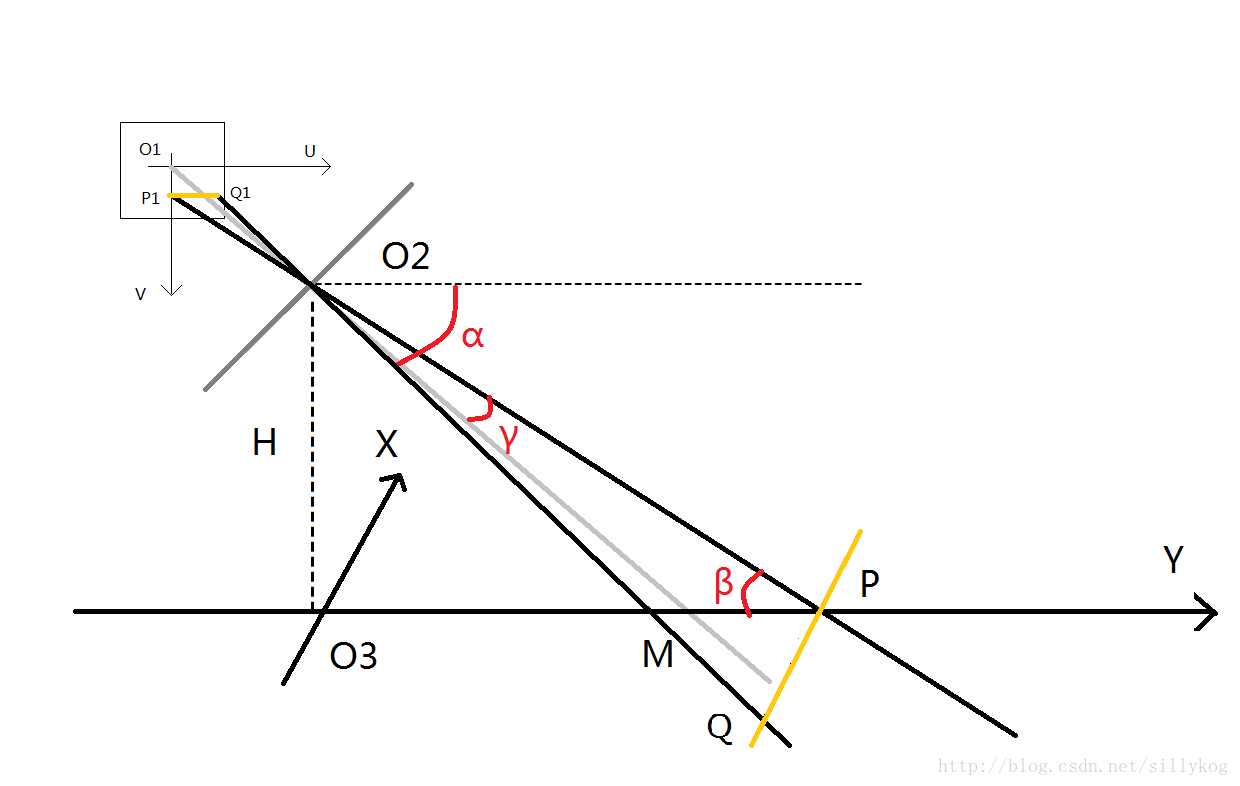
一步步推导如下：
已知量：

• 摄像机高度H
• 图像坐标中心对应的世界坐标点与摄像头在y轴上的距离$O_3M$
• 镜头中心点的图像坐标$O_1(ucenter，vcenter)$
• 测量像素点的图像坐标$P_1(u,0)、Q_1(u,v)$　　　　　
• 实际像素的长度$xpix$
• 实际像素的宽度$ypix$
• 摄像头焦距$f$

y轴方向计算和上一个模型相同，x轴计算是y轴坐标通过比例计算得到

$${ \alpha = \arctan \left( \frac { H } {O_3M} \right) } \\ { \gamma = \arctan \left( \frac { O _ { 1 } P _ { 1 } \times y p i x } { f } \right) = \frac { ( v - v c e n t e r ) * y p i x } { f } } \\ { \beta = \alpha - \gamma } \\ { O _ { 3 } P = \frac { H } { \tan ( \beta ) } }$$

这样就可以得到垂直方向的坐标：$Y=O_3P$

$${ O _ { 2 } P _ { 1 } = \sqrt { ( v - v c e n t e r ) * x p i x ) ^ { 2 } + f ^ { 2 } } } \\ { O _ { 2 } P = \frac { H } { \sin ( \beta ) } }$$

由$\frac { P Q } { P _ { 1 } Q _ { 1 } } = \frac { O _ { 2 } P } { O _ { 2 } P _ { 1 } }$得出$P Q = \frac { O _ { 2 } P \times P _ { 1 } Q _ { 1 } } {O_2P_1}$

这样就可以得到垂直方向的坐标：$X=PQ$

模型三：假设测量的点有X轴、Y轴分量，且物体有高度h　　　　

针对以下模型图我们将进行说明：

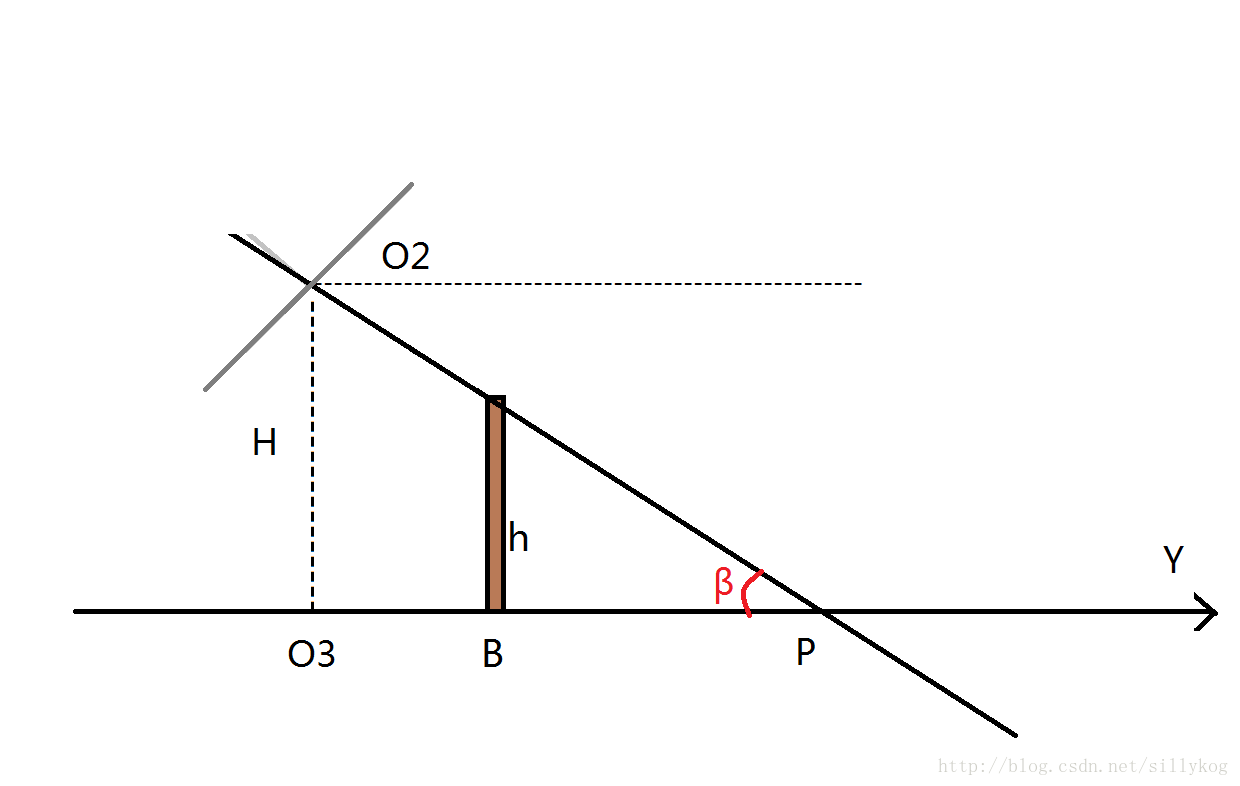
由于物体有高度，因此还需要进行一个投影变换，其实也还是相似变换　
　　
设真实的坐标$(X′,Y′)$，模型二求出的坐标$(X,Y)$，则

$$(X′,Y′)=(X,Y)×(1−\frac{h}{H})$$

　　

模型评价　　　　

实际操作过程中，发现该模型在畸变较小的图像中误差较小，且在矫正畸变后的图像中测量的图像坐标可以得到更准确的值。另一方面，在实际操作过程中，发现由于镜头有稍微歪曲或者内置感光区域安装歪了，可能导致我们找不到真正的X,Y轴，所以在测量验证的时候会有稍许误差，但即便如此，在10米的定位下，误差也不到5%，效果还是可以接受的。如果有人知道如何找到真正的X,Y轴，请博客留言告知一下，先谢谢了。

matlab计算代码下载

%%相机参数
H=217.0  % 摄像机高度H 
dis=490.0  % 图像坐标中心对应的世界坐标点与摄像头在y轴上的距离O_3M 
h=0      % 物体的高度

v=748.0   % 测量像素点的图像坐标P_1(u，0）、Q_1(u，v)　　
u=648.0
vcenter=707.606 % 镜头中心点的图像坐标O_1(ucenter，vcenter) 
ucenter=604.677 
f=1.25649   % 焦距
xpix=0.0008314 % 实际像素的长度xpix 
ypix=0.00083 % 实际像素的长度ypix 

%% Y calculation
Alpha=atan(H/dis)
y=(v-vcenter)*ypix 
Gama=atan(y/f) 
Beta=Alpha-Gama   % 原版代码这里为 + ，应该错了
Y=H/tan(Beta) 
%% Scale for depth
Yreal=Y*(1-h/H)

%% X calculation
OP=H/sin(Beta) 
tuple_sqrt(f*f+y*y,Op) % 即Op=sqrt(f*f+y*y)
x=(u-ucenter)*xpix
X=x*OP/Op 
%% Scale for depth
Xreal=X*(1-h/H)

参考

单目视觉定位测距的两种方式