极化SAR数据简介

概述

极化SAR（PolSAR）系统是在单通道SAR系统的基础上发展得到的，它能提供目标多维的遥感信息。与传统的单通道SAR相比，PolSAR不仅利用了目标散射回波的幅度、相位和频率特性，还利用了其极化特性。波长较长的L波段信息能够穿透森林和地表植被覆盖，在军事上能够用于发现丛林中或者浅埋地表的隐藏目标信息。

极化合成孔径雷达通过发射和接收不同极化方式的电磁波测量地物目标的极化散射特性，获得目标极化散射矩阵。由于电磁波的极化对目标的表面粗糙度、介电常数、几何形状和取向等物理特性比较敏感，因而极化散射矩阵蕴含着丰富的目标信息。

极化波的表征

极化的概念

首先，什么是电磁波呢？

科学家对电和磁这两种神秘力量研究了上百年，最终英国的麦克斯韦提出：电流能在其周边产生电场，变化的电场产生磁场，变化的磁场又产生电场。最终这个理论被赫兹的实验所证实。

电磁场在这样的周期性变换中，电磁波就辐射出来，向空间传播。详情见文章：“电磁波看不见摸不着，这个年轻人的奇思妙想改变了世界”。

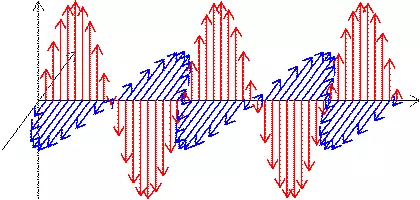
如上图所示，红色的线表示电场，蓝色的线表示磁场，电磁波的传播方向同时垂直于电场和磁场的方向。

其次，什么是极化？

极化是矢量波共有的性质，它用来描述空间某一固定点所观测到的矢量波随时间变化的特性。由于电场和磁场可根据方程互推，不失一般性，一般采用电场定义电磁波的极化。

具体而言，电磁波的极化指的是，均匀平面波（等相位面为平面，且在等相位面上同一时刻电磁场的大小和方向处处相同的电磁波）传播过程中，在某一个波阵面（在电磁波传播过程中，对应每一时刻，空间电磁场中具有相同相位的点构成的曲面）上，电场强度矢量$E$的振动状态（大小和方向）随时间变化的方式。均匀平面波是横电波，场量在传播方向上没有分量。在垂直于传播方向的平面上，可将电场矢量分解为两个互相垂直的场分量，极化描述的就是这两个分量的大小和方向的关系。更直观地说，极化描述了空间电磁波电场矢量在传播截面随时间的运动轨迹。可见，极化是电磁波的固有属性。

下图以电磁波的极化表征为例，说明各种表征方法的相互关系[2]。

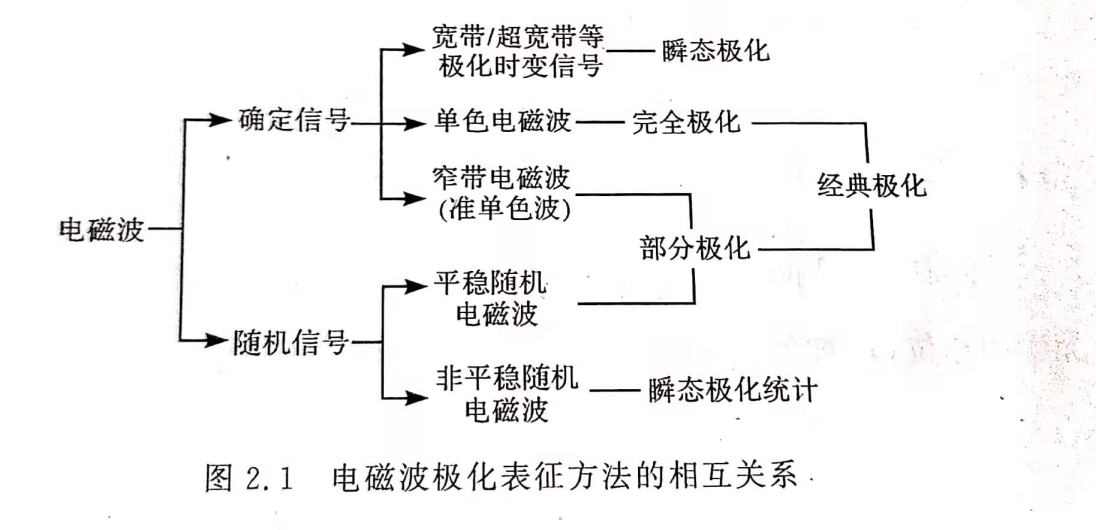
简单来说，广义的极化波分为三类[3]：

1. 完全极化波（completely polarized wave），即单色波且无噪声分量，完全极化的单色波的波参数频率$\omega$、相位$ \delta$都是常数。雷达的发射波一般可以看成完全极化波（实际上是准单色的）。

   此时电场矢端的运动轨迹为：电场矢量的端点在一个极化椭圆上随时间做周期性运动，其两个正交分量的振幅为常数，且相位差恒定的电磁波。

2. 部分极化波（partially polarized wave），它包含随机量、时变量或噪声分量。从许多自然界和人工建筑物等反射的信号都包含了很宽的频谱范围，波参数频率$\omega$、相位$ \delta$可能是时间和空间位置的函数，场矢量的幅度和相位是随机过程。此时电场矢量$E(r,t)$在空间任意点$r$、一个周期内随时间变化而形成的轨迹不再是一个不变的椭圆，而是随时间变化而变化。这种波被称为部分极化波，雷达接收的回波一般可认为是部分极化波。

   此时电场矢端的运动轨迹为：电场矢量的端点在垂直于传播方向的平面内的运动轨迹是一条形状和方向都随时间变化的类似椭圆的曲线的电磁波。

3. 非极化波（unpolarized wave），表示电场矢量分量之间完全不相关的电磁波。

   此时电场矢端的运动轨迹为：电场矢量的端点运动完全无规则的电磁波。

下图是三种波的示意图。

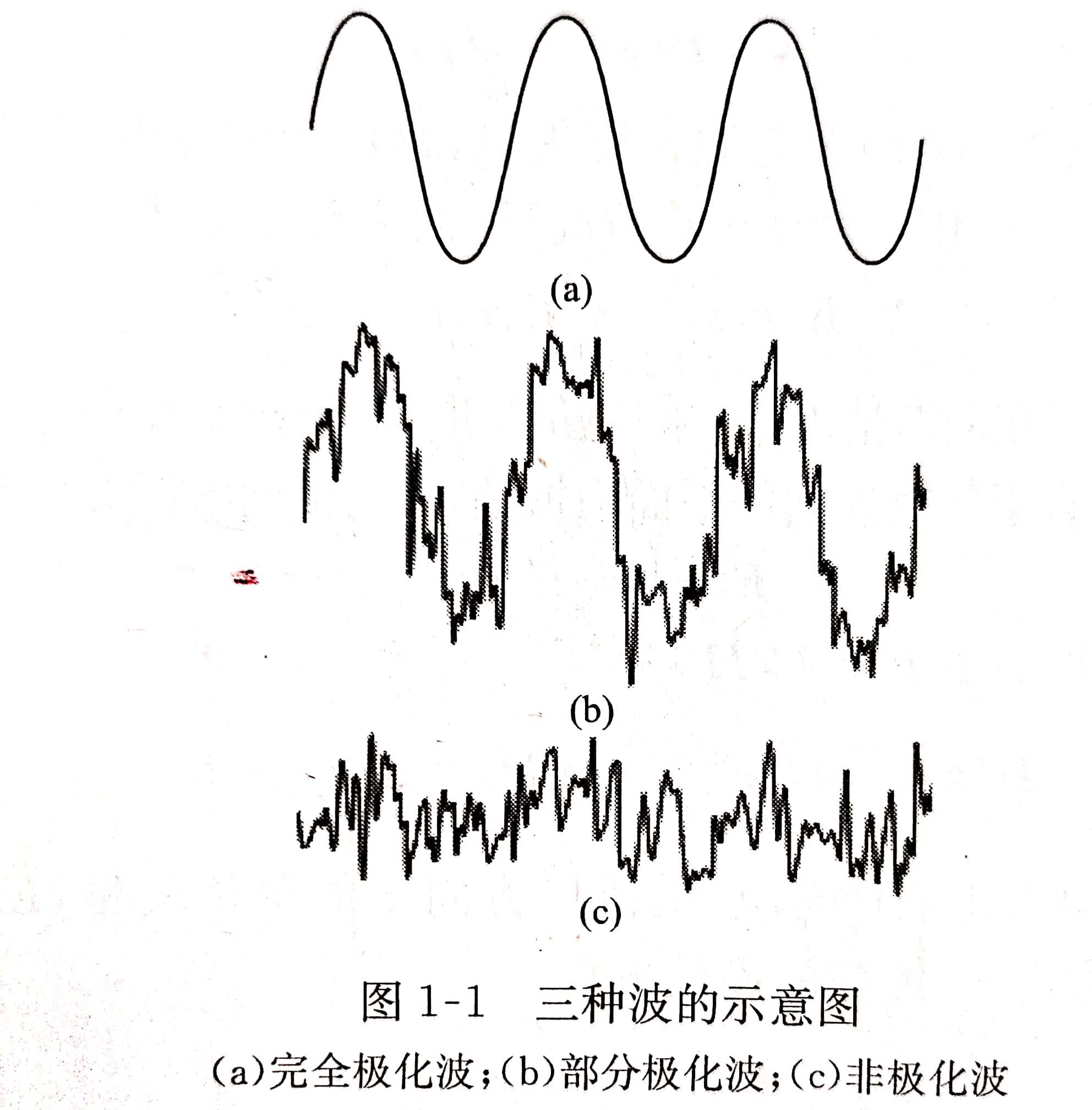
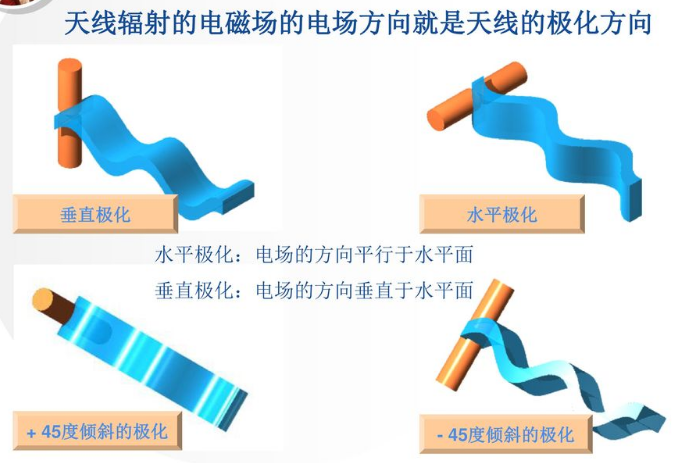
特别的，如果电场矢量端点随时间变化的轨迹是一直线，这种波称作线极化波，线极化波又分为水平极化（H）和垂直极化（V）。如果电场方向垂直于地面，我们称它为垂直极化波（V）。同理，电场方向平行于地面，就是水平极化波（H）。如果电场的方向和地面成45°夹角，我们就其称为±45°极化。如下图所示，橙色的柱子表示电场方向：

Jones与Stokes矢量表示法

电磁波可以由Jones矢量或者Stokes矢量表示。我目前还用不到这些知识，所以就先不总结了。只需要知道下面几个结论就行了：

1. Jones矢量只能用于表述完全极化波，而Stokes矢量用于表示部分极化波。
2. 下面要介绍的极化散射矩阵给出了入射波的Jones矢量和散射波的Jones矢量之间的关系，对于一个确定性的目标，当以完全极化的单色平面波照射时，其电磁散射特性可以由一个极化散射矩阵进行完全的表征。但是对于部分极化过程，需要借助Stokes矢量，得到Stokes矩阵（又称Kennaugh矩阵、Mueller矩阵）来表征。

PolSAR雷达的极化层次

按照获取极化散射矩阵的极化层次不同，极化合成孔径雷达可以分为单极化、双极化、全极化和简缩极化，表1给出极化合成孔径雷达的极化层次对比。注意下表中输出HH含义为：第一个H代表接收采用的极化方式，第二个H代表发射采用的极化方式。

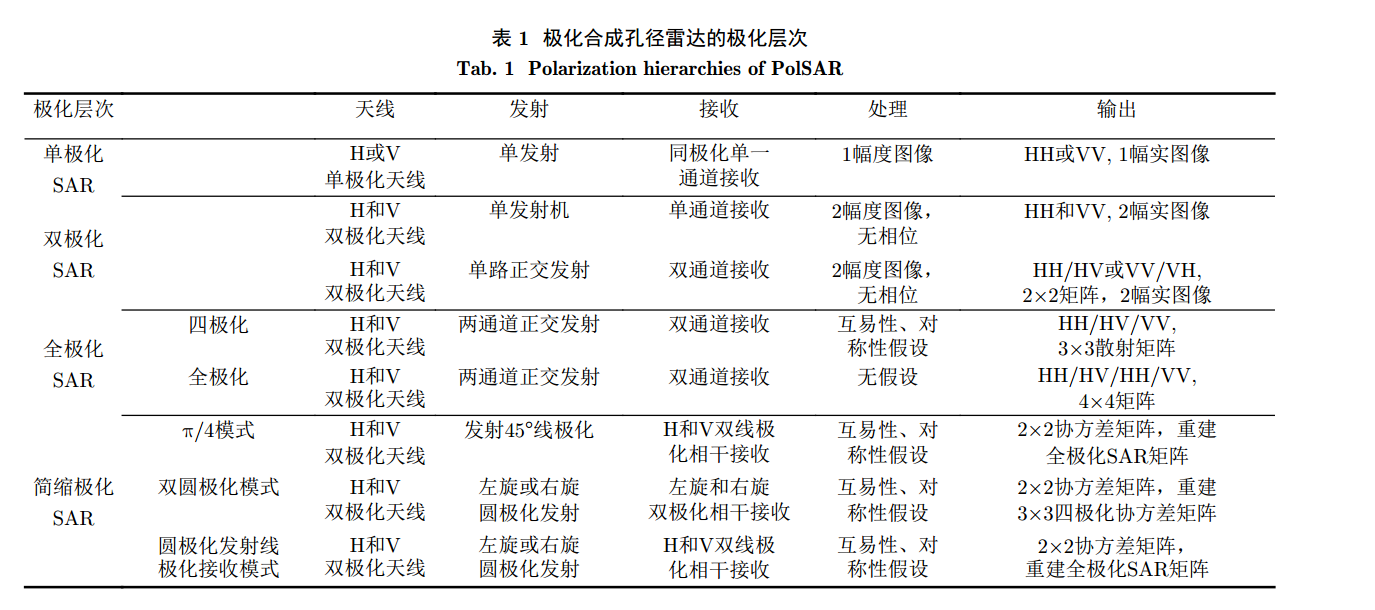
下面根据上表对极化合成孔径雷达的极化层次进行详细说明。不过值得注意的是，好多参考文献以及书籍均将上表中双极化中单路正交发射、双通道接收划分到全极化SAR类。

1. 单极化合成孔径雷达是成像雷达最基本的形式。具有单一极化天线，单一发射通道和相同极化的单一接收通道，产生HH或VV单幅实图像。

2. 双极化合成孔径雷达具有水平(H)和垂直(V)双极化天线，单路H或V极化正交发射。如果单路接收，可以得到HH和VV的两幅实图像，典型的双极化系统例子为Envisat-ASAR；如果双通道接收，可以得到HH/HV或VV/VH的2×2矩阵的两幅实图像， SIR-C、 RadarSat-2、 ALOSPALSAR都具有双极化条带模式。

3. 全极化合成孔径雷达为标准的极化合成孔径雷达，它由H和V双极化天线正交发射、双通道接收组成。发射极化与接收极化必须是正交的极化对。全极化SAR固有的数据产品是场景每一分辨单元4×4散射矩阵。如果满足互易性、对称性假设，可能产生3×3矩阵，如被压缩的Stokes矩阵，或被压缩的Sinclair散射矩阵，这种形式通常被称为四极化(Quad-Polarization)合成孔径雷达。

4. 至于简缩极化SAR，因为我不是专门研究这个的，实际我也不会用到。想详细了解的，可以看下面的参考文献。

与单极化数据相比，全极化SAR（例如上表中双极化中单路正交发射、双通道接收）在对地观测和遥感应用方面具有显著的优势。PolSAR以Stokes矩阵（或散射矩阵）形式，记录了地物任意一种极化状态下的散射回波，既有振幅信息，也有相位信息，比常规单极化或多极化雷达包含更多的地物信息，将明显提高定量雷达遥感解决应用问题的能力。例如下面要介绍的全极化SAR的极化散射矩阵表征形式中HH 数据对一些平面目标的特性表征比较好，例如可以实现土壤湿度评估、船舶的检测和水冰边界的区分； VV 数据则可以描述结构复杂的目标，例如农作物和植被、建筑物和海浪等；交叉极化方式中的 HV 和 VH 数据适合表示非均匀分布的目标特性，例如目标分布的边界、混杂分布目标场景和粗糙表面等。

散射体的极化描述

极化散射矩阵

雷达目标的电磁散射是一个线性过程，选定了散射空间坐标系以及对应的极化基，那么雷达照射波和目标散射波的各极化分量之间就存在线性变换关系，因此目标的变极化效应可以用一个复二维矩阵的形式来表示，称为极化散射矩阵。

极化散射矩阵由 Sinclair 提出，也叫做 Sinclair 矩阵，是根据电磁波不同的发射与接收组合得到一个$2 \times 2$的复数矩阵。该矩阵将目标地物的相位、 能量及极化特征统一起来，相对完整地描述了雷达目标的电磁散射特性。目标的极化特性与其形状结构有着本质的联系，可反映目标表面粗糙度、对称性和取向等其他雷达参数不能提供的信息，是完整刻画目标特性不可或缺的。

当雷达发射一组电磁波作为入射波，根据任何单色波的电磁矢量均可分解为两个相互正交的 Jones 矢量的线性组合，所以可以将入射波记为$E^{tr}=E_H^{tr}e_H + E_V^{tr}e_V$，当该电磁波遇到散射体时会根据目标散射体的散射特性产生一定的散射效应，在远场情况下散射波可视为面波，整个散射过程可看成一个线性转换过程，用矩阵$S$表示，则可用下式表达回波与入射波之间的关系：

$$\begin{eqnarray} E^{r e}=S E^{tr}=\left[\begin{array}{c}{E_{H}^{r e}} \\ {E_{V}^{r e}}\end{array}\right]=\frac{e^{i k_0 r} }{r}\left[\begin{array}{cc}{S_{H H}} & {S_{H V}} \\ {S_{V H}} & {S_{V V}}\end{array}\right]\left[\begin{array}{c}{E_{H}^{tr}} \\ {E_{V}^{tr}}\end{array}\right] \end{eqnarray}$$ $$\mathbf{S}=\left[\begin{array}{cc}{S_{H H}} & {S_{H V}} \\ {S_{V H}} & {S_{V V}}\end{array}\right]$$ $${S_{i j}=\left|S_{i j}\right| \frac{e^{i k_{0} r}}{r}, i, j \in\{H, V\}}$$

其中，$r$表示待测物体与极化SAR系统的距离，$tr$表示极化SAR系统所发射的入射波， $re $为散射波，$ k_0$ 为极化SAR 系统发射的电磁波的系数。$S$矩阵是一个复的$2\times 2$的矩阵，它包含了散射体的信息，称为极化散射矩阵。$S$中的元素$s_{x,y}$表示发射极化方式为$y$，接收极化方式为$x$时的复散射系数。又称 $S_{HH}$和$S_{VV}$为共极化分量， $S_{HV}$ 和$S_{VH}$为交叉极化分量。从式子中可以看出，对于不同的目标，$\frac{e^{i k_0 r} }{r}$是定值，所以散射波和入射波的关系可以由极化散射矩阵唯一确定。

一般情况下，极化散射矩阵具有复数的形式，它不但与目标本身的材质、形状、尺寸、结构等物理因素有关，同时也与目标和收发测量系统之间的相对姿态取向、空间几何位置关系、以及雷达工作频率等条件有关。根据单基系统以及天线互易定理，交叉极化分量是相等的，即$S_{HV}=S_{VH}=S_x$。因此$S$可表示为：

$$S=e^{i\Phi_0} \left[\begin{array}{cc}{|S_{H H}|} & {|S_{x}|e^{i(\Phi_x-\Phi_0)}} \\ {|S_{x}|e^{i(\Phi_x-\Phi_0)}} & {|S_{V V}|}e^{i(\Phi_{vv}-\Phi_0)}\end{array}\right]$$

如果忽略绝对相位值，则$S$矩阵产生5个独立参数（3个振幅量和2个相位量）。

极化合成孔径雷达对地物的探测是通过雷达对地物发射固定频率的电磁波，地物的表面因感应电流而进行辐射，从而产生散射的回波信号，依据测量地面每个分辨单元内的散射回波， 从而实现对目标特性的获取。如下图所示，给出了PolSAR测量系统的组成框图，该系统通过分时发送水平极化波和垂直极化波两种脉冲信号，并且同时接收这两种极化方式的电磁波来实现极化散射矩阵的各个元素的测量。在发射时刻，只发送一种极化方式的电磁波，极化方式由图中的发射极化开关来控制；在接收时刻，同时用水平极化天线和垂直极化天线进行接收。

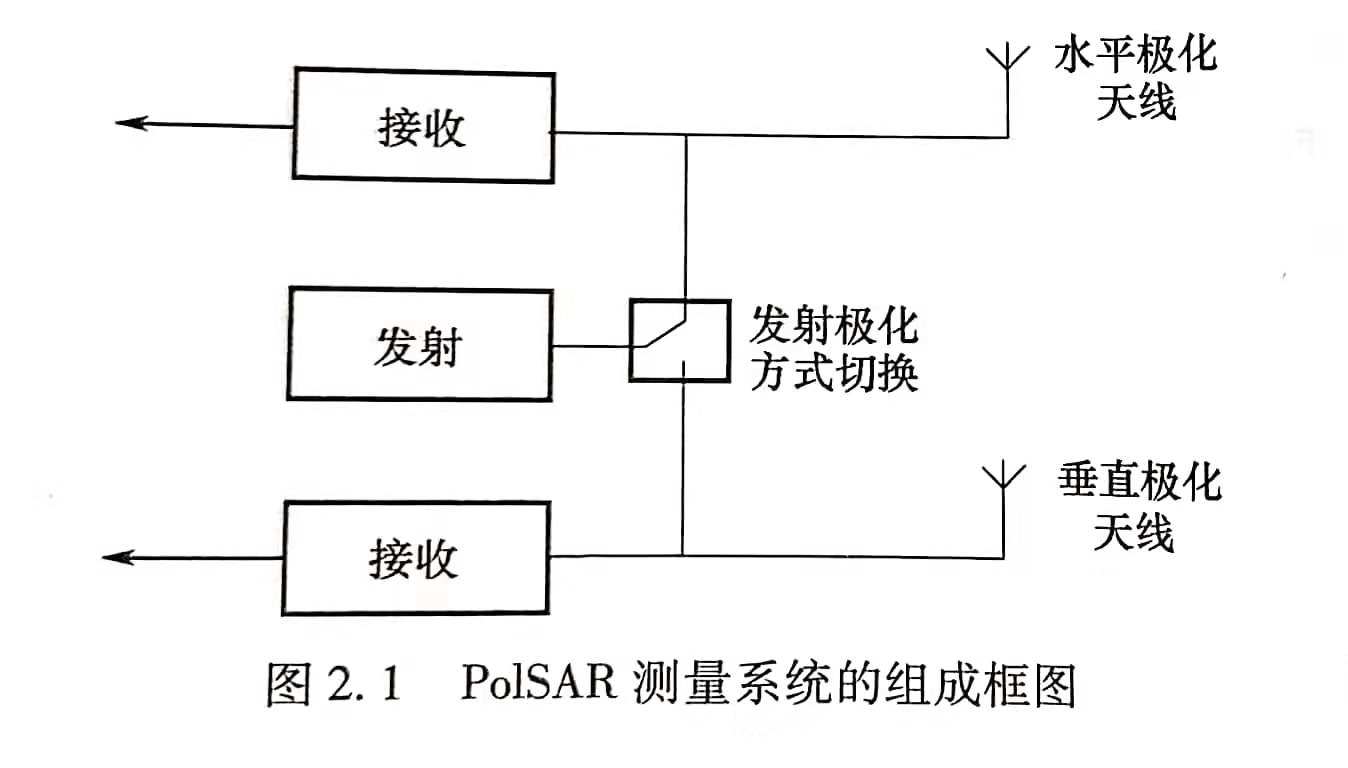
下图给出了极化散射矩阵的测量时序图。PolSAR系统首先发射某一种极化方式的电磁波，在同一时刻接收到一对正交极化回波；随后发射另外一种极化方式的电磁波，同样的同时接收到一组正交极化回波。通过上面的PolSAR系统得到的其实是4幅图像，分别为水平极化接收/水平极化发射（HH）、水平极化接收/垂直极化发射（HV）、垂直极化接收/水平极化发射（VH）、垂直极化接收/垂直极化发射（VV）。因此PolSAR图像中的每个像素的测量结果可以用一个$2\times 2$的复散射矩阵$S$来表示，极化散射矩阵$S$也称为辛克莱矩阵。

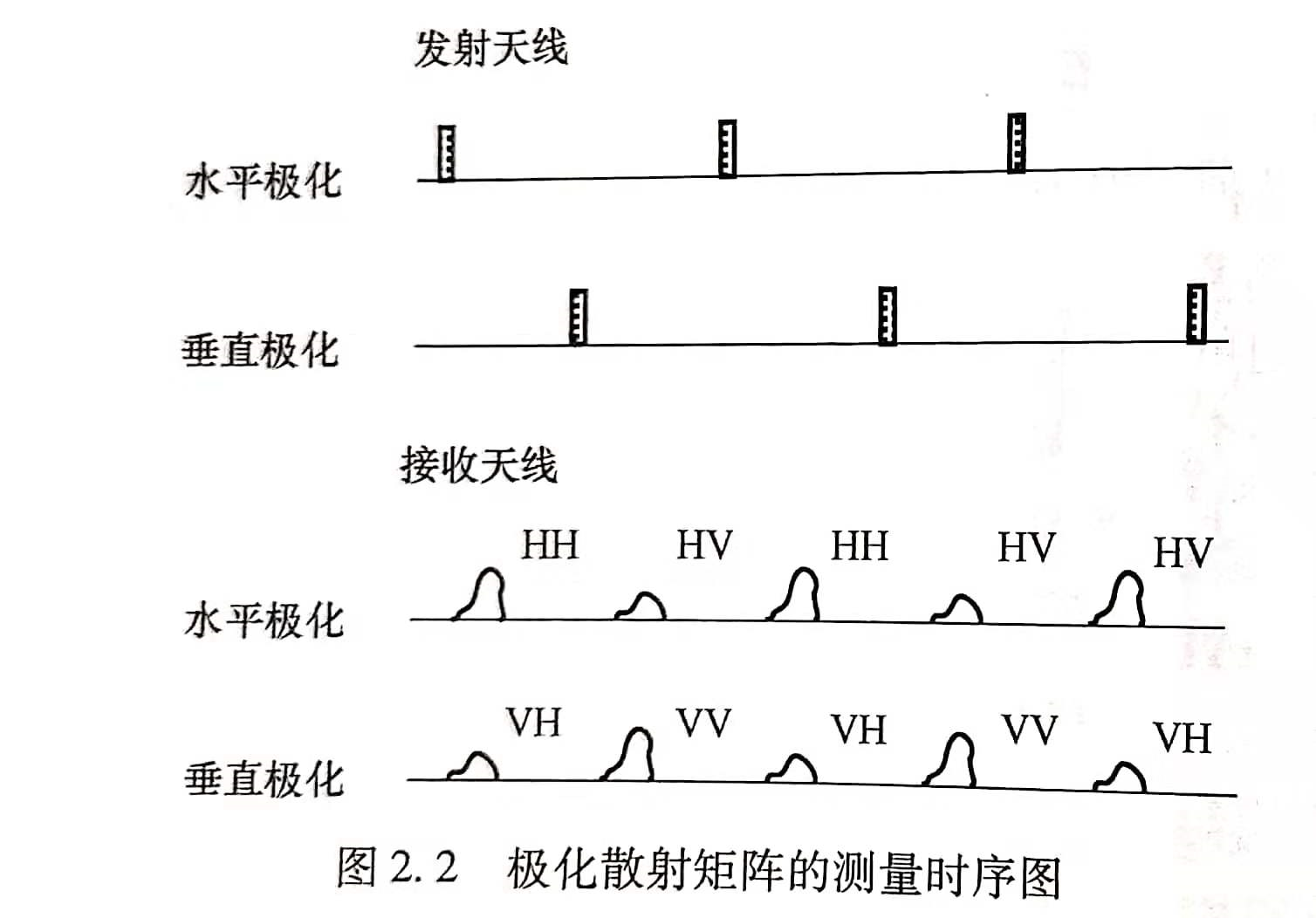
极化散射矩阵是极化SAR图像数据最基本的数据描述形式， 通过对极化散射矩阵的变换，我们可以得到其他常见的极化SAR图像数据描述形式，如 Muller 矩阵， 极化相干矩阵与极化协方差矩阵。

Stokes矩阵

前面已经说过，极化散射矩阵是由Jones矢量推导出来的，而使用Jones矢量只能表示完全极化波，所以散射矩阵描述的是一种完全极化过程，不能用于描述部分极化过程，因此，由多个地面小散射体组合形成的平均散射矩阵不能充分解释该地面的散射特性。而跟Jones矢量不同的是，Stokes矢量可以用来表示部分极化波，借助于Stokes矢量，可以得到另外一种描述散射体的方法，就是Stokes矩阵。Stokes矩阵又称Kennaugh矩阵，在前向散射坐标系中又称Mueller矩阵，反映了入射波与散射回波的Stokes矢量之间的相互关系。它是一个$4 \times 4$实矩阵，用于描述入射波和散射波的Stokes矢量之间的关系。因为我所做的数据集均是全极化数据，所以对于这种表示方式就不再赘述了。

极化散射矩阵的矢量化

极化数据的分析过程中，为了能提取出足够多的物理信息，常常需要将目标的极化散射矩阵矢量化，得到散射矢量，并迸一步得到目标的极化协方差矩阵和极化散射相关矩阵。极化协方差矩阵和极化散射相关矩阵中包含了雷达测量得到的全部极化信息，是我们进行极化数据分析和处理的基础。因此我们需要首先分析下如何对极化散射矩阵$S$进行矢量化。

散射矩阵的矢量表示，即将散射矩阵$S$用等效的四维复散射矢量$k_4$表示，定义如下：

$$\mathbf{S}=\left[\begin{array}{cc}{S_{H H}} & {S_{H V}} \\ {S_{V H}} & {S_{V V}}\end{array}\right] \Rightarrow k_4 = V(S) = \frac{1}{2}Trace(S\Psi)=\left[k_0,k_1,k_2,k_3\right]^T$$

其中，$V(\cdot)$为矢量化算子，$Trace(\cdot)$为矩阵的迹，$\Psi$为$2\times 2$的复单位矩阵，$T$为矩阵转置运算。$S\Psi$为矩阵相乘。

为了矢量化矩阵$S$，可以采用不同的正交单位矩阵。主要是两种正交单位矩阵：Lexicographic基和Pauli基。

Lexicographic基

Lexicographic基是由$S$的直接展开推导出来的。此时$\Psi_L$的形式如下：

$$\begin{eqnarray} \Psi_L = \left\{ \left[\begin{array}{c} 2 & 0 \\ 0 & 0\end{array} \right],\left[\begin{array}{c} 0 & 0 \\ 2 & 0\end{array} \right],\left[\begin{array}{c} 0 & 2 \\ 0 & 0\end{array} \right],\left[\begin{array}{c} 0 & 0 \\ 0 & 2\end{array} \right] \right\} \end{eqnarray}$$

带入上面矢量化公式，可以得到

$$k_{4L} = \left[S_{HH},S_{HV},S_{VH},S_{VV}\right]^T$$

如果PolSAR成像系统工作在单站雷达成像下，满足互易定理（即收发天线位置互换时，后向散射测量值不变）。根据互易性原理有$S_{HV}=S_{VH}$，此时散射矢量中的元素减少为3个。

$$\begin{eqnarray} k_{4L} = \left[ S_{HH},\sqrt 2 S_{HV},S_{VV} \right]^T \end{eqnarray}$$

实际中散射系数$S_{HV}$和$S_{VH}$是由不同的接收机在不同的时刻测量获得的，因此不同系统中热噪声的差异将导致两者的测量结果并不一致。在满足互易性的条件下，我们可以将$S_{HV}$和$S_{VH}$进行平均，从而减小交叉极化通道图像的噪声以提高其信噪比。进行该操作后，极化散射矢量$k_{4L}$变为

$$\begin{eqnarray} k_{4L} = \left[ S_{HH},\frac{1}{\sqrt 2} (S_{HV} + S_{VH}),S_{VV} \right]^T \end{eqnarray}$$

经过互易定理后得到的矢量化式子之所以有系数$\sqrt 2$或者$\frac{1}{\sqrt 2}$是为了保持总能量不变，即总能量始终为

$$P_{tot} = |S_{HH}|^2 + |S_{HV}|^2 + |S_{VH}|^2 + |S_{VV}|^2$$

Pauli基

当$\Psi_P$采用Pauli基，如下形式：

$$\begin{eqnarray} \Psi_P = \left\{\sqrt 2\left[\begin{array}{c} 1 & 0 \\ 0 & 1\end{array} \right],\sqrt 2\left[\begin{array}{c} 1 & 0 \\ 0 & -1\end{array} \right],\sqrt 2\left[\begin{array}{c} 0 & 1 \\ 1 & 0\end{array} \right],\sqrt 2\left[\begin{array}{c} 0 & -i \\ i & 0\end{array} \right]\right\} \end{eqnarray}$$

带入上面的矢量化公式，可得到散射矢量的另一种形式：

$$\begin{eqnarray} k_{4P} = \frac{1}{\sqrt 2}\left[S_{HH}+S_{VV},S_{HH}-S_{VV}, S_{HV}+S_{VH},i(S_{HV}-S_{VH}) \right]^T \end{eqnarray}$$

根据互易性原理有$S_{HV}=S_{VH}$，因此$k_{4P}$可以转换为：

$$\begin{eqnarray} k_{4P} = \frac{1}{\sqrt 2}\left[S_{HH}+S_{VV},S_{HH}-S_{VV},2S_{HV}\right]^T \end{eqnarray}$$

采用Pauli单位矩阵的好处在于，所得到的散射矢量的元素与波散射的物理特性非常接近，从而能够更好的解释物理散射机制。具体而言，Pauli基对应的散射矢量各元素分别对应表面散射、二面角散射和体散射，因此便于进行散射机理的分析，在实际使用中比Lexicographic基矢量的应用更加广泛。

极化相干矩阵和极化协方差矩阵

极化散射矩阵给出了入射波的Jones矢量和散射波的Jones矢量之间的关系，对于一个确定性的目标，当以完全极化的单色平面波照射时，其电磁散射特性可以由一个极化散射矩阵进行完全的表征，这种确定性目标对单色波的散射在雷达领域称为相干散射。但在实际的雷达测量中，对于复杂的目标（如目标的散射特性是时变的或者目标本身由多个独立的子散射体所构成，也称为分布式目标），雷达回波是时变的或者不相干的，目标的散射特性表现出一定的随机性，因此必须采用统计的方法研究目标的电磁散射特性；同时，由于全极化SAR是相干系统，散射矩阵$S$的各分量受到相干斑噪声影响较大，为了抑制噪声对观测信息的干扰，也需要采用统计方法对观测数据进行多视处理。为了能釆用统计方法进行分析，必须使用二阶统计量。常用的二阶统计量有极化协方差矩阵$C$和极化相干矩阵$T$，它们的计算基于极化散射矩阵矢量化，定义分别为

$$\begin{eqnarray} C = \left<k_{4L} \cdot k_{4L}^H \right> \end{eqnarray}$$ $$\begin{eqnarray} T = \left<k_{4P} \cdot k_{4P}^H \right> \end{eqnarray}$$

其中，$H$表示复共轭。$\left< \cdot \right>$为空间统计平均运算符。

由$k_{4L}$的表达式可以得到极化协方差矩阵$C$可以表示为下式：

$$\begin{eqnarray} C = \left<k_{4L} \cdot k_{4L}^H \right> = \left[\begin{array}{ccc} {\left\langle\left|S_{H H}\right|^{2}\right\rangle} & {\sqrt{2}\left\langle S_{H H} S_{H V}^{*}\right\rangle} & {\left\langle S_{H H} S_{V V}^{*}\right\rangle} \\ {\sqrt{2}\left\langle S_{H V} S_{H H}^{*}\right\rangle} & { 2\left\langle\left| S_{H V}\right|^2 \right\rangle} & {\sqrt{2}\left\langle S_{H V} S_{V V}^{*}\right\rangle} \\ {\left\langle S_{V V} S_{H H}^{*}\right\rangle} & {\sqrt{2}\left\langle S_{V V} S_{H V}^{*}\right\rangle} & {\left\langle\left| S_{V V}\right|^2 \right\rangle} \end{array}\right] \end{eqnarray}$$

由$k_{4P}$的表达式可以得到极化相干矩阵$T$可以表示为下式：

$$\begin{eqnarray} \begin{split} T &=& \left<k_{4P} \cdot k_{4P}^H \right> \\&=& \frac{1}{2}\left[\begin{array}{ccc} {\left\langle\left|S_{H H}+S_{V V}\right|^{2}\right\rangle} & {\left\langle\left(S_{H H}+S_{V V}\right)\left(S_{H H}-S_{V V}\right)^{*}\right\rangle} & { 2\left\langle\left(S_{H H}+S_{V V}\right) S_{H V}^{*}\right\rangle} \\ {\left\langle\left(S_{H H}-S_{V V}\right)\left(S_{H H}+S_{V V}\right)^{*}\right\rangle} & {\left\langle\left|S_{H H}-S_{V V}\right|^{2}\right\rangle} & { 2\left\langle\left(S_{H H}-S_{V V}\right) S_{H V}^{*}\right\rangle} \\ { 2\left\langle S_{H V}\left(S_{H H}+S_{V V}\right)^{*}\right\rangle} & { 2\left\langle S_{H V}\left(S_{H H}-S_{V V}\right)^{*}\right\rangle} & { 4\left\langle\left. S_{H V}\right|^2 \right\rangle} \end{array}\right] \end{split} \end{eqnarray}$$

极化协方差矩阵$C$和极化相干矩阵$T$均是半正定的Hermitian矩阵，两者可以互相转换：

$$\begin{eqnarray} C = U^HTU=U^{-1}TU \end{eqnarray}$$ $$\begin{eqnarray} T=UCU^H=UCU^{-1} \end{eqnarray}$$

其中，$U$为单位转换矩阵，其形式为：

$$\begin{eqnarray} U=\frac{1}{\sqrt 2}\left[ \begin{array}{c}1 & 0 & 1 \\ 1 & 0 & -1 \\ 0 & \sqrt 2 & 0\end{array}\right] \end{eqnarray}$$

并且满足，$|U|=1$，$U^{-1}=U^H$。

极化SAR目标分解

从极化SAR图像数据中，我们可以提取目标的极化散射特性，从而实现全极化数据的分类、检测和识别等其它应用。这我们需要对极化数据进行分析，有效地提取出目标的散射特性，其理论核心是目标极化分解。目标分解理论是为了更好地解译极化数据而发展起来的。目标分解定理最早由Huynen提出，它有助于利用极化散射矩阵揭示散射体的物理机理，促进对极化信息的充分利用，收到了雷达工作者的重视。

经过近30年的发展，各种目标分解方法相继产生，根据目标散射特性的变化与否，极化目标分解的方法大致可以分为两类：一类是针对目标散射矩阵的分解，此时要求目标的散射特征是确定的或稳态的，散射回波是相干的，故也称为相干目标分解（coherent target decomposition，CTD）；另一类是针对极化协方差矩阵、极化相干矩阵、Mueller矩阵或Stokes矩阵的分解，此时目标散射可以是非确定的（或时变的），回波是非相干的（会部分相干）的，故也称为非相干矩阵分解（incoherent target decomposition，ICTD）。

相干目标分解方法包括Pauli分解、SDH分解、Cameron分解和SSCM分解。该类分解方法主要是基于极化散射矩阵[S]的分解。在应用中，通常要求目标的散射矩阵是确定不变的或者稳态的。然而，对于大自然中大量存在的复杂目标（或非确定性目标）而言，目标散射特性呈现很强的变化性，复杂目标对入射波的散射行为可以看做一个随机过程，对此类目标散射特性的描述需要采用统计的方法，一般通过多次测量或集合平均的方法，得到能表征目标极化散射特性的极化相干矩阵[T]、极化协方差矩阵[C]、Muller矩阵[M]或Stokes矩阵[K]等，由于这几类矩阵的相互转换性，实际中大多只针对极化相干矩阵[M]进行分解。这类分解包括Huynen分解，Cloude分解，Holm&Barnes分解以及Freeman-Durden分解等。

最后需要注意的是，由于在非相干目标分解之前需要进行集合平均计算，这个过程会损失一些目标信息，而相干目标分解木有经过期望平均运算，所以不会损失任何关于目标的信息。

下面我对相干极化目标分解中的Pauli分解做详细的说明。其余的分解方式因为暂时用不到，所以就不再赘述了。

散射矩阵$S$的相干分解方法的主要思想是将任意散射矩阵$S$表示成基本目标的散射矩阵之和的形式，这些基本散射矩阵可以与某种确定的散射机理联系起来：

$$S = \sum_{i=1}^k c_i S_i$$

其中$S_i$代表每个基本目标的散射矩阵，$c_i$表示$S_i$在组合中的权重。为了简化问题，假设各矩阵$S_i$具有独立性，避免一个特定的散射行为表现在多个矩阵$S_i$中。

当入射波和散射波均是完全极化波时，散射矩阵$S$才可以描述特定目标的散射过程。因此，相干目标分解只能用来研究所谓的相干目标（Coherent Target），也称为点目标或者纯目标。在实际情况中，测量的散射矩阵$S$往往对应一个复杂的相干目标。只有在极少情况下，该矩阵对应于一个更简单或者基本目标。然而，为了推断出研究目标的物理特性，直接分析$S$通常非常困难。因此，需要用更简单的散射矩阵$S_i$和相应系数$c_i$来提取和解释目标的物理特性。

Pauli分解选择Pauli基$\{S_a,S_b,S_c,S_d\}$作为它的基本散射矩阵，在正交线性基（H，V）下，Pauli基用下面的$2 \times 2$矩阵表示：

$$S_a = \frac{1}{\sqrt 2}\left[\begin{array}{c} 1 & 0 \\ 0 & 1\end{array} \right],S_b = \frac{1}{\sqrt 2}\left[\begin{array}{c} 1 & 0 \\ 0 & -1\end{array} \right],S_c = \frac{1}{\sqrt 2}\left[\begin{array}{c} 0 & 1 \\ 1 & 0\end{array} \right],S_d = \frac{1}{\sqrt 2}\left[\begin{array}{c} 0 & -i \\ i & 0\end{array} \right]$$

因此，对于要研究的散射矩阵$S$，它可以写成如下形式：

$$S = \left[\begin{array}{cc}{S_{H H}} & {S_{H V}} \\ {S_{V H}} & {S_{V V}}\end{array}\right] = a S_a + b S_b + c S_c + d S_d$$

其中，$a,b,c,d$均是复数，可以写成向量$K$的形式：

$$K=\left[a \ b \ c \ d \right]\\=\frac{1}{\sqrt 2}\left( S_{HH}+S_{VV} \ \ S_{HH}-S_{VV} \ \ S_{HV}+S_{VH} \ \ i(S_{VH}-S_{HV}) \right)^T$$

从上式中可以看出，Pauli分解具有保持总功率不变的性质，即

$$SPAN=|S_{HH}|^2+|S_{HV}|^2+|S_{VH}|^2+|S_{VV}|^2=|a|^2+|b|^2+|c|^2+|d|^2$$

Pauli分解可以看成四种散射机制的相干分解。如下表所示：

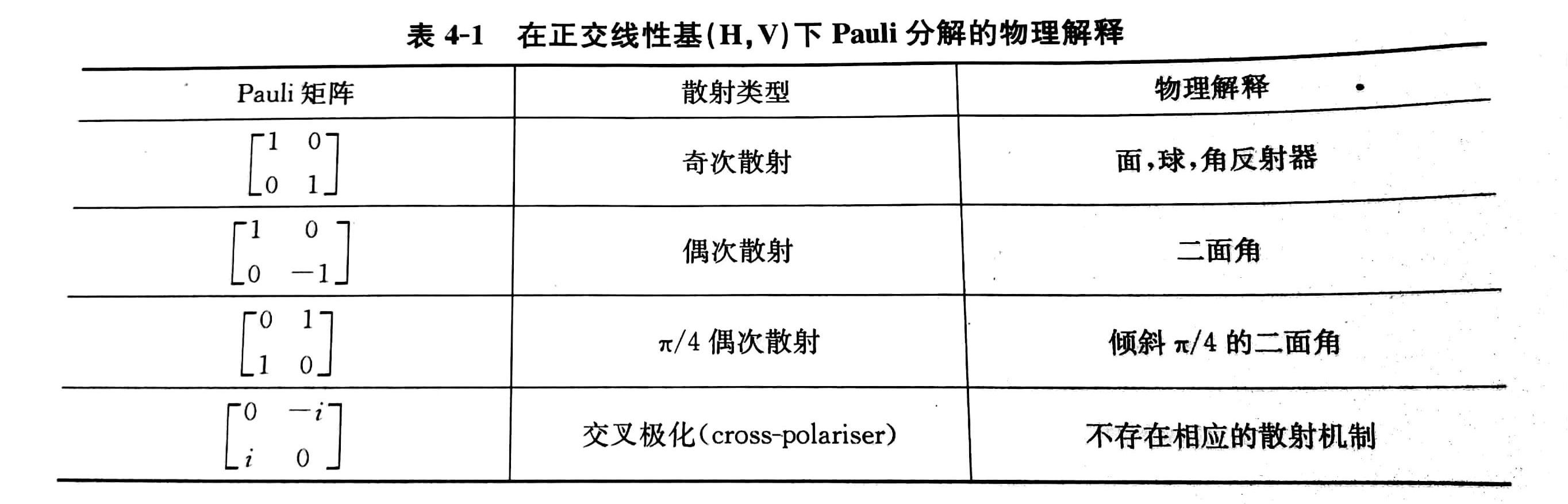
下面对这个表格进行详细说明：

1. 第一个矩阵$S_a$可以理解为单次或奇次散射机制，例如，球体、平坦表面或者三面角反射器都是这类典型的散射体。复系数$a$表示$S_a$对散射矩阵$S$最终测量的贡献。特利地，该系数的强度，即$|a|^2$决定了那此具有奇次散射特征的散射体的散射能量。

2. 第二个矩阵$S_b$表示绕轴旋转0°的二面角散射机制。由于回波极化与人射波极化关于镜面对称，因此，该分量表示具有二次或偶次反射的散射机制。$b$表示该类散射机制的复系数，而$|b|^2$表示该类目标的散射能量。

3. 第三个矩阵$S_c$表示绕轴旋转45°的二面角散射机制。从Pauli基可以观察到，在正交线性基（H,V）下，目标的回波极化与入射波极化正交，也就是说$S_c$对应的散射机制指示着那些能够反射回正交极化的散射体，所以，有时也与非相干散射描述联系起来，看成“”漫散射”或“体散射”，如由森林树冠产生的体散射。$c$表示该类散射机制的复系数，$|c|^2$表示该类目标的散射能量。

4. 第四个矩阵$S_d$表示矩阵$S$的所有反对称分量，对应着将每个入射极化转换成正交状态的散射体。 在真实自然世界里不存在相应的散射机制，而且考虑单基雷达系统的互易性，那么$S_{HV}=S_{VH}$。因此，$d=0$，也就是说，最后一种散射机制对散射矩阵$S$最终测量贡献为0。

Pauli分解的有点在于它非常简单，Pauli基是完备正交基，具有一定的抗噪性，即使是在有噪声或去极化效应的情况下，仍能用它进行分解。它的主要缺点在于只能区分两种散射机制：奇次散射和偶次散射，不能完整的描述实际情况。

散射矩阵的Pauli分解常用来在一幅SAR图像里表征散射矩阵$S$中所有的极化信息。以前常用的方法是组合强度信息$|S_{HH}|^2,|S_{VV}|^2,2|S_{HV}|^2$，该方法的主要缺点在于，虽然这种表达直接与极化系统测量相联系，然而，正如前面所叙述那样，$|a|^2,|b|^2,|c|^2$才对应着明显的物理散射机制。因此，利用Pauli分解各系数，可以合成另外一种RGB图像：

$$|a|^2 \rightarrow Blue \\ |b|^2 \rightarrow Red \\ |c|^2 \rightarrow Green$$

这样，上式对应的散射机制来解译相应的RGB图像。

公共数据

下载

你可以从这里下载Flevoland地区L波段的农田图、Foloum 地区L 波段图、L波段全极化成像方式对旧金山海湾成像的San Francisco地区子图。

读取

从上面下载下来的是一个压缩包，解压后为一个STK文件和一个PDF文件，无论是在Google还是baidu都搜不到相关信息。机智的我直接再github上搜包含FLEVOL.STK名字的代码。终于发现了新大陆。处理该类型数据集需要使用到Gdal软件，它的文档在这里可以找到，它的github地址可以在这里找到，它的Python文档在这里。

在Windows可以直接在这里下载对应你自己Python版本的Whl文件，直接使用pip指令安装即可。

Gdal支持很多格式，具体支持格式可以在这里查看，在这里可以查看Gdal对STK文件的支持。

论文常用数据集

值得注意的是，上面下载的数据集是没有gound truth的。因为我是要那极化SAR数据去做分类的，所以没有ground truth的数据集对我来说没有什么用。经过左右来回询问实验室师兄师姐和老师，要到了一些带ground truth的数据集，具体有哪些数据集，整理如下：

• 荷兰 Flevoland 地区农田数据集， 是由 NASA/JPL ARISAR 获取的荷兰 Flevoland 地区的 L 波段图像数据。这是一个大小为 750×1024 的四视全极化图像，12m×6m 分辨率(距离向×方位向)，包括 15 类不同的地物（不含背景），分别是干豆、油菜籽、裸地、土豆、甜菜、三种小麦、豌豆、苜蓿、大麦、草地、森林、水域、建筑区。无标记区在真实类标图上是白色标记。去掉背景类后，15类不同的地物总数为167712。
• 美国旧金山湾的 L 波段数据（San Franciso Bay 数据集），该数据是一个由美国 NASA 在1992年提供的 1300×1200 大小的L 波段的四视全极化 SAR 图像，共包含有海洋、植被、非密集型城市、密集城市和发达地区五类地物。
• 德国航空航天中心 DLR 的 ESAR 系统获得的完全极化图像数据，距离向 10 米的分辨率以及 5 米的方位向分辨率，大小为 1300×1200。该区域地物被分为四类即森林、建筑、开放区和道路。
• 加拿大 RADARSAT-2 获得的中国西安区域的极化 SAR 图像。 该图像数据的分辨率为 10×5m 、尺寸为512×512， 包含了城镇、植被和河流三种地物类型。
• 荷兰 Flevoland1 地区极化 SAR 图像。Flevoland1地区的极化 SAR 图像是由 RADARSAT-2 获取的荷兰 Flevoland1 地区的 C 波段图像数据，是一个大小为 1200×950 （或者1400x1200分辨率）、分辨率为 10×5m 的全极化图像。包括城镇、水域、森林和耕地四类不同的地物。
• Oberpfaffenhofen 数据集由德国宇航中心 E-SAR 传感器获取得 L 波段的全极化雷达数据集。该极化雷达图像的距离分辨率和方向分辨率分辨是 1.4 米和 0.92 米，图像大小为 1300× 1300。该区域包括五类： 郊区、农田、铁路、森林、其他。该数据集是属于全分数据集，相比其他雷达数据集分类难度有所提升，因此经常被用于检测所提出方法的有效性。
• 西安数据集1是 RADARSAT-2 卫星获得的 C 波段的单视全极化 SAR 图像数据的子图，场景取自中国西安西部京昆高速地区，图像大小是 512×512，分类难度中等，距离向分辨率和方位向分辨率为 8 米，该场景包括两类，分别是裸地、城区。
• 西安数据集2是2010 年由 RADARSAT-2 卫星获取，场景取自中国西安西部渭河地区，分辨率8m×8m。此极化 SAR 图像数据是大小为 300×300 单视全极化合成孔径雷达图像，分别包括城区、植被、河流、其他类别。

数据预处理

极化SAR数据集因为是复数数据，所以如果想用神经网络去做，肯定需要对其进行处理。具体有什么处理方式呢？我看了几篇师兄师姐的论文，总结了一下。

因为极化协方差矩阵和极化散射相关矩阵中包含了雷达测量得到的全部极化信息，所以经常使用极化协方差矩阵用来表示每一个像素值的特征。而极化协方差矩阵有如下几个特性：

• 每一个值均为复数值
• 对角线上元素为实数
• 复共轭矩阵

预处理方式一

对于只能使用实数的算法，需要将复数数据实值化，而又因为极化协方差矩阵为复共轭矩阵，因此极化SAR数据第$i$个像素点的特征向量$I_i$可以表示为：

$$\begin{eqnarray} I_i = \left( C_{11}, C_{22}, C_{33}, Re\left[C_{12}\right], Re\left[C_{13}\right], Re\left[C_{23}\right], Im\left[C_{21}\right], Im\left[C_{31}\right], Im\left[C_{32}\right]\right) \end{eqnarray}$$

其中，$Re$表示取复数的实数部分，$Im$表示取复数的虚数部分，而$C_{ij}$表示协方差矩阵的第$i$行第$j$列数据。经过观察，$I_i$中的每一个值都很小，因此需要进行标准化处理。

预处理方式二

对于只能使用实数的算法，基于空间一致性假设， 空间近邻的像素点往往有相同的类别，因此我们以待分类像素为中心点， 利用其空间邻域信息， 取其空间近邻窗口中的所有像素点信息来构建特征向量。 空间信息的利用可以有效避免噪声干扰，提高分类器的性能。像素点 $i$ 的最终输入特征向量$x_i$可以表达为：

$$\begin{eqnarray} x_i = \left[ I_{i-r-1}, I_{i-r}, I_{i-r+1}, I_{i-1}, I_{i}, I_{i+1}, I_{i+r-1}, I_{i+r}, I_{i+r+1}\right] \end{eqnarray}$$

其中，$r$表示极化SAR图像每行有多少个像素点。$I_i$和上述预处理方式一中的$I_i$表达式一致。

预处理方式三

对于支持复数处理的算法，直接使用某个像素点的极化协方差矩阵作为该像素点的特征即可。

参考

[1] Ruliang Y , Bowei D , Haiying L . Polarization Hierarchy and System Operating Architecture for Polarimetric Synthetic Aperture Radar[J]. Journal of Radars, 2016, 5(2).
[2] 极化雷达成像处理与应用. 肖顺平等
[3] 全极化合成孔径雷达图像处理. 王超等
通俗易懂！看完你就是半个天线专家了 - 蜉蝣采采的文章 - 知乎
极化SAR图像基础知识(2)
windows 环境下基于Python 的GDAL 安装
极化SAR图像基础知识(1)