Kaggle比赛经验

基本知识

反馈的分数是基于测试集的一部分计算的，剩下的另一部分会被用于计算最终的结果。所以最后排名会变动。
LB 指的就是在 Leaderboard 得到的分数，由上，有 Public LB 和 Private LB 之分。
自己做的 Cross Validation 得到的分数一般称为 CV 或是 Local CV。一般来说 CV 的结果比 LB 要可靠。

数据标准化

数据需要进行归一化或者标准化的重要性就不再提了，想必大家都知道。在Pytorch中，对于图像数据，通常使用totensor方法进行归一化，然后使用normalize方法进行标准化。另外，在使用ImageNet预训练权重的时候，均值和方差也尽量使用ImageNet数据的均值和方差。在siim-acr-pneumothorax-segmentation比赛中，数据为胸部放射图像，使用ImageNet数据的均值方差比使用该数据集的均值方差效果好。一种解释是，网络本质学习的是数据的分布，使用ImageNet的均值和方差可以保证得到的数据分布和预训练权重学习到的数据分布相差不大。当然，使用ImageNet数据的均值方差不一定一定比特定数据集的均值方差好，这需要实验。

数据增强

图像比赛的一个重头戏就是数据增强，我们为什么要做数据增强呢？

我们的训练模型是为了拟合原样本的分布，但如果训练集的样本数和多样性不能很好地代表实际分布，那就容易发生过拟合训练集的现象。数据增强使用人类先验，尽量在原样本分布中增加新的样本点，是缓解过拟合的一个重要方法。

需要小心的是，数据增强的样本点最好不要将原分布的变化范围扩大，比如训练集以及测试集的光照分布十分均匀，就不要做光照变化的数据增强，因为这样只会增加拟合新训练集的难度，对测试集的泛化性能提升却比较小。另外，新增加的样本点最好和原样本点有较大不同，不能随便换掉几个像素就说是一个新的样本，这种变化对大部分模型来说基本是可以忽略的。

一些常见的图像数据增强方式有：

亮度，饱和度，对比度的随机变化
随机裁剪（Random Crop）
随机缩放（Random Resize）
水平/垂直翻转（Horizontal/Vertiacal Filp）
旋转（Rotation）
加模糊（Blurring）
加高斯噪声（Gaussian Noise）

对于这个卫星图像识别的任务来说，最好的数据增强方法是什么呢？显然是旋转和翻转。具体来说，我们对这个数据集一张图片先进行水平翻转得到两种表示，再配合0度，90度，180度，270度的旋转，可以获得一张图的八种表示。以人类的先验来看，新的图片与原来的图片是属于同一个分布的，标签也不应该发生任何变化，而对于一个卷积神经网络来说，它又是8张不同的图片。比如下图就是某张图片的八个方向，光看这些我们都没办法判断哪张图是原图，但显然它们拥有相同的标签。

其他的数据增强方法就没那么好用了，我们挑几个分析：

亮度，饱和度，对比度随机变化：在这个比赛的数据集中，官方已经对图片进行了比较好的预处理，亮度、饱和度、对比度的波动都比较小，所以在这些属性上进行数据增强没有什么好处。
随机缩放：根据比赛在Overview和Data部分的信息。这些图片中的一个像素宽大概对应3.7米，也不应该有太大的波动，所以随机缩放不会有立竿见影的增强效果。
随机裁剪：观察Data，有些图片因为边上出现了一小片云朵，被标注了partly cloudy，如果随机裁剪有可能把这块云朵裁掉，但是label却仍然有partly cloudy，这显然是在引入错误的标注样本，有百害而无一利。同样的例子也出现在别的类别上，说明随机裁剪的方法并不适合这个任务。

一旦做了这些操作，新的图片会扩大原样本的分布，所以这些数据增强也就没有翻转、旋转那么优先。在最后的方案中，我们只用了旋转和翻转。并不是说其他数据增强完全没效果，只是相比旋转和翻转，它们带来的好处没那么直接。

模型

本来觉得，模型这部分没啥好记录的，都是因任务而异嘛。但是现在发现还是可以总结一些东西的。

尽可能的使用预训练模型，即使自己的数据分布和ImageNet的数据分布可能相差很大。但是这些数据可能有一些相似的特性，比如纹理、边缘特征等，神经网络中浅层的一些滤波器可能负责提取这部分特征。所以使用预训练权重，一来可以提高精度，二来可以加快收敛速度。详细的讨论在这个帖子
这个帖子讨论了在图像分辨率更高的情况下，使用更宽(通道，channel)的模型比使用更深的模型效果更好。

如何挑选合适学习率

学习率的影响

一维损失

如上图所示，如果学习率太慢，网络需要很多次迭代才会收敛；而如果学习率过大，会导致每一次迭代均跳过最小点，永远不会得到可接受的loss。更糟糕的是，更高的学习率会导致loss增加直到Nan。

这是为什么呢？如果梯度比较大，较高的学习率会导致loss远离最小值，设置可能比之前的loss更大。如下面简单的抛物线，看看高学习率是如何迅速让你越来越远离极小值的。

如上面所示，当loss处于$a_0$时，较高的学习率会导致loss跑到$a_1$点，此时loss反而上升了；当loss在$a_1$点时，较高的学习率会导致loss跑到$a_2$点，此时loss又进一步上升了。

多维损失

如果梯度下降法工作在多维损失，那么还会出现其它问题。其中一种情况如上面图所示。该图展示了一个二维场景，其中损失函数在一个维度上的斜率特别陡峭，而在另外一个维度上斜率很小；即它的形状为狭窄陡峭的山谷。
如果我们在这种情况下使用梯度下降，我们将得到上图中所示的行为（这是一维图中行为的二维模拟）。沿着目标函数陡峭部分的参数在山谷斜坡之间来回振荡，而沿着损失函数较浅部分的参数沿山谷缓慢移动。这样做的最终结果是收敛非常缓慢。图的右侧显示了更理想的收敛行为。
当梯度下降在多维空间中作用时，出现的另一个问题是鞍点。这些被定义为损失函数表面上的区域，当沿着一个维度观察时是一个极小值，当沿着另一个维度观察时同时是一个极大值。下图中的二维情况说明了这一点。
当迭代从上面接近鞍点时，即使它不是最小值，它的斜率也会达到零。其结果是迭代过程停止，算法陷入一个非最优点。这个bevavior在下图中进一步说明。

总结

如前所述，学习速率参数对梯度下降算法的有效性有很大的影响。如果它被设置为一个大的值，那么算法在迭代开始时快速收敛，但是大的学习率在系统接近最小值时，会导致参数超调，这可能导致振荡。如果学习率过小，则算法收敛性好，但可能需要很长时间。因此理想的学习率应设置自适应，这样在初始优化阶段较大，并且随着逐渐变得越来越小。

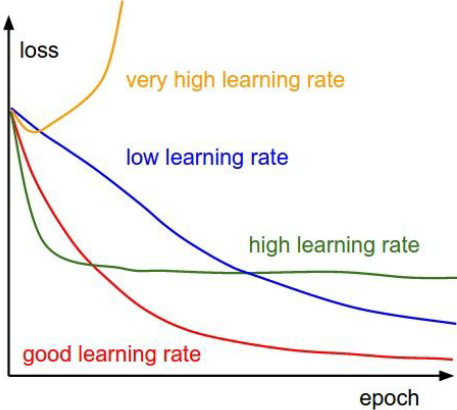
上图说明了训练过程中学习率对损失函数的影响，可用于快速检查正在使用的学习率的适用性，注意这是在训练集上的损失曲线：

一个非常高的学习率会导致损失函数在几次迭代后开始增加
一个偏高的学习率会导致损失在最初的快速下降后以一个较高的值进入平稳期
一个非常低的学习率在训练阶段导致损失函数缓慢收敛
合适的学习率结合了初始阶段的快速下降和较低的平稳值

另外，如果在验证集上的损失曲线先下降或上升，则是过拟合。造成这种现象的原因是因为模型容量与数据复杂度不匹配或者训练数据集造成的。个人觉得跟学习率大小没有过大的关联。

理论

所以我们如何挑选合适的学习率呢？在这篇文章中，提供了一个可行的方法。以SGD优化器为例，对于一个epoch，初始学习率特别低（例如$10^{-8}$），然后在每一个mini-batch均乘上一个因子改变学习率，直到它达到一个特别高的值（例如1或者10）。然后在每一次迭代均记录损失值，画出训练过程中loss关于学习率（取log后）的曲线，例如下面所示：

如上图所示，loss在一开始一直下降，然后停止下降，最后开始上升。这会因为，使用非常低的学习率时，我们的结果越来越好，特别是当我们增加学习率时。当学习率达到特别高的值时，loss开始增加。那么最好的学习率是什么呢？令你想不到的是，不是最低loss对应的学习率。

这是为什么呢？最低loss对应的学习率其实已经开始有点太高了，因为我们处于改进和退步之间的边缘。我们在这个值之前取一个值，那么这个值仍然可以用来快速训练，并且仍然是安全的，不会出现梯度爆炸。如上图所示，我们选择的是$10^{-2}$，而不是$10^{-1}$。

该方法可以应用于SGD的任何变体，也可以应用于任何类型的网络。我们只需要经历一个epoch(通常更短)，并记录我们损失值，就可以为选出合适的学习率。

实际我使用的时候，感觉并不是很适用。在画这个曲线的时候，是否应该将所有的数据增强、数据多尺度均关闭？这个问题暂时没有解决。另外，这种方法得到的学习率偏大，可以考虑设置为它的四分之一左右。

实践

在实践中，我们通常不会会出每一个mini-batch的loss曲线，而是它的平滑版本。如果非要画出每一个mini-batch的loss曲线，我们将会得到像下面这样的图：

即使我们可以看到总体趋势(这是因为我截断了右边上升到无穷远的部分)，它也不像上一张图那样清晰。为了平滑损失，我们将采用指数加权平均。它的定义和SGD动量变体其实是完全相同的，对于每一个mini-batch，平均损失定义为：

$\begin{equation*} \hbox{avg loss} = \beta * \hbox{old avg loss} + (1-\beta) * \hbox{loss} \end{equation*}$

其中，$\beta$为0到1之间的参数。这样，平均损失会减少噪声，给我们一个更平滑的曲线，我们肯定能看到整体趋势。这也解释了为什么当我们在第一条曲线上达到最小值时为时已晚：当我们的损失开始爆炸时，平均损失将保持在较低的水平，而且需要一段时间才能开始真正增加。

为什么你看不到指数加权平均呢？这是因为它隐藏在我们的递归公式中，如果我们的loss是$l_{0},\dots,l_{n}$，那么第$i$个指数加权损失为：

$\begin{align*} \hbox{avg loss}_{i} &= \beta \hbox{avg loss}_{i-1} + (1-\beta) l_{i} = \beta^{2} \hbox{avg loss}_{i-2} + \beta(1-\beta) l_{i-1} + \beta l_{i} \\ &= \beta^{3} \hbox{avg loss}_{i-3} + \beta^{2}(1-\beta) l_{i-2} + \beta(1-\beta) l_{i-1} + \beta l_{i} \\ &\vdots \\ &= (1-\beta) \beta^{i} l_{0} + (1-\beta) \beta^{i-1} l_{1} + \cdots + (1-\beta) \beta l_{i-1} + (1-\beta) l_{i} \end{align*}$

权重均是$\beta$的幂。由等比求和公式，可以得到权重之和为：

$\begin{equation*} (1-\beta) \beta^{i} + (1-\beta) \beta^{i-1} + \cdots + (1-\beta) \beta + (1-\beta) = (1-\beta) * \frac{1-\beta^{i+1}}{1-\beta} = 1-\beta^{i+1} \end{equation*}$

因此，要想真正成为平均值，我们必须将平均损失除以这个因子。最后，我们要的损失是

$\begin{equation*} \hbox{smoothed loss}_{i} = \frac{\hbox{avg loss}_{i}}{1-\beta^{i+1}}. \end{equation*}$

当$i$很大时，$\beta^{i+1}$将收敛到0，但是对于$i$的第一个值，它可以确保我们获得更好的结果。

接下来还要改变一点是——我们可能不需要跑完一个epoch：如果损失开始爆发性增长，我们就不需要继续进行下去：

$\begin{equation*} \hbox{current smoothed loss} > 4 \times \hbox{minimum smoothed loss} \end{equation*}$

最后，我们仅仅需要一点点数学知识就可以计算出每一步的学习率乘积因子。如果我们初始学习率为$\hbox{lr}_{0}$，在每一步均乘上$q$，那么第$i$步学习率为：

$\begin{equation*} \hbox{lr}_{i} = \hbox{lr}_{0} \times q^{i} \end{equation*}$

现在已知初始学习率为$\hbox{lr}_{0}$，$N$步之后的学习率为$\hbox{lr}_{N-1}$，所以我们可以求解$q$：

$\begin{equation*} \hbox{lr}_{N-1} = \hbox{lr}_{0} \times q^{N-1} \quad \Longleftrightarrow \quad q^{N-1} = \frac{\hbox{lr}_{N-1}}{\hbox{lr}_{0}} \quad \Longleftrightarrow \quad q = \left ( \frac{\hbox{lr}_{N-1}}{\hbox{lr}_{0}} \right )^{\frac{1}{N-1}} \end{equation*}$

为什么要这么麻烦，而不是将学习率的初始值和最终值之间的被等间隔的分开。我们需要记住的是，我们将在画出损失随着学习率对数的曲线，如果我们取$\hbox{lr}_{i}$的对数，那么得到下式

$\begin{equation*} \log(\hbox{lr}_{i}) = \log(\hbox{lr}_{0}) + i \log(q) = \log(\hbox{lr}_{0}) + i\frac{\log(\hbox{lr}_{N-1}) - \log(\hbox{lr}_{0})}{N-1}, \end{equation*}$

上式表明，这在log尺度上我们学习率的初始值和最终值之间的被等间隔的分开。那样的话，我们的曲线上肯定会有等间距的点，通过下面式子：

$\begin{equation*} \hbox{lr}_{i} = \hbox{lr}_{0} + i \frac{\hbox{lr}_{N-1} - \hbox{lr}_{0}}{N-1} \end{equation*}$

我们的点集中在靠近末尾的地方（因为$\hbox{lr}_{N-1}$比$\hbox{lr}_{0}$大太多了）。

代码如下：

def find_lr(trn_loader, optimizer, net, criterion, init_value=1e-8, final_value=10., beta=0.98):
    """
    Args:
        trn_loader: 训练数据集的dataloader
        optimizer: 优化器
        net: 模型
        criterion: 损失函数
        init_value: float，学习率初始值
        final_value: float，学习率最终值
        beta: float，使用平滑平均计算损失时的系数

    Returns:
        log_lrs: list，从小到大的学习率
        losses: list，对应于log_lrs学习率的损失

    Note: 请根据param_groups的实际数量调整下面的初始化学习率以及更新学习率
    """
    num = len(trn_loader) - 1
    mult = (final_value / init_value) ** (1 / num)

    lr = init_value
    optimizer.param_groups[0]['lr'] = lr * 0.1
    optimizer.param_groups[1]['lr'] = lr

    avg_loss, best_loss, batch_num = 0., 0., 0
    losses, log_lrs = [], []

    tbar = tqdm.tqdm(train_loader)
    for _, inputs, labels in tbar:
        batch_num += 1

        # As before, get the loss for this mini-batch of inputs/outputs
        optimizer.zero_grad()
        outputs = net(inputs)
        loss = criterion(outputs, labels)

        # Compute the smoothed loss
        avg_loss = beta * avg_loss + (1 - beta) * loss.item()
        smoothed_loss = avg_loss / (1 - beta ** batch_num)

        # Stop if the loss is exploding
        if batch_num > 1 and smoothed_loss > 4 * best_loss:
            return log_lrs, losses

        # Record the best loss
        if smoothed_loss < best_loss or batch_num == 1:
            best_loss = smoothed_loss

        # Store the values
        losses.append(smoothed_loss)
        log_lrs.append(math.log10(lr))

        # Do the SGD step
        loss.backward()
        optimizer.step()

        # Update the lr for the next step
        lr *= mult

        # 注意我这里有两组学习率
        optimizer.param_groups[0]['lr'] = lr * 0.1
        optimizer.param_groups[1]['lr'] = lr

        params_groups_lr = str()
        for group_ind, param_group in enumerate(optimizer.param_groups):
            params_groups_lr = params_groups_lr + 'pg_%d' % group_ind + ': %.10f, ' % param_group['lr']

        descrip = params_groups_lr + 'loss： {}'.format(loss.item())
        tbar.set_description(desc=descrip)
    return log_lrs, losses

调用并画图可以采用下面代码：

log_lrs, losses = find_lr(train_loader, optimizer, model, criterion)

plt.figure(figsize=(20, 8))
plt.plot(log_lrs, losses)
# plt.plot(log_lrs[10:-5], losses[10:-5])
my_x_ticks = np.arange(-9, 1.4, 0.2)
plt.xticks(my_x_ticks)
plt.savefig('find_lr')
plt.show()

实际跑出来的结果可能如下所示：

需要记住的是，最优学习率与下降幅度最大的点有关，也就是斜率最大的地方。上面选出的optimal learning rate range可以作为一些周期性学习率变化的最大值和最小值。

学习率衰减策略

一般情况下从相对较高的学习率开始，然后在训练期间逐渐降低学习率。这种做法的直觉是使我们网络一开始快速遍历到一系列好的参数值。然后我们希望学习率足够小以便我们取探索“更深但是更窄的部分”（可以参考这里）。

Step Decay

最受欢迎的学习率衰减策略一般是Step Decay，在经过一定数量的训练后，学习速率降低一定的百分比。

更一般地说，我们可以确定，定义一个 learning rate schedule是有用的。根据这个learning rate schedule，学习率在训练期间根据特定的规则更新。

Warm up

若数据集分布和预训练权重的数据集分布较大或者没有预训练权重，建议先从较小的学习率慢慢上升到较高的学习率，然后再逐渐下降。这是因为在训练一开始，所有参数均是随机值，可能非常远离最优解。一开始就是用使用较大的学习率可能导致数值不稳定（可以参考这里）。

这两种方式的对比如下所示：

Cyclical learning rates

对于Cyclical learning rates的学习率，如下所示：

背后的主要假设是“提高学习率可能会产生短期的负面影响，但却会获得长期的好处。”事实上，Smith的论文包括了几个损失函数变化的例子，与基准固定学习率相比，损失函数暂时偏离到更高的损失，但最终收敛到更低的损失。要理解为什么这种短期效应会产生长期的积极效应，理解我们的收敛最小值的理想特性是很重要的。最后，我们希望我们的网络能够从数据中学习，并将其推广到不可见的数据中。此外，具有良好泛化属性的网络应该是健壮的，因为对网络参数的微小更改不会导致性能的急剧变化。记住这一点，这是有道理的，急剧的极小值（sharp minima）会导致不好的泛化，因为参数值的微小变化可能导致更大的损失。通过允许我们的学习速度不时增加，我们可以“跳出”急剧的最小值，这将暂时增加我们的损失，但可能最终导致收敛到一个更理想的最小值。

注意:虽然“良好泛化的平坦极小值”被广泛接受，但您可以在这里阅读一个良好的反论点。

此外，提高学习速度还可以“更快地遍历鞍点高原”。正如您在下图中所看到的，在鞍点处的梯度可能非常小。由于参数更新是梯度的函数，这导致我们的优化采取非常小的步骤；在这里增加学习率可以避免在鞍点上停留太久。

注：根据定义，鞍点是一个临界点，其中一些维度观察到局部最小值，而其他维度观察到局部最大值。因为神经网络可以有数千甚至数百万个参数，我们不太可能在所有这些维度上观察到一个真正的局部最小值；鞍点更容易出现。当提到急剧的极小值（sharp minima）时，实际上我们应该描绘一个鞍点，其中最小维度非常陡峭，而最大维度非常宽(如下图所示)。

SGD with Warm Restarts (SGDR)

与上面相似的学习率衰减策略为SGD with Warm Restarts (SGDR)：定义了一个有效的退火计划并定时“重新启动”到原始的学习率。

通过这种策略，大幅提高每次重新启动时的学习率，我们可以从本质上退出局部极小值，并继续探索损失情况。

Neat idea:：通过在每个周期结束时抓拍权重，研究人员能够根据单个模型的损失建立一个模型集合。这是因为网络从一个周期到另一个周期“settles” on various local optima，如下图所示。

总结

最常用的学习率衰减策略是StepLR，一开始可以采用ReduceLROnPlateau的学习率衰减方式确定在多少Epoch进行学习率衰减。

训练/验证曲线

在参加kaggle比赛之前，没有意识到训练/验证曲线会有多么重要，直到最近参加比赛，通过调节学习率，使得自己的名次上升了18名。下面进行一下总结：

过拟合与欠拟合

模型一旦经过训练，其真正的测试是它对以前没有见过的数据进行分类的能力，这也称为它的泛化能力。通常有两种问题会影响模型:

即使对模型进行了充分的训练，使其训练误差很小，其测试错误率仍然很高。这就是所谓的过度拟合问题。
尽管经过了几个epoch的训练，但训练损失并没有减少。这就是所谓的欠拟合问题。

欠拟合和过拟合问题在回归问题中最直观，见上图。在该图中，x表示训练数据，而曲线表示模型，它试图拟合这些数据。如图所示，拟合数据的模型有三种：最左边为直线，中间为二次多项式，最右边为6次多项式。从左图可以看出，直线并不能在训练数据中拟合曲线，导致了欠拟合（Underfitting）的问题，即使我们增加更多的训练数据也无法减少误差。而通过二次多项式来增加模型的复杂度有很大帮助，如中间图所示。另一方面，如果我们使用一个六次多项式进一步增加模型的复杂性，那么它就会适得其反，如最右图所示。在这种情况下，曲线准确地拟合了所有的训练点，但是没有拟合测试数据点，这说明了过度拟合的问题。

以下因素决定了模型从训练数据集到测试数据集的泛化程度:

模型容量及其与数据复杂度的关系：通常，如果模型容量小于数据复杂度，则会导致欠拟合；反之，则会导致过拟合。因此，我们应该尝试选择与训练和测试数据集的复杂性相匹配的模型。
即使模型容量和数据复杂度匹配得很好，我们仍然会遇到过拟合问题。这是由于训练数据不足造成的。

根据这些观察，一个有用的经验法则是：遇到过拟合问题的概率随着模型容量的增长而增加，但是随着更多的训练数据的增多而减少。注意，我们试图同时减少训练误差(以避免欠拟合问题)和测试误差(以避免过拟合问题)。这就导致了对模型容量的需求冲突，因为训练误差随着模型容量的增大而单调减小，但是当模型容量过高时，测试误差开始增大。一般情况下，如果我们绘制出测试损失值随模型容量的变化曲线，它会呈现出一个典型的U形曲线。理想的模型容量是测试误差值开始增加的点。该标准广泛用于深度学习中，以确定要使用的最佳超参数集。

上图通过画出训练和测试损失随模型容量变化的函数，说明了模型容量与欠拟合和过拟合概念之间的关系。当模型容量较低时，训练误差和测试误差都较大。随着模型容量的增大，训练误差逐渐减小，但测试误差开始减小，之后由于过拟合而测试误差开始增大。因此，最优模型容量是测试误差最小的容量。

对深度学习模型泛化能力的讨论依赖于一个非常重要的假设，即训练数据集和测试数据集可以生成相同的概率模型。在实践中，这意味着我们训练模型来识别特定类型的物体，例如人脸，如果测试数据完全由猫脸组成，我们就不能期望它表现良好。有一个著名的结果叫做“没有免费的午餐”定理：训练和测试数据集的分布是没有约束关系的，那么每个分类算法在对未观测点进行分类时的错误率是相同的。因此，更好的方法是将训练和测试数据集限制为与所解决的问题相关的更窄的一类数据。

那么如何分辨欠拟合呢？

如果一个模型表现出以下症状：它的训练损失不趋近于零，即使它训练了大量的epoch，它也显示出拟合不足的迹象。这意味着该模型的能力不够高，甚至不能以低错误概率对训练数据进行分类。也就是说，训练数据的非线性程度高于模型能够捕获的非线性程度。上图显示了一个遭受欠拟合的模型的输出示例。如图所示，训练误差和验证误差相互紧密跟踪，并且随着时间间隔的增加而趋于平缓，误差值很大。如果把训练和验证的精度绘制出来，它们也会表现出同步的扁平化行为，而只能获得较低的精度值。

为了纠正这种情况，建模者可以通过增加隐藏层的数量、为每个隐藏层添加更多的节点、更改正则化参或学习率来增加模型容量。如果这些步骤不能解决问题，那么它就指向了糟糕的训练数据。

那么如何分辨过拟合呢？

过度拟合是困扰模型的主要问题之一。当这个问题发生时，这个模型与训练数据非常吻合，但是在以前没有接触过的数据下，它不能做出很好的预测。过度拟合的原因，可以归结为模型容量与数据复杂度不匹配和或训练数据不足。模型出现以下症状时（见上图）会发生过拟合：训练数据的分类精度随epoch的增加而增加，可能接近100%，但测试精度发散或者在较低的值平缓，从而两条曲线之间有很大的差距。即训练集损失远远小于验证集损失。

我们要清楚远远大于的概念，如果训练集损失只比验证集损失多一点点的话，同等数量级(例如0.8与0.9)这种情况下并不是过拟合的表现。我们一般遇到的过拟合应该是0.8(训练集损失)与2.0(验证集损失)这种不在一个量级的损失比。

曲线分析

观察训练过程中各种参数的变化是非常重要的，首先最重要的当属损失曲线(loss curves)。

上图所示是一个比较“完美”的损失曲线变化图，在训练开始阶段损失值下降幅度很大，说明学习率合适且进行梯度下降过程，在学习到一定阶段后，损失曲线趋于平稳，损失变化没有一开始那么明显。曲线中的毛刺是因为batch-size的关系，batch-size设置越大，毛刺越小，毕竟每个batch-size的数据相当于不同的个体。

上图也是一个正确的损失曲线，虽然看到变化趋势并不是很明显，但仍然可以看出曲线在慢慢下降，这个过程其实是一个fune-turning的阶段。承接于上一幅图的损失曲线，这幅图的损失值已经很小了，虽然毛刺很多，但是总体趋势是对的。

那么什么才是有问题的去曲线呢？借用CS231n中的PPT：

上图中，左上角的图像是显然的学习不到任何东西(可能这样看起来比较困难，可以适当smooth一下)，而第二个则是典型的过拟合现象（训练loss已经很小了但是验证loss仍然很大，且不再下降）；第三个是更严重的过拟合；第四个损失值没有趋于平稳，很有可能是没有训练够；第五个经历了比较长的iterate才慢慢收敛，显然是初始化权重太小了，但是也有一种情况，那就是你的数据集中含有不正确的数据(比喻为老鼠屎)，比如猫的数据集中放了两种狗的图像，这样也会导致神经网络花费大量的时间去纠结；而最后一个越学习损失值越大，很有可能是“梯度向上”了。

上图则展示了更多的错误：左上一和二：没有对数据集进行洗牌，也就是每次训练都是采用同一个顺序对数据集进行读取（loss曲线周期性震荡）；右上一：训练的过程中突然发现曲线消失了，为什么？因为遇到了nan值(在图中是显示不出来的)，但我们要意识到这个问题，这个问题很有可能是模型设置的缘故；最后一个图显示较小比例的val集设置会导致统计不准确，比较好的val设置比例是0.2。

上图左边的曲线图可以明显看到，一共训练了五次(五条曲线)，但是在训练过程中却发现“很难”收敛，也就是神经网络学地比较困难。为什么呢？原因很简单，很有可能使我们在softmax层之前加入了非线性激活函数(比如RELU)，本来softmax函数希望我们输入负数或者正数(负数输入时Softmax期望输出比较小，而输入正数时softmax其实输出比较大)，但是relu只有正值，那么输入到softmax会造成信息的丢失，造成学习异常困难。

总结

实例分析

在我们参加kaggle比赛的一个图像分割比赛时，碰见了loss上升，同时acc(这里为dice)也在上升的情况。如下图所示：

查阅资料，可能是这样的情况：

情况一：一些边界点预测结果变得更好，他们的输出类别变了。例如一张图的正确样本为猫，之前预测结果为0.4的可能性为猫，而0.6的可能性为马。现在预测结果为0.6的可能性为猫，而0.4的可能性为马。此时，精确度增加了，而损失减少了。
情况二：假设有两类——猫和马。对于我们的例子，正确的类是马。现在，Softmax的输出为[0.9，0.1]。对于这一损失约为0.37。分类器会预测它是一匹马。以Softmax输出为[0.6，0.4]的另一种情况为例，损失约0.6。分类器仍然会预测它是一匹马，但可以肯定的是，损失增加了，而正确率不变。

当有很多样本的时候，若情况一减少的loss抵不过情况二的loss的上升，就会出现loss上升，且acc(这里为dice)也在上升的情况。说明你模型的正则化技术正在起作用，防止过拟合。此时，应该多跑一些epoch，观察loss的整体情况。

若之后loss下降，acc上升，则没有问题
若之后loss商城，acc下降，则一般情况下说明学习率比较大

总结下，如果你认为你的神经网络设计没有明显错误的，但损失曲线显示仍然很奇怪，那么很有可能：

损失函数采用的有问题
训练的数据的载入方式可能有问题
优化器(optimizer)可能有问题
一些其他的超参数设置可能有问题

总而言之，损失曲线是观察神经网络是否有问题的一大利器，我们在训练过程中非常有必要去观察我们的损失曲线的变化，越及时越好！

随机失活和权重衰减两个比较重要的超参数，这两个参数通过观察损失曲线观察是不明显滴，只有通过特定的评价标准曲线（例如图像分割中的dice指标曲线），设置好标准再进行比较，才可以判断出是否需要添加dropout或者weight decay。

标准化可能已经是训练神经网络的一个标准流程了，不论是在数据中进行标准化处理还是在网络中添加批标准化层，都是一种标准化的方法(两种使用一种即可)。

但是标准化技术通常只用于分类(以及衍生的一些应用)，但并不适合与那种对输入图像大小比较敏感以及风格迁移生成类的任务，不要问为什么，结果会给你答案..

batch-normalization的好处：https://www.learnopencv.com/batch-normalization-in-deep-networks/
相关讨论：https://www.zhihu.com/question/62599196

而我们也是通过观察准确率和损失值的曲线来判断是否需要加入标准化技术。

Learning Rate与Batch Size的关系

一般来说，越大的batch-size使用越大的学习率。

原理很简单，越大的batch-size意味着我们学习的时候，收敛方向的confidence越大，我们前进的方向更加坚定，而小的batch-size则显得比较杂乱，毫无规律性，因为相比批次大的时候，批次小的情况下无法照顾到更多的情况，所以需要小的学习率来保证不至于出错。

可以看下图损失Loss与学习率Lr的关系：

上图来源于这篇文章：Visualizing Learning rate vs Batch size

当然我们也可以从上图中看出，当batchsize变大后，得到好的测试结果所能允许的lr范围在变小，也就是说，当batchsize很小时，比较容易找打一个合适的lr达到不错的结果，当batchsize变大后，可能需要精细地找一个合适的lr才能达到较好的结果，这也给实际的large batch分布式训练带来了困难。

所以说，在显存足够的条件下，最好采用较大的batch-size进行训练，找到合适的学习率后，可以加快收敛速度。另外，较大的batch-size可以避免batch normalization出现的一些小问题：https://github.com/pytorch/pytorch/issues/4534

更多类似的问题可以在知乎找到相关答案：https://www.zhihu.com/question/64134994/answer/216895968

多尺度训练

多尺度训练是一种直接有效的方法，通过输入不同尺度的图像数据集，因为神经网络卷积池化的特殊性，这样可以让神经网络充分地学习不同分辨率下图像的特征，可以提高机器学习的性能。

也可以用来处理过拟合效应，在图像数据集不是特别充足的情况下，可以先训练小尺寸图像，然后增大尺寸并再次训练相同模型，这样的思想在Yolo-v2的论文中也提到过：

需要注意的是：多尺度训练并不是适合所有的深度学习应用，多尺度训练可以算是特殊的数据增强方法，在图像大小这一块做了调整。如果有可能最好利用可视化代码将多尺度后的图像近距离观察一下，看看多尺度会对图像的整体信息有没有影响，如果对图像信息有影响的话，这样直接训练的话会误导算法导致得不到应有的结果。例如，对于有些数据集，本身目标在图像中大小基本一致，可能不是很有效。语义分割数据集(如城市景观)包含来自不同距离的对象，因此模型必须能够检测到不同尺度的对象，所以多尺度训练效果可能较好。

PS：在我们最近参加的siim-acr-pneumothorax-segmentation比赛中，项目方提供的大小为1024；若直接训练1024，一来训练速度太慢，二来batch size太小，导致网络中的batch norm操作不能使用正确的数据统计信息，三来结果不是很好。所以，第一阶段先在768大小上进行预训练，第二阶段在1024大小上进行fine-tuing，注意的是，在第二阶段的学习率要比第一阶段的小，且优化器不需要加载第一阶段的优化器，需要重新初始化。另外，若第一阶段使用512大小的数据预训练，效果并没有在768上预训练好，可能因为768的数据统计特性更接近1024分辨率的数据统计特性。最后，第一阶段不能训练过多的epoch，否则会导致在第一阶段就过拟合了，在进行第二阶段的fine-tuing时候，跳不出局部最优解。

关于上面batchnorm操作的解释: Gradient accumulation can solve this problem, no?
It can’t because the problem is not noisy gradients but the poor statistics that the batch norm will use (this is computed on the fly during forward pass and depends on batch size). Gradient accumulation can help you get better gradients and consequently allows you to use a higher learning rate but, unfortunately, it won’t help with the batch norm issue.
Other methods of normalization such as layer norm or instance norm do not depend on the batch size (they perform normalization image-wise). However, since they are non-stochastic by design, they do not help with regularization like BN does.
Group norm, on the other hands, maintains the batch independence whilst introducing some randomness since it uses groups of channels instead of all of them, similarly to the ResNeXt architecture family.

超参数搜索

很多时候，模型搭建好了，但是随之而来的就是参数选择问题。参数选择我们一般大概分为两种方式，手动选择和自动选择。

手动选择就是我们利用对模型的理解和对结果的分析进行调参，手动选择参数，这样准确率稍高一些，但是时间长了我们会受不了，有时候真的会怀疑人生。
自动选择就是设计一个自动调参工具，让程序自己跑就行了，当然这个对机子的要求高一些，相同情况下用GPU调参速度是用CPU的几十倍。

接下来主要说一下自动选择的几个方式，程序利用Pytorch代码说明。

网格搜索

网格搜索是我们最常用的超参数调参策略。我们把每个可能的超参数组合都写下来，进行尝试：

1
2
3

style_weights = [0.1, 0.5, 1, 1.5, 2.5, 5, 10, 15, 20, 50, 100, 150, 200, 500, 1000,
                 5000, 10000, 50000, 100000, 500000, 1000000]
content_weights = [1, 5, 10, 100]

比如上面的代码，我们有两个超参数，分别是style_weight和content_weight，我们列出这些参数可能的值，然后进行训练：

1
2
3

for i in range(len(content_weights)):
    for j in range(len(style_weights)):
        output = run_painterly_transfer(cnn, cnn_normalization_mean, cnn_normalization_std, style_img=style_image,content_img=content_image, mask_img=mask_image, tmask_img=tmask_image,style_weight=int(style_weights[j]), content_weight=int(content_weights[i]))

代码很简单，通过循环将你觉得可能的参数都尝试了一遍，我们可以在程序执行的过程中把你觉得需要的中间结果和最终结果都保存到一个文件夹中，当训练完成后去查看分析即可。

整个过程就像下面的动图：

随机搜索

随机搜索就是利用分布函数来模拟随机数，然后利用随机数生成的参数来进行训练：

1
2
3

# 我们利用numpy中的随机数生成器来生成随机数
style_weights_rd = list(np.random.randint(0, 1000, size=20))
content_weights_rd = list(np.random.randint(0, 10, size=5))

同上面的参数一样，只不过换成了在特定范围的随机值，当然这个范围是我们自己定的。

然后将下面list换成随机list即可：

1
2
3

for i in range(len(content_weights_rd)):
    for j in range(len(style_weights_rd)):
        output = run_painterly_transfer(cnn, cnn_normalization_mean, cnn_normalization_std, style_img=style_image,content_img=content_image, mask_img=mask_image, tmask_img=tmask_image,style_weight=int(style_weights_rd[j]), content_weight=int(content_weights_rd[i]))

整个过程动图分析如下：

在《Random Search for Hyper-Parameter Optimization》这篇论文中提高了为什么我们经常使用随机搜索而不是用网格，其实上面的图很形象了，那就是实际中适合的参数往往在一个完整分布中的一小块部分，我们使用网络搜索并不能保证直接搜索到合适的超参数中，而随机搜索则大大提高了找到合适参数的可能性。

上图则表明重要参数和不重要的参数在不同方法下的搜索情况，我们给了两个超参数，网格搜索只能在我们设定的一小组范围内进行，而随机搜索中的每个超参数是独立的。也就是说网格搜索因为我们的设定，超参数之间是有些许联系的，并不是独一无二。研究表明随机搜索能够更快地减少验证集的误差。

下面的代码中，加入content_weight中的1和5对结果的影响不大，但是我们通过for循环组合，和style_weights中的所有值都进行了尝试了，显然浪费了时间。

1
2
3

style_weights = [0.1, 0.5, 1, 1.5, 2.5, 5, 10, 15, 20, 50, 100, 150, 200, 500, 1000,
                   5000, 10000, 50000, 100000, 500000, 1000000]
content_weights = [1, 5, 10, 100]

Cross Validation

Cross Validation) 是非常重要的一个环节。它让你知道你的 Model 有没有 Overfit，是不是真的能够 Generalize 到测试集上。在很多比赛中 Public LB 都会因为这样那样的原因而不可靠。当你改进了 Feature 或是 Model 得到了一个更高的 CV 结果，提交之后得到的 LB 结果却变差了，一般认为这时应该相信 CV 的结果。当然，最理想的情况是多种不同的 CV 方法得到的结果和 LB 同时提高，但这样的比赛并不是太多。

在数据的分布比较随机均衡的情况下，5-Fold CV 一般就足够了。如果不放心，可以提到 10-Fold。但是 Fold 越多训练也就会越慢，需要根据实际情况进行取舍。

很多时候简单的 CV 得到的分数会不大靠谱，Kaggle 上也有很多关于如何做 CV 的讨论。比如这个。但总的来说，靠谱的 CV 方法是 Case By Case 的，需要在实际比赛中进行尝试和学习，这里就不再（也不能）叙述了。

如果数据出现Label不均衡情况，可以使用Stratified K-fold，这样得到的Train Set和Test Set的Label比例是大致相同。

关键的是，随机划分结果要队伍内和方案间共享。不然的话，这个模型训练用的K折划分和那个模型训练用的K折划分不同，还怎么严格比较它们之间的优劣呢？而且这也是为后面数据分析和模型的Ensemble（集成）做准备。

交叉验证的思考：

比如分5fold，每次取一份作为验证，剩余的用于训练。由此可以得到同一个模型在不同fold上(即不同训练集上)的5个权重，对这5个权重分别在各自验证集上验证并挑选阈值，取这5个最优阈值的平均值作为最终阈值。另外，对5个权重分别对测试集进行测试，将测试结果进行平均或者依据5个权重在各自验证集上表现加权平均。如下图所示
但是折数越高，所需的运算量也较越多。

另外，我们在上面的交叉验证思考部分说了，可以将对5个权重分别对测试集进行测试，将测试结果依据5个权重在各自验证集上表现加权平均。若直接使用上面所述的CV方法不是很严谨。因为每个模型均在自己的验证集上进行评估，权重受到交叉验证划分方法的影响较大。此时，我们可以采用从整个数据集中划出一部分作为holdout set，剩余部分做交叉验证。这样最终5个权重均在这个holdout set上进行测试，评估模型的泛化能力，然后进行加权。

TTA(Test Time Augmentation)

最初这个概念是在fastai课程中看到的，这个过程在训练阶段不会参与，是通过在验证和测试阶段进行的。具体过程是，对所要处理的图像进行几种随机的图像增强变化，然后对每种图像增强后的图像进行预测，对预测结果取平均值。

原理类似于模型平均，牺牲推断速度来实现推断精度的提升。

Ensemble Generation

机器学习的模型，必不可少地对数据非常依赖。然而，如果你不知道数据服从一个什么样的分布，或者你没有办法拿到所有可能的数据（肯定拿不到所有的），那么我们训练出来的模型和真实模型之间，就会存在不一致。这种不一致表现在两个方面。

真实模型根本就没有包含在我们训练模型的模型空间中。比如本来是非线性模型，你非要拿线性模型去拟合数据，那么不论你怎么调整模型参数去选择模型，结果也是不对的。这就是偏差的来源。表现为模型不正确。
不管真实模型在不在我们训练模型的空间中，由于我们不能拿到所有可能的数据，如果拿到的数据不是那么具有代表性，那么不同的数据训练出来的模型参数就会不同。然后用这个模型去做预测，结果也就会和真实值之间有差异。这就是方差的来源。表现为模型不稳定。

用打靶的例子来说明。偏差好比你的瞄准能力；方差好比你使用的枪的性能。

瞄准的时候，正确的方式除了要考虑到三点一线，还要考虑到风向，子弹的速度和重力，距离的远近等等。如果你只会三点一线，那么就会带来偏差，因为你能力比较弱。
而枪的性能也很重要。好的枪精度高，只要你瞄的准，他都能打到瞄准点附近非常小的范围之内；而差的枪，比如你用弹弓，就算每次都瞄的准，但是它打到瞄准点附近的范围变化就比较大。

介绍完模型偏差和方差的基本概念，接着介绍模型的Ensemble Learning。

Ensemble Learning 是指将多个不同的 Base Model 组合成一个 Ensemble Model 的方法。它可以同时降低最终模型的 Bias 和 Variance（证明可以参考这篇论文)，从而在提高分数的同时又降低 Overfitting 的风险。在现在的 Kaggle 比赛中要不用 Ensemble 就拿到奖金几乎是不可能的。

常见的 Ensemble 方法有这么几种：

Bagging：使用训练数据的不同随机子集来训练每个 Base Model，最后进行每个 Base Model 权重相同的 Vote。也即 Random Forest 的原理。
Boosting：迭代地训练 Base Model，每次根据上一个迭代中预测错误的情况修改训练样本的权重。也即 Gradient Boosting 的原理。比 Bagging 效果好，但更容易 Overfit。
Blending：用不相交的数据训练不同的 Base Model，将它们的输出取（加权）平均。实现简单，但对训练数据利用少了。
Stacking：接下来会详细介绍。

从理论上讲，Ensemble 要成功，有两个要素：

Base Model 之间的相关性要尽可能的小。这就是为什么非 Tree-based Model 往往表现不是最好但还是要将它们包括在 Ensemble 里面的原因。Ensemble 的 Diversity 越大，最终 Model 的 Bias 就越低。
Base Model 之间的性能表现不能差距太大。这其实是一个 Trade-off，在实际中很有可能表现相近的 Model 只有寥寥几个而且它们之间相关性还不低。但是实践告诉我们即使在这种情况下 Ensemble 还是能大幅提高成绩。

Stacking

Stacking是用新的模型（次学习器）去学习怎么组合那些基学习器，它的思想源自于Stacked Generalization这篇论文。如果把Bagging看作是多个基分类器的线性组合，那么Stacking就是多个基分类器的非线性组合。

相比 Blending，Stacking 能更好地利用训练数据。以 5-Fold Stacking 为例，它的基本原理如图所示：

整个过程很像 Cross Validation。首先将训练数据分为 5 份，接下来一共 5 个迭代，每次迭代时，将 4 份数据作为 Training Set 对每个 Base Model 进行训练，然后在剩下一份 Hold-out Set 上进行预测。同时也要将其在测试数据上的预测保存下来。这样，每个 Base Model 在每次迭代时会对训练数据的其中 1 份做出预测，对测试数据的全部做出预测。5 个迭代都完成以后我们就获得了一个 #训练数据行数 x #Base Model 数量 的矩阵(称为out-of-fold)，这个矩阵接下来就作为第二层的 Model 的训练数据。当第二层的 Model 训练完以后，将之前保存的 Base Model 对测试数据的预测（因为每个 Base Model 被训练了 5 次，对测试数据的全体做了 5 次预测，所以对这 5 次求一个平均值，从而得到一个形状与第二层训练数据相同的矩阵，如上面第一幅图所示；当然也可以用所有的Training Data重新训练一个新模型来预测Test Data，从而得到一个形状与第二层训练数据相同的矩阵，如上面第二幅图所示）拿出来让它进行预测，就得到最后的输出。

这里给出我的实现代码：

class Ensemble(object):
    def __init__(self, n_folds, stacker, base_models):
        self.n_folds = n_folds
        self.stacker = stacker
        self.base_models = base_models

    def fit_predict(self, X, y, T):
        X = np.array(X)
        y = np.array(y)
        T = np.array(T)

        folds = list(KFold(len(y), n_folds=self.n_folds, shuffle=True, random_state=2016))

        S_train = np.zeros((X.shape[0], len(self.base_models)))
        S_test = np.zeros((T.shape[0], len(self.base_models)))

        for i, clf in enumerate(self.base_models):
            S_test_i = np.zeros((T.shape[0], len(folds)))

            for j, (train_idx, test_idx) in enumerate(folds):
                X_train = X[train_idx]
                y_train = y[train_idx]
                X_holdout = X[test_idx]
                # y_holdout = y[test_idx]
                clf.fit(X_train, y_train)
                y_pred = clf.predict(X_holdout)[:]
                S_train[test_idx, i] = y_pred
                S_test_i[:, j] = clf.predict(T)[:]

            S_test[:, i] = S_test_i.mean(1)

        self.stacker.fit(S_train, y)
        y_pred = self.stacker.predict(S_test)[:]
        return y_pred

获奖选手往往会使用比这复杂得多的 Ensemble，会出现三层、四层甚至五层，不同的层数之间有各种交互，还有将经过不同的 Preprocessing 和不同的 Feature Engineering 的数据用 Ensemble 组合起来的做法。但对于新手来说，稳稳当当地实现一个正确的 5-Fold Stacking 已经足够了。

做stacking ensemble的时候需要固定k-fold，成员之间也需要固定k-fold，否则容易出现过拟合。

XGBoost

XGBoost一直在竞赛江湖里被传为神器，比如时不时某个Kaggle/天池比赛中，某人用XGBoost于千军万马中斩获冠军。

而我们的机器学习课程里也必讲XGBoost，如寒所说：“ RF(随机森林)和GBDT(梯度提升决策树) 是工业界大爱的模型，XGBoost是大杀器包裹，Kaggle各种Top排行榜曾一度呈现XGBoost一统江湖的局面，另外某次滴滴比赛第一名的改进也少不了XGBoost的功劳”。

决策树

举个例子，集训营某一期有100多名学员，假定给你一个任务，要你统计男生女生各多少人，当一个一个学员依次上台站到你面前时，你会怎么区分谁是男谁是女呢？

很快，你考虑到男生的头发一般很短，女生的头发一般比较长，所以你通过头发的长短将这个班的所有学员分为两拨，长发的为“女”，短发为“男”。

相当于你依靠一个指标“头发长短”将整个班的人进行了划分，于是形成了一个简单的决策树，而划分的依据是头发长短。

这时，有的人可能有不同意见了：为什么要用“头发长短”划分呀，我可不可以用“穿的鞋子是否是高跟鞋”，“有没有喉结”等等这些来划分呢，答案当然是可以的。

但究竟根据哪个指标划分更好呢？很直接的判断是哪个分类效果更好则优先用哪个。所以，这时就需要一个评价标准来量化分类效果了。

怎么判断“头发长短”或者“是否有喉结”是最好的划分方式，效果怎么量化呢？直观上来说，如果根据某个标准分类人群后，纯度越高效果越好，比如说你分为两群，“女”那一群都是女的，“男”那一群全是男的，那这个效果是最好的。但有时实际的分类情况不是那么理想，所以只能说越接近这种情况，我们则认为效果越好。

量化分类效果的方式有很多，比如信息增益（ID3）、信息增益率（C4.5）、基尼系数（CART）等等。

这里介绍下信息增益的度量标准：熵

ID3算法的核心思想就是以信息增益度量属性选择，选择分裂后信息增益最大的属性进行分裂。

什么是信息增益呢？为了精确地定义信息增益，我们先定义信息论中广泛使用的一个度量标准，称为熵（entropy），它刻画了任意样例集的纯度（purity）。给定包含关于某个目标概念的正反样例的样例集S，那么S相对这个布尔型分类的熵为：

$Entropy(s)=-p_{\oplus}log_2p_{\oplus}-p_{\ominus}log_2p_{\ominus}$

在上式中，$p_{\oplus}$代表正样例，比如在本文开头第二个例子中代表男生，而$p_{\ominus}$表示负样例，女生。在有关熵的计算中所有$0log0=0$。

举例来说，假设S是一个关于布尔概念的有14个样例的集合，它包括9个正例和5个反例（我们采用记号[9+，5-]来概括这样的数据样例），那么S相对于这个布尔样例的熵为：

$Entropy（[9+，5-]）=-（9/14）log_2（9/14）-（5/14）log_2（5/14）=0.940$

So，根据上述这个公式，我们可以得到：

如果S的所有成员属于同一类，则$Entropy(S)=0$；
如果S的正反样例数量相等，则$Entropy(S)=1$；
如果S的正反样例数量不等，则熵介于0，1之间

看到没，通过Entropy的值，你就能评估当前分类树的分类效果好坏了。

更多细节如剪枝、过拟合、优缺点、可以参考此文决策树学习。

所以，现在决策树的灵魂已经有了，即依靠某种指标进行树的分裂达到分类/回归的目的，总是希望纯度越高越好。

回归树与集成学习

如果用一句话定义XGBoost，很简单：XGBoost就是由很多CART树集成。但，什么是CART树？

数据挖掘或机器学习中使用的决策树有两种主要类型：

分类树分析是指预测结果是数据所属的类（比如某个电影去看还是不看）
回归树分析是指预测结果可以被认为是实数（例如房屋的价格，或患者在医院中的逗留时间）

而术语分类回归树（CART，Classification And Regression Tree）分析是用于指代上述两种树的总称，由Breiman等人首先提出。

回归树

事实上，分类与回归是两个很接近的问题，分类的目标是根据已知样本的某些特征，判断一个新的样本属于哪种已知的样本类，它的结果是离散值。而回归的结果是连续的值。当然，本质是一样的，都是特征（feature）到结果/标签（label）之间的映射。

理清了什么是分类和回归之后，理解分类树和回归树就不难了。

分类树的样本输出（即响应值）是类的形式，比如判断这个救命药是真的还是假的，周末去看电影《风语咒》还是不去。而回归树的样本输出是数值的形式，比如给某人发放房屋贷款的数额就是具体的数值，可以是0到300万元之间的任意值。

所以，对于回归树，你没法再用分类树那套信息增益、信息增益率、基尼系数来判定树的节点分裂了，你需要采取新的方式评估效果，包括预测误差（常用的有均方误差、对数误差等）。而且节点不再是类别，是数值（预测值），那么怎么确定呢？有的是节点内样本均值，有的是最优化算出来的比如XGBoost。

CART回归树是假设树为二叉树，通过不断将特征进行分裂。比如当前树结点是基于第$j$个特征值进行分裂的，设该特征值小于$s$的样本划分为左子树，大于$s$的样本划分为右子树。

$R_{1}(j, s)=\left\{x | x^{(j)} \leq s\right\} \text { and } R_{2}(j, s)=\left\{x | x^{(j)}>s\right\}$

而CART回归树实质上就是在该特征维度对样本空间进行划分，而这种空间划分的优化是一种NP难问题，因此，在决策树模型中是使用启发式方法解决。典型CART回归树产生的目标函数为：

$\sum_{x_{i} \in R_{m}}\left(y_{i}-f\left(x_{i}\right)\right)^{2}$

因此，当我们为了求解最优的切分特征$j$和最优的切分点$s$，就转化为求解这么一个目标函数：

$\min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right]$

所以我们只要遍历所有特征的的所有切分点，就能找到最优的切分特征和切分点。最终得到一棵回归树。

这里的特征可以理解为数据的属性，比如说，一个人身高体重等。

boosting集成学习

所谓集成学习，是指构建多个分类器（弱分类器）对数据集进行预测，然后用某种策略将多个分类器预测的结果集成起来，作为最终预测结果。通俗比喻就是“三个臭皮匠赛过诸葛亮”，或一个公司董事会上的各董事投票决策，它要求每个弱分类器具备一定的“准确性”，分类器之间具备“差异性”。

集成学习根据各个弱分类器之间有无依赖关系，分为Boosting和Bagging两大流派：

Boosting流派，各分类器之间有依赖关系，必须串行，比如Adaboost、GBDT(Gradient Boosting Decision Tree)、XGBoost
Bagging流派，各分类器之间没有依赖关系，可各自并行，比如随机森林（Random Forest）

著名的Adaboost作为boosting流派中最具代表性的一种方法，下面详细介绍它。

AdaBoost，是英文”Adaptive Boosting”（自适应增强）的缩写，由Yoav Freund和Robert Schapire在1995年提出。它的自适应在于：前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器。同时，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。

具体说来，整个Adaboost 迭代算法就3步：

初始化训练数据的权值分布。如果有N个样本，则每一个训练样本最开始时都被赋予相同的权值：1/N。
训练弱分类器。具体训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。然后，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。换言之，误差率低的弱分类器在最终分类器中占的权重较大，否则较小。

而另一种boosting方法GBDT（Gradient Boost Decision Tree)，则与AdaBoost不同，GBDT每一次的计算是都为了减少上一次的残差，进而在残差减少（负梯度）的方向上建立一个新的模型。

boosting集成学习由多个相关联的决策树联合决策，什么叫相关联？举个例子

有一个样本[数据->标签]是：[(2，4，5)-> 4]，第一棵决策树用这个样本训练的预测为3.3，那么第二棵决策树训练时的输入，这个样本就变成了：[(2，4，5)-> 0.7]，也就是说，下一棵决策树输入样本会与前面决策树的训练和预测相关。

之所以第二次输入标签变成了0.7，是因为要将所有弱分类器的结果相加，第一个弱分类器预测出的结果为3.3，第二个弱分类器则需要预测第一个分类器与真实值之间的差值，即为0.7。

很快你会意识到，XGBoost为何也是一个boosting的集成学习了。

而一个回归树形成的关键点在于：

分裂点依据什么来划分（如前面说的均方误差最小，loss）；
分裂后的节点预测值是多少（如前面说，有一种是将叶子节点下各样本实际值的均值作为叶子节点预测误差，或者计算所得）

至于另一类集成学习方法，比如Random Forest（随机森林）算法，各个决策树是独立的、每个决策树在样本堆里随机选一批样本，随机选一批特征进行独立训练，各个决策树之间没有啥关系。本文暂不展开介绍。

GBDT

说到XGBoost，不得不先从GBDT(Gradient Boosting Decision Tree)说起。因为XGBoost本质上还是一个GBDT，但是力争把速度和效率发挥到极致，所以叫X (Extreme) GBoosted。包括前面说过，两者都是boosting方法。

GBDT的原理很简单，就是所有弱分类器的结果相加等于预测值，然后下一个弱分类器去拟合误差函数对预测值的梯度/残差(这个梯度/残差就是预测值与真实值之间的误差)。当然了，它里面的弱分类器的表现形式就是各棵树。如图所示：$Y = Y1 + Y2 + Y3$。

举一个非常简单的例子，比如我今年30岁了，但计算机或者模型GBDT并不知道我今年多少岁，那GBDT咋办呢？

它会在第一个弱分类器（或第一棵树中）随便用一个年龄比如20岁来拟合，然后发现误差有10岁；
接下来在第二棵树中，用6岁去拟合剩下的损失，发现差距还有4岁；
接着在第三棵树中用3岁拟合剩下的差距，发现差距只有1岁了；
最后在第四课树中用1岁拟合剩下的残差，完美。

最终，四棵树的结论加起来，就是真实年龄30岁。实际工程中，GBDT是计算负梯度，用负梯度近似残差。

注意，为何GBDT可以用用负梯度近似残差呢？

回归任务下，GBDT 在每一轮的迭代时对每个样本都会有一个预测值，此时的损失函数为均方差损失函数，

$l\left(y_{i}, y^{i}\right)=\frac{1}{2}\left(y_{i}-y^{i}\right)^{2}$ $-\left[\frac{\partial l\left(y_{i}, y^{i}\right)}{\partial y^{i}}\right]=\left(y_{i}-y^{i}\right)$

所以，当损失函数选用均方损失函数是时，每一次拟合的值就是（真实值-当前模型预测的值），即残差。此时的变量是$y^{i}$，即“当前预测模型的值”，也就是对它求负梯度。

另外，这里还得再啰嗦一下，上面预测年龄的第一个步骤中的“随便”二字看似随便，其实深入思考一下一点都不随便，你会发现大部分做预测的模型，基本都是这么个常规套路，先随便用一个值去预测，然后对比预测值与真实值的差距，最后不断调整缩小差距。所以会出来一系列目标函数：确定目标，和损失函数：缩小误差。

再进一步思考，你会发现这完全符合人类做预测的普遍常识、普遍做法，当对一个事物不太了解时，一开始也是根据经验尝试、初探，直到逼近某种意义上的接近或者完全吻合。

还是年龄预测的例子。

简单起见，假定训练集只有4个人：A,B,C,D，他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生；C,D分别是应届毕业生和工作两年的员工。

所以，现在的问题就是我们要预测这4个人的年龄，咋下手？很简单，先随便用一个年龄比如20岁去拟合他们，然后根据实际情况不断调整。

如果是用一棵传统的回归决策树来训练，会得到如下图所示结果：

现在我们使用GBDT来做这件事，由于数据太少，我们限定叶子节点做多有两个，即每棵树都只有一个分枝，并且限定只学两棵树。

我们会得到如下图所示结果：

在第一棵树分枝和图1一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为左右两拨，每拨用平均年龄作为预测值。

此时计算残差（残差的意思就是：A的实际值 - A的预测值 = A的残差），所以A的残差就是实际值14 - 预测值15 = 残差值-1。
注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值。
残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话，我们可以将残差看作误差的观测值。

进而得到A,B,C,D的残差分别为-1,1，-1,1。

然后拿它们的残差-1、1、-1、1代替A B C D的原值，到第二棵树去学习，第二棵树只有两个值1和-1，直接分成两个节点，即A和C分在左边，B和D分在右边，经过计算（比如A，实际值-1 - 预测值-1 = 残差0，比如C，实际值-1 - 预测值-1 = 0），此时所有人的残差都是0。

残差值都为0，相当于第二棵树的预测值和它们的实际值相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了，即每个人都得到了真实的预测值。

换句话说，现在A,B,C,D的预测值都和真实年龄一致了。Perfect！

A: 14岁高一学生，购物较少，经常问学长问题，预测年龄A = 15 – 1 = 14
B: 16岁高三学生，购物较少，经常被学弟问问题，预测年龄B = 15 + 1 = 16
C: 24岁应届毕业生，购物较多，经常问师兄问题，预测年龄C = 25 – 1 = 24
D: 26岁工作两年员工，购物较多，经常被师弟问问题，预测年龄D = 25 + 1 = 26

所以，GBDT需要将多棵树的得分累加得到最终的预测得分，且每一次迭代，都在现有树的基础上，增加一棵树去拟合前面树的预测结果与真实值之间的残差。

XGBoost

XGBoost树的定义

本节的示意图基本引用自XGBoost原作者陈天奇的讲义PPT中。

举个例子，我们要预测一家人对电子游戏的喜好程度，考虑到年轻和年老相比，年轻更可能喜欢电子游戏，以及男性和女性相比，男性更喜欢电子游戏，故先根据年龄大小区分小孩和大人，然后再通过性别区分开是男是女，逐一给各人在电子游戏喜好程度上打分，如下图所示。

就这样，训练出了2棵树tree1和tree2，类似之前GBDT的原理，两棵树的结论累加起来便是最终的结论，所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加：2 + 0.9 = 2.9。爷爷的预测分数同理：-1 + （-0.9）= -1.9。具体如下图所示

恩，你可能要拍案而起了，惊呼，这不是跟上文介绍的GBDT乃异曲同工么？

事实上，如果不考虑工程实现、解决问题上的一些差异，XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示：

红色箭头所指向的L 即为损失函数，比如平方损失函数：$l\left(y_{i}, y^{i}\right)=\left(y_{i}-y^{i}\right)^{2}$，或logistic损失函数：$l\left(y_{i}, \hat{y}_{i}\right)=y_{i} \ln \left(1+e^{-\hat{y}_{i}}\right)+\left(1-y_{i}\right) \ln \left(1+e^{\hat{y}_{i}}\right)$
红色方框所框起来的是正则项（包括L1正则、L2正则）
红色圆圈所圈起来的为常数项
对于$f(x)$，XGBoost利用泰勒展开三项，做一个近似

我们可以很清晰地看到，最终的目标函数只依赖于每个数据点在误差函数上的一阶导数和二阶导数。

额，峰回路转，突然丢这么大一个公式，不少人可能瞬间就懵了。没事，下面咱们来拆解下这个目标函数，并一一剖析每个公式、每个符号、每个下标的含义。

XGBoost目标函数

XGBoost的核心算法思想不难，基本就是

1.不断地添加树，不断地进行特征分裂来生长一棵树，每次添加一个树，其实是学习一个新函数，去拟合上次预测的残差。

$\hat{y}=\phi\left(x_{i}\right)=\sum_{k=1}^{K} f_{k}\left(x_{i}\right)$ $F=\left\{f(x)=w_{q(x)}\right\}\left(q : R^{m} \rightarrow T, w \in R^{T}\right)$

注：$w_q(x)$为叶子节点$q$的分数，$\mathcal{F}$对应了所有$K$棵回归树（regression tree）的集合，而$f(x)$为其中一棵回归树。

2.当我们训练完成得到$k$棵树，我们要预测一个样本的分数，其实就是根据这个样本的特征，在每棵树中会落到对应的一个叶子节点，每个叶子节点就对应一个分数。

3.最后只需要将每棵树对应的分数加起来就是该样本的预测值。

显然，我们的目标是要使得树群的预测值$\hat{y}_{i}$尽量接近真实值$y_{i}$，而且有尽量大的泛化能力。

所以，从数学角度看这是一个泛函最优化问题，故把目标函数简化如下：

$L(\phi)=\sum_{i} l\left(\hat{y}_{i}-y_{i}\right)+\sum_{k} \Omega\left(f_{k}\right)$

如你所见，这个目标函数分为两部分：损失函数和正则化项。且损失函数揭示训练误差（即预测分数和真实分数的差距），正则化定义复杂度。

对于上式而言，$\hat{y}_{i}$是整个累加模型的输出，正则化项$\sum_{k} \Omega\left(f_{k}\right)$是则表示树的复杂度的函数，值越小复杂度越低，泛化能力越强，其表达式为

$\Omega(f)=\gamma T+\frac{1}{2} \lambda\|w\|^{2}$

$T$表示叶子节点的个数，$w$表示叶子节点的分数。直观上看，目标要求预测误差尽量小，且叶子节点$T$尽量少（$γ$控制叶子结点的个数），节点数值$w$尽量不极端（$λ$控制叶子节点的分数不会过大），防止过拟合。

插一句，一般的目标函数都包含下面两项

其中，误差/损失函数鼓励我们的模型尽量去拟合训练数据，使得最后的模型会有比较少的 bias。而正则化项则鼓励更加简单的模型。因为当模型简单之后，有限数据拟合出来结果的随机性比较小，不容易过拟合，使得最后模型的预测更加稳定。

未完待续…

附件

文章中的visio图的附件在这里

参考

如何在 Kaggle 首战中进入前 10%
分分钟带你杀入Kaggle Top 1%
为什么做stacking ensemble的时候需要固定k-fold？
Kaggle数据挖掘比赛经验分享，陈成龙博士整理！
通俗理解kaggle比赛大杀器xgboost
如何根据训练/验证损失曲线诊断我们的CNN
浅谈深度学习中超参数调整策略
 关于训练神经网路的诸多技巧Tricks(完全总结版)
How to interpret increase in both loss and accuracy
How is it possible that validation loss is increasing while validation accuracy is increasing as well
Kaggle求生：亚马逊热带雨林篇
 cross-validation：从 holdout validation 到 k-fold validation
Gradient accumulation can solve this problem, no?
pretrain weight dicusses
How Do You Find A Good Learning Rate
寻找最优学习率的方法以及周期性学习率更新策略(论文笔记)
神经网络学习速率设置指南（CLR Callback，LRFinder，SGDR等最新的学习率设置方案）附完整代码解析
 Setting the learning rate of your neural network.
Chapter 7 Training Neural Networks Part 1
Chapter 8 Training Neural Networks Part 2
机器学习算法如何调参？这里有一份神经网络学习速率设置指南
 模型的偏差与方差的理解