zdaiot

404NotFound

图像分割评价指标

发表于 更新于 分类于 ，
本文字数： 6.4k 阅读时长 ≈ 6 分钟

最近做了一些关于图像分割的任务，但是对于如何评价图像分割的好坏，之前自己并没有一个很深刻的了解。今天上午对这些指标进行一个总结。

图像分割中通常使用许多标准来衡量算法的精度。这些标准通常是像素精度及IoU的变种，以下我们将会介绍常用的几种逐像素标记的精度标准。为了便于解释，假设如下：共有$k+1$个类（从$L_0$到$L_k$，其中包含一个空类或背景），$p_{ij}$表示本属于类$i$但被预测为类$j$的像素数量。即$p_{ii}$表示真正的数量，而$p_{ij}, p_{ji}$则分别被解释为假正和假负，尽管两者分别为假正与假负数量之和。

基础知识

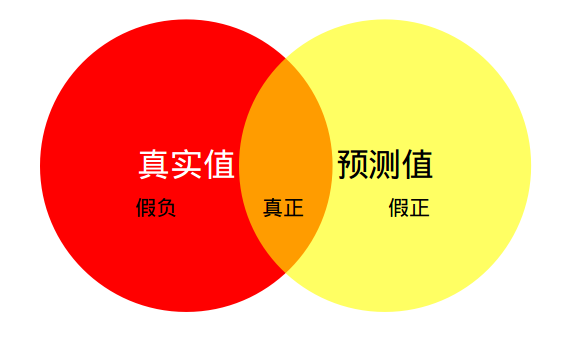
如下图所示，红色圆代表真实值，黄色圆代表预测值。橙色部分红色圆与黄色圆的交集，即真正（预测为1，真实值为1）的部分，红色部分表示假负（预测为0，真实为1）的部分，黄色表示假正（预测为1，真实为0）的部分，两个圆之外的白色区域表示真负（预测为0，真实值为0）的部分。

如何理解上面在说明真正、假负、假正、真负时用到的0和1呢？这个我觉得这么解释可能更加清晰。

  • 真正（TP）：真实为这个类，预测结果也为这个类，即橙色部分。预测正确（True），预测为了正样本（positive）；真的正值，说明被预测为正样本，预测是真的，即真实值为正样本
  • 假负（FN）：真正为这个类，预测结果不是这个类，即红色部分。预测错了（False），预测为了负样本（negative）；假的负值，说明被预测为负样本，但预测是假的，即真实值为正样本
  • 假正（FP）：真正不是这个类，预测结果为这个类，即黄色部分。预测错了（False），预测为了正样本（positive）；假的正直：说明被预测为正样本，但预测是假的，即真实值为负样本
  • 真负（TN）：真正不是这个类，预测结果不是这个类，即白色部分。预测正确（True），预测为了负样本（negative）；真的负值，说明被预测为负样本，预测是真的，即真实值为负样本

precesion

针对预测样本而言，预测为正例的样本中真正为真样本的比例：
预测为正的有两种：
1、正样本被预测为正 TP
2、负样本被预测为正 FP

所以精确率：

其中分母预测为正样本数量。

recall

针对原来的样本而言，表示样本中有多少正例被预测正确了（预测为正例的占所有真实正例的比例）：
1、原来的正样本被预测为正样本 TP
2、原来的正样本被预测为负样本 FN

所以召回率为：

其中分母表示原来样本中的正样本数量。

PA

Pixel Accuracy(PA，像素精度)：这是最简单的度量，为标记正确的像素占总像素的比例。

如何理解这个分母 呢？

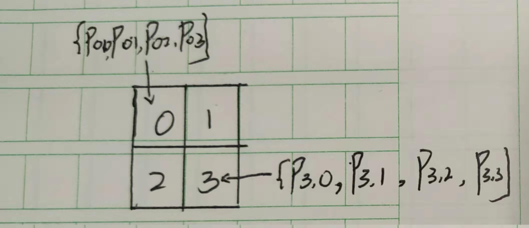
如下图所示，对于一张图片一共有{0，1，2，3}4类，对于第0类，其分类情况有4种分别为{$p_{00},p_{01},p_{02},p_{03}$}，同理对于第1，2，3类均有4种情况，这也就对应了分母中的两次求和。

对于样本不均衡的情况，例如医学图像分割中，背景与标记样本之间的比例往往严重失衡。因此并不适合使用这种方法进行度量。

MPA

Mean Pixel Accuracy(MPA，均像素精度)：是PA的一种简单提升，计算每个类内被正确分类像素数的比例，之后求所有类的平均。

MIoU

Mean Intersection over Union(MIoU，均交并比)：为语义分割的标准度量。其计算两个集合的交集和并集之比，在语义分割的问题中，这两个集合为真实值（ground truth）和预测值（predicted segmentation）。这个比例可以变形为正真数（intersection）比上真正、假负、假正（并集）之和。在每个类上计算IoU，之后平均。

那么，如何理解这里的公式呢？如下图所示，红色圆代表真实值，黄色圆代表预测值。橙色部分红色圆与黄色圆的交集，即真正（预测为1，真实值为1）的部分，红色部分表示假负（预测为0，真实为1）的部分，黄色表示假正（预测为1，真实为0）的部分，两个圆之外的白色区域表示真负（预测为0，真实值为0）的部分。

  • MP计算橙色与（橙色与红色）的比例。
  • MIoU计算的是计算A与B的交集（橙色部分）与A与B的并集（红色+橙色+黄色）之间的比例，在理想状态下A与B重合，两者比例为1 。

FWIoU

Frequency Weighted Intersection over Union(FWIoU，频权交并比):为MIoU的一种提升，这种方法根据每个类出现的频率为其设置权重。

其中，$\sum_{i=0}^{k}{\sum_{j=0}^{k}{p_{ij}}}$即为所有类的像素总数。$\sum_{j=0}^{k}{p_{ij}}$为真实情况下属于第$i$类的像素总数。$\sum_{j=0}^{k}{p_{ji}}$即为预测为第$i$类的像素总数。

在以上所有的度量标准中，MIoU由于其简洁、代表性强而成为最常用的度量标准，大多数研究人员都使用该标准报告其结果。PA对于样本不均衡的情况不适用。

DICE

DICE与IOU很相似，具体两者的区别如下：

从中可以看出，$\text{DC} \geq \text{IoU}$（两者相减得到的式子中分子为$|X| + |Y| - 2|X \cap Y|$，显然分子大于0）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
import _init_paths

import os
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from skimage import io
from timer import Timer
import cv2
from datetime import datetime

import caffe

test_file = 'test.txt'
file_path_img = 'JPEGImages'
file_path_label = 'SegmentationClass'
save_path = 'output/results'

test_prototxt = 'Models/test.prototxt'
weight = 'Training/Seg_iter_10000.caffemodel'

layer = 'conv_seg'
save_dir = False # True

if save_dir:
    save_dir = save_path
else:
    save_dir = False

# load net
net = caffe.Net(test_prototxt, weight, caffe.TEST)

# load test.txt
test_img = np.loadtxt(test_file, dtype=str)

def fast_hist(a, b, n):
    k = (a >= 0) & (a < n)
    return np.bincount(n * a[k].astype(int) + b[k], minlength=n**2).reshape(n, n)

# seg test
print '>>>', datetime.now(), 'Begin seg tests'

n_cl = net.blobs[layer].channels
hist = np.zeros((n_cl, n_cl))

# timers
_t = {'im_seg' : Timer()}

# load image and label
i = 0
for img_name in test_img:
    _t['im_seg'].tic()
    img = Image.open(os.path.join(file_path_img, img_name + '.jpg'))
    img = img.resize((512, 384), Image.ANTIALIAS)

    in_ = np.array(img, dtype=np.float32)
    in_ = in_[:,:,::-1] # rgb to bgr
    in_ -= np.array([[[68.2117, 78.2288, 75.4916]]])#数据集平均值，根据需要修改
    in_ = in_.transpose((2,0,1))

    label = Image.open(os.path.join(file_path_label, img_name + '.png'))
    label = label.resize((512, 384), Image.ANTIALIAS)#图像大小（宽，高），根据需要修改
    label = np.array(label, dtype=np.uint8)

    # shape for input (data blob is N x C x H x W), set data
    net.blobs['data'].reshape(1, *in_.shape)
    net.blobs['data'].data[...] = in_

    net.forward()
    _t['im_seg'].toc()

    print 'im_seg: {:d}/{:d} {:.3f}s' \
          .format(i + 1, len(test_img), _t['im_seg'].average_time)
    i += 1

    hist += fast_hist(label.flatten(), net.blobs[layer].data[0].argmax(0).flatten(), n_cl)

    if save_dir:
        seg = net.blobs[layer].data[0].argmax(axis=0)
        result = np.array(img, dtype=np.uint8)
        index = np.where(seg == 1)
        for i in xrange(len(index[0])):
            result[index[0][i], index[1][i], 0] =  255
            result[index[0][i], index[1][i], 1] =  0
            result[index[0][i], index[1][i], 2] =  0
        result = Image.fromarray(result.astype(np.uint8))    
        result.save(os.path.join(save_dir, img_name + '.jpg'))        

iter = len(test_img)
# overall accuracy
acc = np.diag(hist).sum() / hist.sum()
print '>>>', datetime.now(), 'Iteration', iter, 'overall accuracy', acc
# per-class accuracy
acc = np.diag(hist) / hist.sum(1)
print '>>>', datetime.now(), 'Iteration', iter, 'mean accuracy', np.nanmean(acc)
# per-class IU
iu = np.diag(hist) / (hist.sum(1) + hist.sum(0) - np.diag(hist))
print '>>>', datetime.now(), 'Iteration', iter, 'mean IU', np.nanmean(iu)
freq = hist.sum(1) / hist.sum()
print '>>>', datetime.now(), 'Iteration', iter, 'fwavacc', \
    (freq[freq > 0] * iu[freq > 0]).sum()

疑惑

为何不适用MPA，而使用MIOU，两者在什么情况下有区别～

参考

论文笔记 |　基于深度学习的图像语义分割技术概述之5.1度量标准
图像分割的衡量指标详解
Image Segmentation Evaluation
Losses for Image Segmentation

------ 本文结束------
坚持原创技术分享，您的支持将鼓励我继续创作！

欢迎关注我的其它发布渠道