之前一直觉得一些平台上的博客比较优秀,真的是作者经过思考。例如当我查到一些文章的时候,若同时来在于CSDN、知乎、简书、CMD Markdown。那么我会看的顺序则为CMD Markdown > 简书 > 知乎 > CSDN。尤其是CSDN,基本都是照抄。虽然我也照抄。。最近在做图像分割的比赛。因为遇到了瓶颈,不能再停留在表面了,需要深挖一下内部原理。看到CMD Markdown上有一篇文章不错,特来照抄一下。
本文翻译自An overview of semantic image segmentation,原作者保留版权。
这篇文章讲述卷积神经网络在图像语义分割(semantic image segmentation)的应用。图像分割这项计算机视觉任务需要判定一张图片中特定区域的所属类别。
这个图像里有什么?它在图像中哪个位置?
更具体地说,图像语义分割的目标是将图像的每个像素所属类别进行标注。因为我们是预测图像中的每个像素,这个任务通常被称为密集预测(dense prediction)。如下图所示

需要注意的一点是我们不对同一类的实例进行分离; 我们只关心每个像素的类别。 换句话说,如果输入图像中有两个相同类别的对象,则分割图本身并不一定将它们区分为单独的对象。 存在另外一类不同的模型,称为实例分割(instance segmentation)模型,其将分离同一类的各个对象。
分割模型广泛应用在各领域中,包括:
- 自动驾驶(Autonomous vehicles):汽车需要安装必要的感知系统以了解它们的环境,这样自动驾驶汽车才能够安全地驶入现有的道路。

医疗影像诊断(Medical image diagnostics):机器在分析能力上比放射科医生更强,而且可以大大减少诊断所需时间。
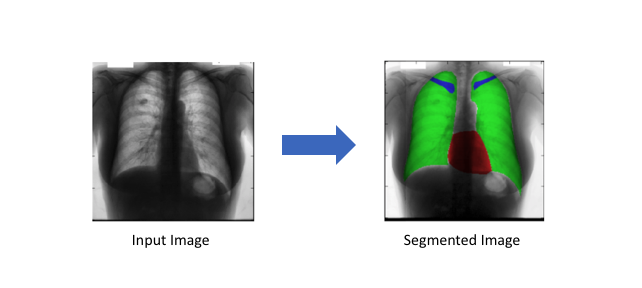
任务描述
简单来说,我们的目标是输入一个RGB彩色图片($height\times width\times 3$)或者一个灰度图($height\times width\times 1$),然后输出一个包含各个像素类别标签的分割图($height\times width\times 1$)。
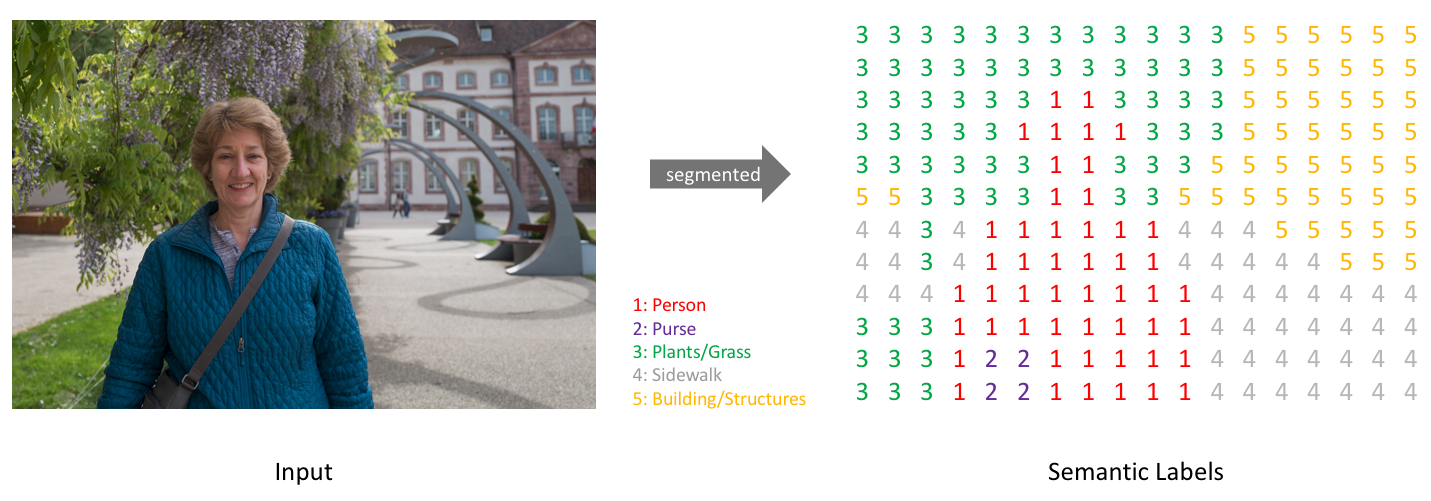
与我们处理标准分类值的方式类似,我们的预测目标可以采用one-hot编码,即为每一个可能的类创建一个输出通道。通过取每个像素点在各个channel的argmax可以得到最终的预测分割图(如下图所示)。
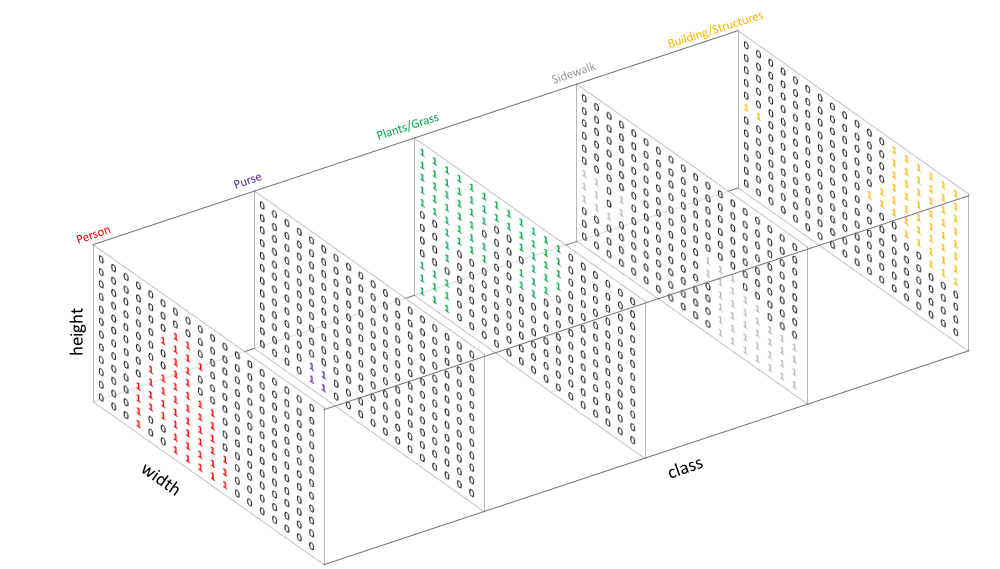
我们可以将分割图叠加到原始图像上可以检验分割效果。当我们将预测结果叠加到单个channel时,称这为一个mask,它可以给出一张图像中某个特定类的所在区域。

架构设计
对于图像语义分割任务,构建神经网络架构的一种简单方法是简单地堆叠多个卷积层(使用same padding以维持维度大小)并输出最终的分割图。 这通过特征映射的连续变换直接学习从输入图像到其对应分割的映射关系;但是,在整个网络中保持图像原始分辨率的计算成本非常高。如下图所示。网络缺点:在整个网络中维持图像原始维度计算成本很高(来源:cs231n)
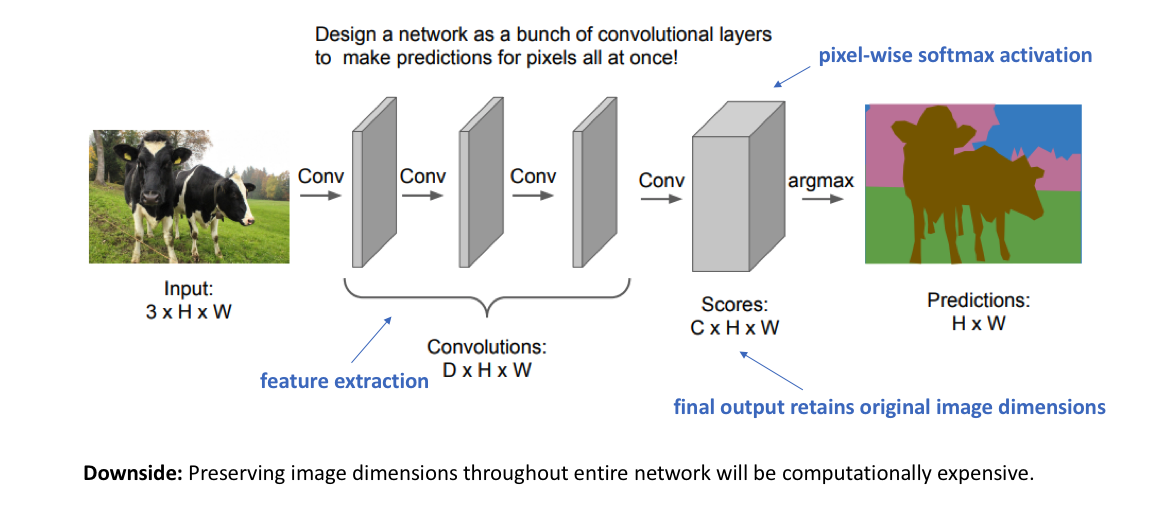
回想一下,对于深度卷积网络,前面的层倾向于学习低级特征,而后面的层学习更高级的特征映射。为了保持表现力,我们通常需要在网络更深时增加特征图(channels)的数量。
对于图像分类问题,增加特征图(channels)数量不一定造成问题,因为对于该任务,我们只关心图像中包含的物体(而不是它所在的位置)。 因此,我们可以通过通过池化或跨步卷积(即压缩空间分辨率)周期性地对特征图进行下采样来减轻计算量。然而,对于图像分割,我们希望模型最后给出全分辨率的语义预测。
用于图像分割模型的一种流行方法是遵循编码器/解码器(encoder/decoder)结构,其中我们先对输入进行下采样(downsample),得到较低分辨率的特征映射,其学习到了如何高效地区分各个类,然后对这些特征进行上采样(upsample)以得到一个全分辨率分割图。
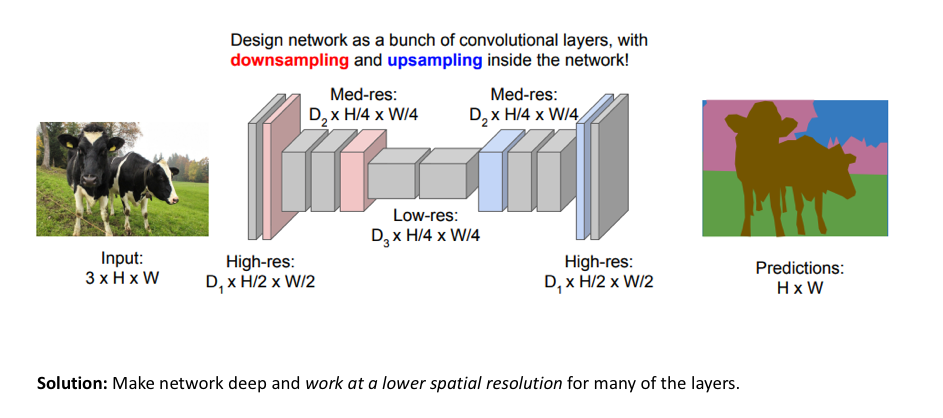
上采样(upsampling)方法
可以采用不同的方法来上采样以提高特征图的分辨率。 pooling操作聚合一个局部区域(平均或最大池化)来下采样,相对应地,unpooling操作通过将单个值分配到更高的分辨率来上采样。
然而目前为止最流行的方法是转置卷积(transpose convolutions),因为它是通过学习得到的上采样方法。转置卷积(transpose convolution)也被称为分数步长卷积(convolution with fractional strides)或者反卷积或者后向卷积backwards strided convolution。
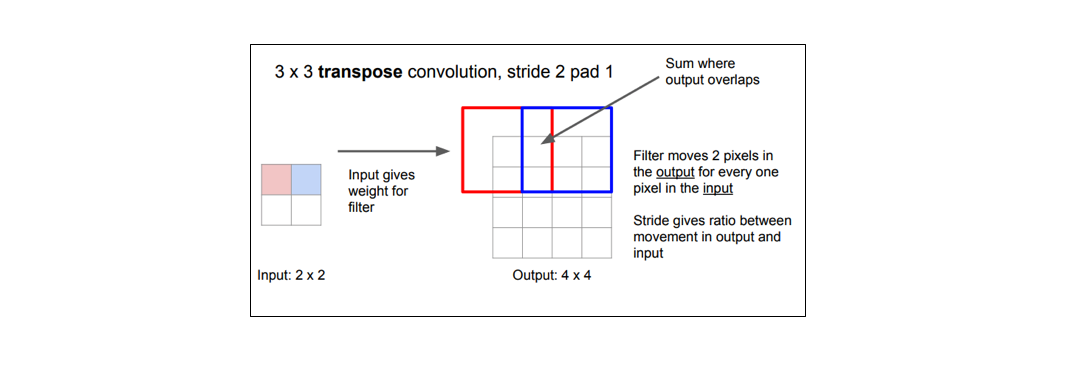
而典型的卷积运算将视野中所有值求点积并在相应位置输出单个值,而转置卷积恰恰相反。对于转置卷积,低分辨率特征图中某个值,乘以卷积核中的权重值,将这些加权值映射到输出特征图。如下图为1D转置卷积的简化实例。

某些卷积核可能在输出特征图中产生重叠(例如$stride=2$的$3\times3$卷积, 如下图所示),此时重叠值就简单地加在一起。 不好的是,这往往会在输出中形成棋盘效应(不均匀重叠,可以参考Deconvolution and Checkerboard Artifacts),这是不希望被看到的,因此最好确保选择的卷积核不会导致重叠。如下图为步长为2的3x3转置卷积,其中上面输入,下面是输出。(来源:https://github.com/vdumoulin/conv_arithmetic)
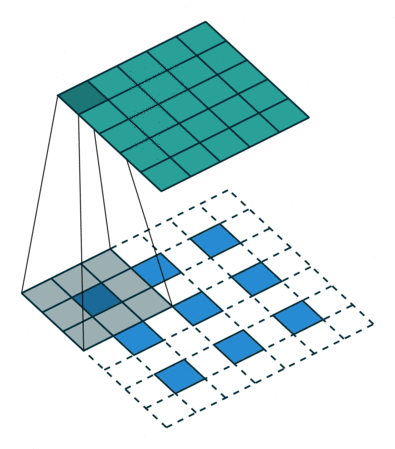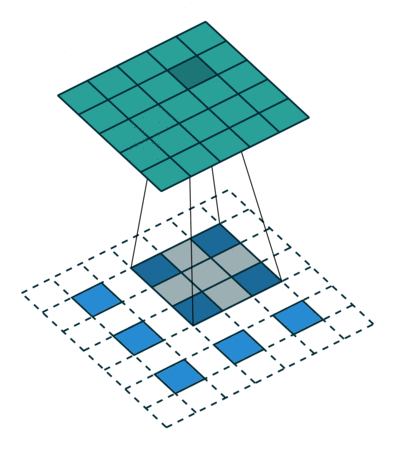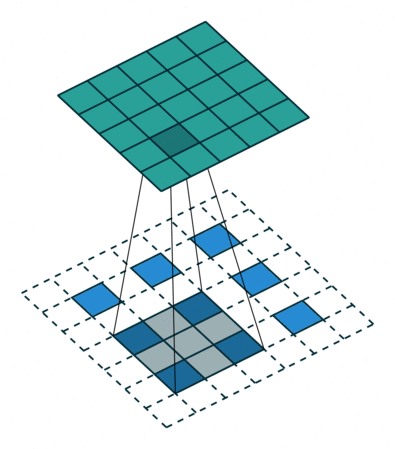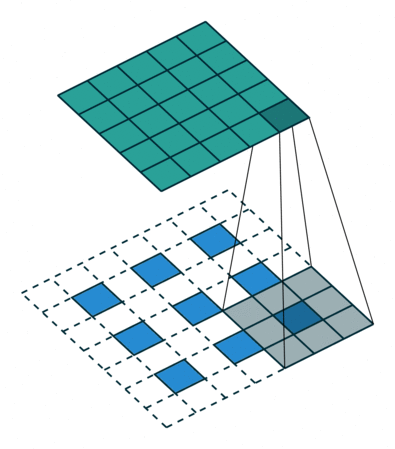
假设反卷积生成的图像中,包含1只黑猫,黑猫身体部分的像素颜色应该是平滑过渡的。或者极端的说,身体部分应该全部都是黑色的。而在实际生成的图像中,该部分却是由深深浅浅的近黑方块组成的,很像棋盘的网络。这就是所谓的棋盘效应。出现的源头就是上采样机制,一般出现在反卷积中。就是在反卷积过程中,当卷积核大小不能被步长整除时,反卷积就会出现重叠问题,插零的时候,输出结果会出现一些数值效应,就像棋盘一样。
参考
棋盘效应(checkerboard artifacts)学习笔记
Deconvolution and Checkerboard Artifacts
PyTorch学习笔记(10)——上采样和PixelShuffle

