这篇论文虽然思想比较简单,但是是第一个将孪生网络用在One-Shot Learning问题上的,所以相当经典,基本上后来的论文都会拿这个论文作比较,所以将这篇文章好好看了看。在此记录一下。
基本信息
- 年份:2015
- 期刊:ICML Deep Learning Workshop. Vol. 2. 2015
- 标签:Metric Learning、Siamese Neural Networks
- 数据:Omniglot
注意该算法个人认为不属于Meta Learning,但是属于Metric Learning
创新点
- 第一个将深度卷积孪生网络用来解决One-Shot Learning问题
- 之前的方案需要特定的先验知识,不具有通用性,而该算法不需要
- 训练好孪生网络以后,不需要经过再训练即可用于One-Shot Learning任务
创新点来源
从One-Shot Learning问题被提出来之后,已有的方法都要使用特定的先验知识或者特定的推理过程,不具有通用性、鲁棒性且算法较为复杂。例如在Omniglot数据集上,之前的方法HBPL就要借助字母的顺序。
所以就想能不能借助神经网络进行自动化的特征提取。神经网络具有很多层的非线性能够捕捉到输入空间中的不变形,而且因为没有利用到先验知识,所以提取出的特征非常powerful。而CNN结构具有局部连接的特性,相当于内嵌了正则化。
至于采用哪个神经网络呢?考虑到这里是One-Shot Learning,每一个新类只有一个有类标的样本,现在有一个未知标签的样本,要将其归类到已知的类别中。最简单的方法的方法是将未知标签的样本和有类标的样本一一进行比较,将最相近的有类标的样本的类标赋值给未知标签的样本,那么就需要有一个网络可以接受两个输入。所以这里就像到了孪生网络。
孪生网络有很多优点:1)因为孪生网络的两个通道采用同一组参数,因此两个很相似的图片输入到网络中不会因为参数不同而映射到不同的特征空间。2)孪生网络具有对称性,因此不管我们按照什么样的顺序输入到网络中,得到的结果都一样,这对于度量学习来说是挺重要的性质。孪生网络的结构如下图所示:
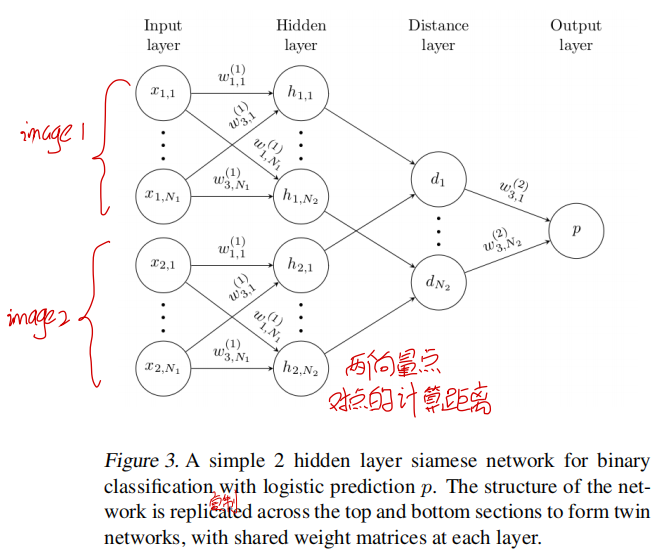
主要过程
这里要注意本文有一个假设前提:网络在训练过程中的验证集上表现良好,那么在One-Shot Learning问题上也表现良好。
数据准备
首先介绍下Omniglot数据集,该数据集中有50个不同的alphabet(字母表),而每一个alphabet(字母表)有从15到40个不等字符(characters),共有1623个字符(characters),每一个字符(characters)均是由20个不同的人(draws)书写出来的。因为Mnist数据集特征为类别少,每类样本多,而该数据类别多,每类样本少,因此又称该数据集为Mnist的镜像数据集。
因为这里是One-Shot Learning,每一个新类只有一个有类标的样本,现在有一个未知标签的样本,要将其归类到已知的类别中。
训练过程:训练集以Pair的形式组成。具体来说从50个alphabet(字母表)选出30个,再从20个draws选出12个用作训练候选集。从训练候选集中随机挑选Pairs。而验证集以One-Shot Learning任务的形式组成,从剩下的10个alphabet(字母表)中挑选One-Shot Learning任务。
测试过程:从保留的10个alphabet(字母表)随机选出一个,从该alphabet(字母表)随机挑选20个字符(characters),在选出2个draws,将第一个draws作为查询集,依次与第二个draws的20类做比较。得到最相近的draws。
网络结构
整体网络结构如下所示。
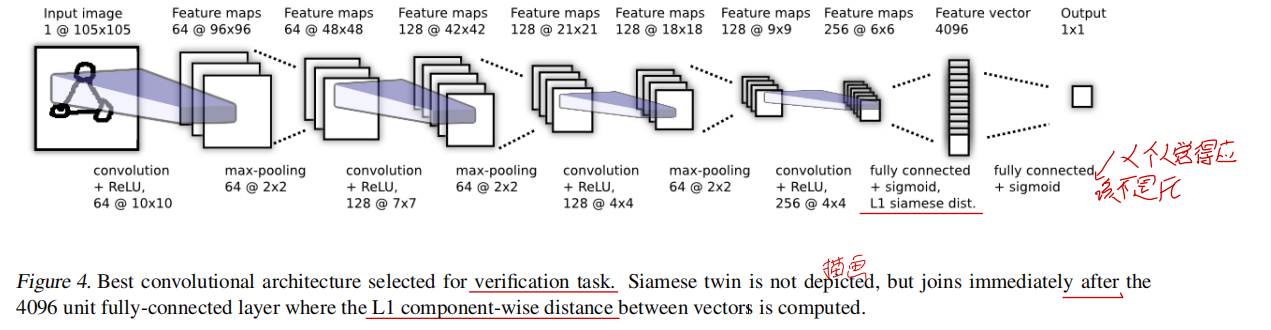
前面的CNN层就不多说了,比较好理解。最重要的是最后两层的理解。最后两层用公式表达如下:
其中$h_{1,L-1}^{(j)}$和$h_{2,L-1}^{(j)}$分别表示孪生网络的第一个流程和第二个流程的第$L-1$层输出的第$j$维。而$h_{1,L-1}$和$h_{2,L-1}$都是前一层的输出经过FC+sigmoid函数得到的。$a_j$是学习到的参数,代表的是距离各个维度的重要性。从这个公式来看,个人觉得网络的最后一层$L$应该不是FC层,而是与$L-1$层的输出点对点相乘的操作。
而在测试阶段,因为采用的是One-Shot Learning任务,查询样本要跟所有的支撑集作比较,最终的类标采用下面的方式得到。
损失函数
损失函数采用的交叉熵损失加正则化手段,公式如下所示。
其中,$i$表示第$i$对样本,$\mathbf{y}\left(x_{1}^{(i)}, x_{2}^{(i)}\right) $为正确类标,当$x_1$和$x_2$属于同类的时候,值为1,否则值为0。
思考
为了保证训练过程中的数据组织形式与测试过程中相同,这里在训练过程中也采用了{支撑集,查询集}这种组合方式。
缺点
- 度量方式采用的为L1范数,无法保证该度量方式完美的适配网络

