基本信息
- 标题:Multi-label Zero-Shot Learning with Structured Knowledge Graphs
- 年份:2018
- 期刊:Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition
- 标签:多标签,零样本,知识图谱
- 数据:NUS-WIDE,COCO
创新点
- 第一个提出用于ML-ZSL的结构信息与知识图谱
- 提出了在语义空间的类别传播算法,使得学到的模型能够泛化到没有见过的类别
- 在标准的multi-label分类任务上,实现了最优性能
创新点来源
人类在识别未知类别时,会根据它与相关已知类别之间的关系,去推理结果。
主要内容
符号和概览
定义${\cal D} = \{ (x_i,y_i) \}_{i=1}^N$为训练样本,其中$x_i \in {\mathbb R}^{d_{feat}}$,$d_{feat}$表示特征的维度,$y^i \in \{0,1\}^{|{ \cal S}|}$为类标,类别集合为${ \cal S}$,$|{ \cal S}|$为可见类别的个数。给定${ \cal S}、{ \cal D}$,multi-label分类任务是学习一个模型,当给出测试实例$\hat x\in {\mathbb R}^{d_{feat}}$时,精准的预测出相应的类别$\hat y\in \{0,1\}^{|{ \cal S}|}$。
对于ML-ZSL任务,有不可见类别集合${\cal U}$,给出一个测试实例$\hat x$时,要预测出属于${ \cal S}、{ \cal U}$的类标,即$\hat y \in \{ 0,1\}^{|{\cal S}|+|{\cal U}|}$,其中${\cal S}$为可见类别集合,${\cal U}$为不可见类别。$|\cdot|$ 符号表示集合的个数。
对于零样本学习,要从已知类别空间中提取语义信息。本文的方法,使用词嵌入(distributed word embeddings)表示类别的语义向量。词嵌入集合可以表示为$W =\{w_v \}_{v=1}^{|{\cal S}|+|{\cal U}|}$,其中$w_v \in {\mathbb R^{d_{emb}}}$表示$|{\cal S}|+|{\cal U}|$中类标$v$的词向量表达,$d_{emb}$表示词嵌入向量的维度。本文使用了Glove产生$W$,$d_{emb}=300$。
本文方法总体图如下所示。知识图谱上的每一个节点(类标)都是有状态的。给定一个输入$\rm x$,经过输入函数${\rm F}_I$,得到$|{\cal S}|$个节点的初始状态$h_v^{(0)}$,接着在知识图谱上进行信息传播更新节点状态。传播算法中,节点$u$(即类标)与节点$v$之间的权重$a_{uv}$使用关系函数${\rm F}_{R}^k$得到。该关系函数的输入为类标特征$w_u$和$w_v$,$k$表示知识图谱中节点$u$与节点$v$关系的种类。上述传播与相互作用经过$T$步之后停止。最后,接一个输出函数${\rm F}_O$产生最终分类概率。

结构化知识图谱
受到Graph Gated Neuron Network的影响,定义有${\cal S}$个节点的图,传播算法使用类似于循环神经网络中的门控循环更新机制。对于ML-ZSL而言,图上的每一个节点$v$对应一个类别。在第$t$步,节点$v$的信念状态向量为$h_{v}^{(t)}\in {\mathbb R}^{d_{hid}}$,这里$d_{hid}=5$。以特征$\rm x$和每一个节点$v$的类别表达$w_v$作为输入,输入函数${\rm F}_I({\rm x},w_v)$计算节点$v$的初始信念状态$h_{v}^{0}$。函数${\rm F}_I$用神经网络实现。
接着使用知识图谱的结构产生传播权重矩阵${\rm A} \in {\mathbb R} ^{|{\cal S}|d_{hid} \times |{\cal S}| d_{hid}}$,每一个元素$a_{uv} \in {\mathbb R} ^{d_{hid} \times d_{hid}}$(怎么来的下面有介绍)。检索每一个节点如$v$的邻接节点,并聚合邻居节点的信念状态信息得到节点$v$的更新量(向量)$u_v^{(t)}$。将$u_v^{(t)}$作为输入,使用GRU网络得到节点$v$更新后信念状态$h_v^{(t)}$。
该过程用表达式表达,即对于节点$v \in {\cal S}$,传播过程如下:
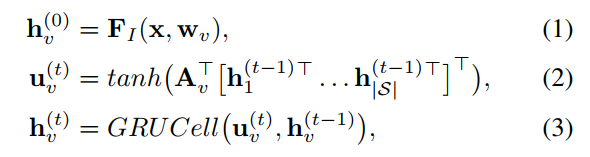
其中,${\rm A}_v \in {\mathbb R} ^{|{\cal S}|d_{hid} \times d_{hid}}$是$\rm A$的子矩阵表示节点$v$的传播权重矩阵(下面会详细介绍)。$|{\cal S}|d_{hid}$表示两者相乘,公式(2)中[]内的维度为$|{\cal S}| \times d_{hid}$,${\rm A}_v^T$的维度为$d_{hid} \times |{\cal S}|d_{hid}$,所以括号内相乘后的维度为$d_{hid} \times 1$。
GRUCell的表达式如下:
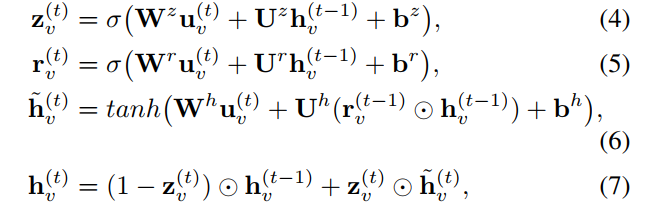
其中,$\rm W、U、b$是待学习的参数。
对于每一步$t$,使用输出函数${\rm F}_O$得到每一个类标节点的置信度。
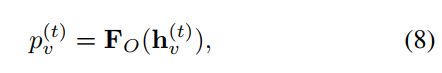
传播矩阵的学习
在公式(2)中可以看出,节点$v$的更新量(向量)$u_v^{(t)}$是${\rm A}_v$中其他节点信念状态的加权组合。将${\rm A}_v$中,与节点$v$不相邻的节点位置置为0,相邻的位置为非零权重。这样节点$v$只会从与它相邻的节点信念状态中得到信息。
给定$\varepsilon$中的一条边,其类型为$k$,传播权重$a_{uv} \in {\mathbb R} ^{d_{hid} \times d_{hid}}$由下式得出:
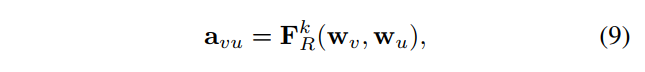
其中,$w_v$和$w_u$表示类别节点$v$和$u$的词向量。传播矩阵的学习机制如下图所示。第$i$列表示第$i$个节点与其它节点之间的权重。节点$j$与$i$相邻且关系是正的,则输入$w_i、w_j$到函数${\rm F}_R^{pos}$中,得到两者的连接权重。相反的,节点$k$与$i$相邻但关系是负的,则输入$w_i、w_k$到函数${\rm F}_R^{neg}$中,得到两者的连接权重。另外需要注意的是,矩阵$\rm A$是对称的。

从这可以看出,对于每一个边类型$k$,${\rm F}_{R}^{k}$学习从词向量空间到权重矩阵的映射。更重要的是,学习从语义空间的映射,允许我们将上述模型泛化到不可见类别中。
从ML到ML-ZSL
模型损失函数使用每一个类别节点的BCE加权求和。在每一time step的网络${\rm F}_O$ 的输出后,损失$\cal L$定义为:
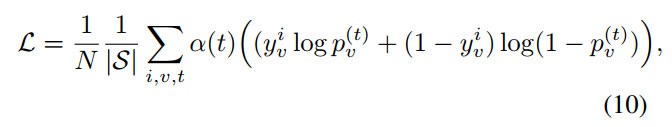
其中,$N$表示训练样本总数,$|\cal S|$表示已知类别的个数,$i$表示第$i$个样本,$v$表示第$v$个节点(即第$v$类),$t$表示更新的步数。若第$i$个样本属于第$v$类,则$y_v^i=1$,否则$y_v^i=0$。个人感觉上面的$p_v^{(t)}$应该是$p_v^{(i,t)}$,即第$i$个样本在第t步预测出属于第$v$类的概率。权重$\alpha (t)=1/(T-t+1)$使得随着$t$的增加(分母减小,整体增大),预测的更加精准。在ML预测阶段,时间$T$的输出$p_v^{(T)}$被用来预测输出。
然而,对于ML-ZSL预测,是有点不同的。我们扩展$\rm A$到$\hat {\rm A} \in {\mathbb R}^{(|{\cal S}| + |\cal U|)d_{hid} \times (|{\cal S}| + |\cal U|)d_{hid}}$,所以它能够编码结构知识图谱中不可见类别的关系。我们也限制$\hat {\rm A}$(即限制边),使得传播只能从已知类到未知类。更新量$u_v^{(t)}$由来自$\cal S$和$\cal U$的邻接节点计算得到。然后更改(2)式为:

该模型能够使用${\rm F}_I$计算不可见类别的初始信念状态,然后执行从可见类到不可见类的传播(也有不可见类别之间的传播)。最后,对于每一个不可见类别的预测输出由${\rm F}_O$得到。ML-ZSL的传播机制如下图所示($\hat {\rm A}$究竟是怎么限制的)。
实验
建立知识图谱
这里使用WordNet建立知识图谱。为知识图谱建立三种类别关系,super-subordinate, positive correlation, and negative correlation ,其中super-subordinate也称为hyponymy, hypernomy, or ISA relation,能够直接从WordNet中得到。对于positive correlation, and negative correlation ,使用WUP similarity(定义在WordNet中)并经过相似度阈值得到。对于位于positive and negative thresholds之间的类别对,视为它们之间没有任何直接关系。
此外,如果一对类别显示出super-subordinate,我们将直接在图中应用依赖关系,而不进一步计算它的positive correlation, and negative correlation。
接下来的实验中,均固定$T=5$。
数据集
这里使用多类别数据集NUS-WIDE和COCO。
NUS-WIDE有269648张图片,记NUS-1000为1000类的划分方式,NUS-81为81类的划分方式。排除掉没有任何类别的图片,总共有90360张图片。我们将数据集划分为75000训练样本,5000个验证图片,10360个测试图片。
COCO数据集有80类,78081张图片用于训练,4000张图片用于验证集,40137张图片作为测试。
这两种数据集,均输入图片到ResNet-152中提取2048维向量作为上面提到的输入$\rm x$。
Multi-Label分类
多分类结果如下,其中P表示准确率,R表示召回率。
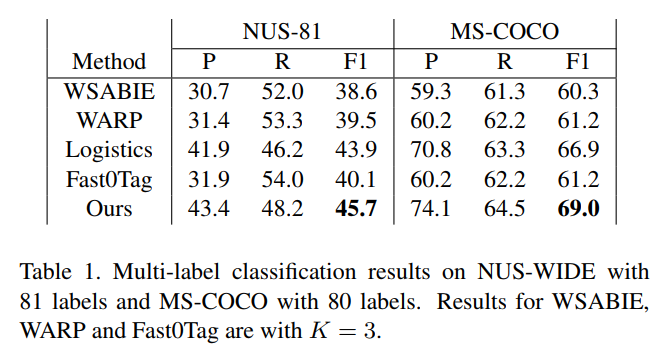
准确率(Precision):P=TP/(TP+FP)。通俗地讲,就是预测正确的正例数据占预测为正例数据的比例。
召回率(Recall):R=TP/(TP+FN)。通俗地讲,就是预测为正例的数据占实际为正例数据的比例
F1:$F1=\frac{2}{\frac{1}{P} + \frac{1}{R}}$。F1的值同时受到P、R的影响。
ML-ZSL
将NUS-81中的类别作为不可见类别$\cal U$,将NUS-1000移除75个重复类别(为什么是75个?)后的925个类别作为已知类别$\cal S$。结果如下所示:
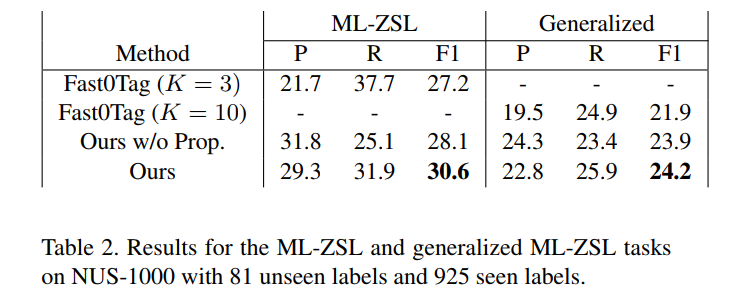
其中,Ours w/o Prop. 表示$T=0$时的结果。Generalized表示只在可见类别上建模,但是要在测试过程中,对可见类和不可见类进行同时进行预测。
传播机制的分析
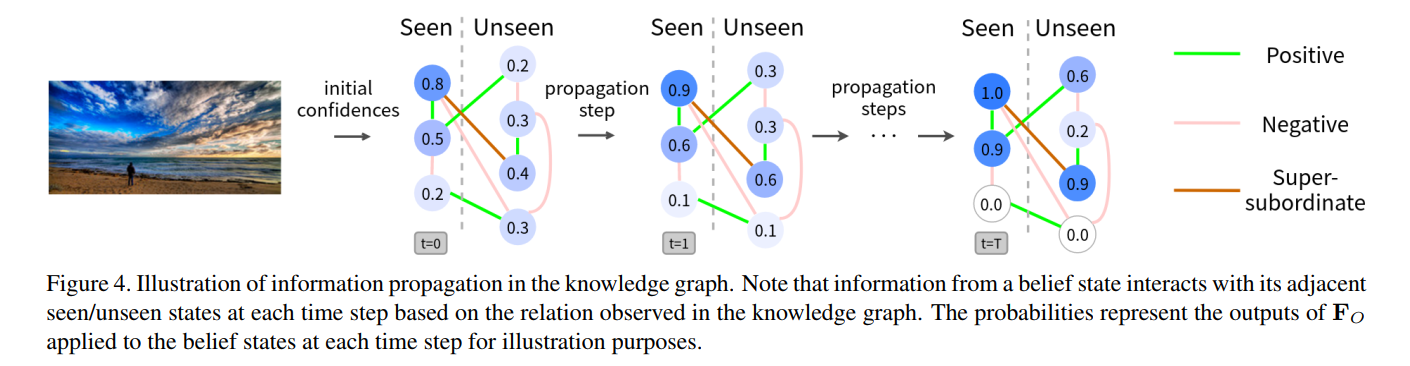
对传播机制进行可视化,如下图所示。将几个类别从$t=0$到$t=5$的预测概率进行可视化。对应的知识图谱子图也在图中给出。从结果可以看出,前几个传播过程对预测结果影响最大。
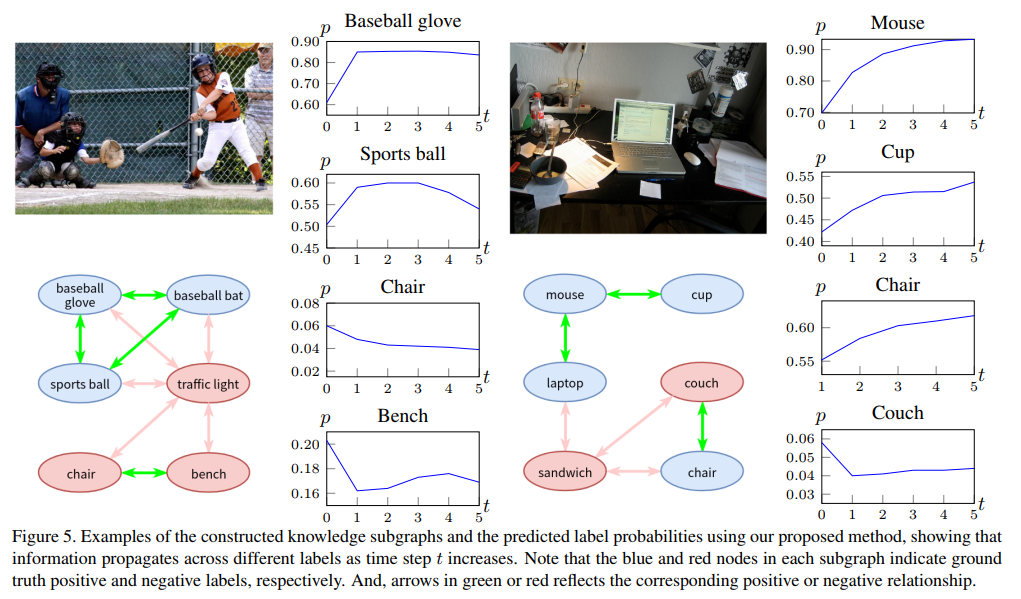
将NUS-81和COCO在不同$t$下的性能可视化如下,也可以得到相同的结论。
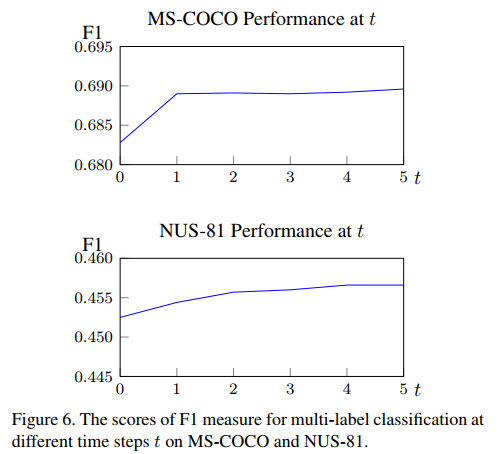
在使用NUS-WIDE 1000数据集进行generalized ML-ZSL实验是,也可以观察到相同的趋势。

启发
- 知道拓扑结构后,可以使用不同的边类型,定义不同的权重求法
缺点
- 论文细节介绍的不是很清楚,好多函数怎么构造的,网络的详细结构都没介绍
- 未知类别的名称要事先得知
- 也需要知道拓扑结构

