开新坑了,最近在攻击语音合成系统,现在学习一下语音基础知识。
辅音和元音的区别
- 辅音发音时,气流在通过咽头、口腔的过程中, 要受到某部位的阻碍;元音发音时,气流在咽头、 口腔不受阻碍。这是元音和辅音最主要的区别。
- 辅音发音时,发音器官成阻的部位特别紧张; 元音发音时发音器官各部位保持均衡的紧张状态。
- 辅音发音时,气流较强;元音发音时,气流较 弱。
- 辅音发音时,声带不一定振动,声音一般不响亮;元音发音时,声带振动,声音比辅音响亮。
一般只有元音(一些介于元音辅音中间分类不明的音暂不讨论)才会有共振峰,而元音的音质由声道的形状决定,而声道的形状又通过发音的动作来塑造(articulatory+movements)。
清音和浊音
- 清音:声带不振动
- 浊音:声带振动而发音
- 元音都是浊音、辅音有清音也有浊音。
波形、频谱和语谱(声谱)
以下内容主要来源于不同元音辅音在声音频谱的表现是什么样子? - 王赟 Maigo的回答 - 知乎。
波形
声音最直接的表示方式是波形,英文叫waveform。另外两种表示方式(频谱和语谱图)下文再说。波形的横轴是时间(所以波形也叫声音的时域表示),纵轴的含义并不重要,可以理解成位移(声带或者耳机膜的位置)或者压强。
当横轴的分辨率不高的时候,语音的波形看起来就是像你贴的图中一样,呈现一个个的三角形。这些三角形的轮廓叫作波形的包络(envelope)。包络的大小代表了声音的响度。一般来说,每一个音节会对应着一个三角形,因为一般地每个音节含有一个元音,而元音比辅音听起来响亮。但例外也是有的,比如:1) 像/s/这样的音,持续时间比较长,也会形成一个三角形;2) 爆破音(尤其是送气爆破音,如/p/)可能会在瞬时聚集大量能量,在波形的包络上就体现为一个脉冲。
下面这张图中上方的子图,是读单词pass /pæs/的录音。它的横坐标已经被拉开了一些,但其实这个波形是由两个“三角形”组成的。0.05秒处那个小突起是爆破音/p/,0.05秒到0.3秒是元音/æ/,0.3到0.58秒是辅音/s/。

如果你把横轴的分辨率调高,比如只观察0.02s秒甚至更短时间内的波形,你就可以看到波形的精细结构(fine structure),像上图的下面两个子图。波形的精细结构可能呈现两种情况:一种是有周期性的,比如左边那段波形(图中显示了两个周期多一点),这种波形一般是元音或者辅音中的鼻音、浊擦音以及/l/、/r/等;另一种是乱的,比如右边那段波形,这种波形一般是辅音中的清擦音。辅音中的爆破音,则往往表现为一小段静音加一个脉冲(如pass开头的/p/)。
频谱
看完了声音的时域表示,我们再来看它的频域表示——频谱(spectrum)。它是由一小段波形做傅里叶变换(Fourier transform)之后取模得到的。注意,必须是一小段波形,太长了弄出来的东西(比如你贴的右边的图)就没意义了!这样的一小段波形(通常在0.02~0.05s这样的数量级)称为一帧(frame)。下面是读的pass的波形中,以0.17s和0.4s为中心截取0.04s波形经傅里叶变换得到的频谱。频谱的横轴是频率;录音的采样率用的是16000 Hz,频谱的频率范围也是0 ~ 16000 Hz。但由于0 ~ 8000 Hz和8000 ~ 16000 Hz的频谱是对称的,所以一般只画0 ~ 8000 Hz的部分。
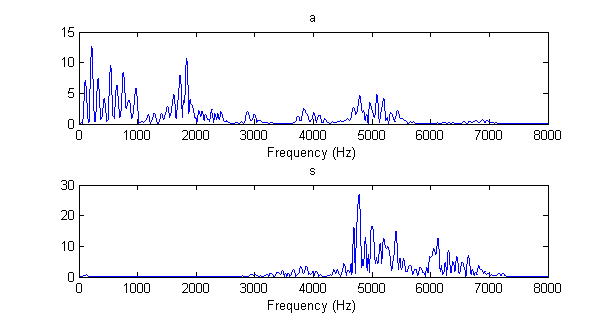
频谱跟波形一样,也有包络和精细结构。你把横轴压缩,看到的就是包络;把横轴拉开,看到的就是精细结构。我上面这两张图使得二者都能看到。
第一个频谱是元音/æ/的频谱,可以看到它的精细结构是有周期性的,每隔108 Hz出现一个峰。从这儿也可以看出来,语音不是一个单独的频率,而是由许多频率的简谐振动叠加而成的。第一个峰叫基音,其余的峰叫泛音。第一个峰的频率(也是相邻峰的间隔)叫作基频(fundamental frequency),也叫音高(pitch),常记作$f_0$。有时说“一个音的频率”,就是特指基频。基频的倒数叫基音周期。你再看看上面元音/æ/的波形的周期,大约是0.009 s,跟基频108 Hz吻合。频谱上每个峰的高度是不一样的,这些峰的高度之比决定了音色(timbre)。不过对于语音来说,一般没有必要精确地描写每个峰的高度,而是用“共振峰”(formant)来描述音色。共振峰指的是包络的峰。在我这个图中,忽略精细结构,可以看到0~1000 Hz形成一个比较宽的峰,1800 Hz附近形成一个比较窄的峰。共振峰的频率一般用$f_1$、$f_2$等等来表示。上图中,$f_1$是多少很难精确地读出来,但$f_2 \approx 1800Hz$。当然,在2800 Hz、3800 Hz、5000 Hz处还有第三、四、五共振峰,但它们与第一、二共振峰相比就弱了许多。除了元音以外,辅音中的鼻音、浊擦音以及/l/、/r/等也具有这种频谱,可以讨论基频和共振峰频率(不过浊擦音一般不讨论共振峰频率)。
第二个频谱是辅音/s/的频谱。可以看出它的精细结构是没有周期性的,所以就无所谓基频。一般也不提这种频谱的共振峰。清擦音的频谱一般都是这样。
语谱(声谱)
我们最后来看一下声音的第三种表示方式——语谱图(spectrogram)。上面说过,频谱只能表示一小段声音。那么,如果我想观察一整段语音信号的频域特性,要怎么办呢?我们可以把一整段语音信号截成许多帧,把它们各自的频谱“竖”起来(即用纵轴表示频率),用颜色的深浅来代替频谱强度,再把所有帧的频谱横向并排起来(即用横轴表示时间),就得到了语谱图,它可以称为声音的时频域表示。下面我就偷懒,不用Matlab自己画语谱图,而用Cool Edit绘制上面“pass”的语谱图,如下:
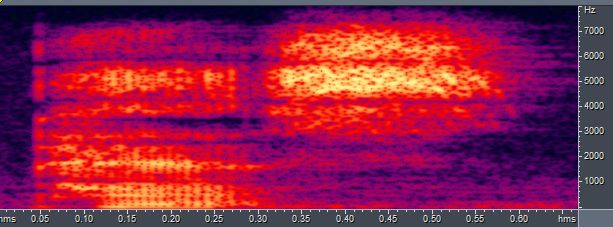
注意横轴是时间,纵轴是频率,颜色越亮代表强度越大。可以观察一下0.17s和0.4s处,是不是跟我上面画的频谱相似?然后再试着从这张语谱图上读出元音/æ/的第二共振峰频率。
语谱图的好处是可以直观地看出共振峰频率的变化。我上面读的“pass”中只有一个单元音,如果有双元音就会非常明显了。比如下面这张我读的“eye” /aɪ/,可以非常明显地看出在元音从/a/向/ɪ/过渡的阶段(0.2 ~ 0.25s),$f_1$在降低,而$f_2$在升高。
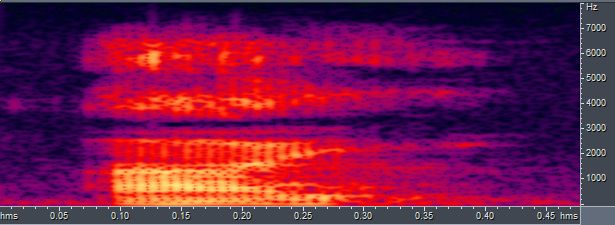
元音与共振峰的关系已经研究得比较透彻了,简单地说:
1) 开口度越大, $ f_{1} $ 越高;
2) 舌位越靠前, $ f_{2} $ 越高;
3) 不圆唇元音的 $ f_{3} $ 比圆唇元音高。例如, $ / \mathrm{a} / $ 是开、后、不圆唇元音, 所以 $ f_{1} $ 高, $ f_{2} $ 低, $ f_{3} $ 高;/y/(即汉语拼音的ü)是闭、前、圆 唇元音, 所以 $ f_{1} $ 低, $ f_{2} $ 高, $ f_{3} $ 低。也许大家见过下图那样的元音图Q (vowel chart) , 我把 $ f_{1} $ 和 $ f_{2} $ 的变化方向标 $ Q $ 上去。

$f_3$最明显的体现其实是在英语的辅音/r/中,例如下面我读的erase /ɪ’reɪz/的语谱图,可以看到辅音/r/处(0.19s左右)$f_3$明显低,把$f_2$也压下去了。
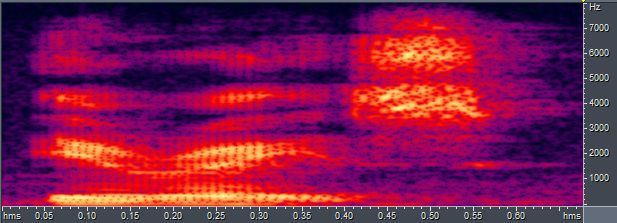
清擦音可以根据能量集中的频段来分辨。下面是我读的/f/, /θ/, /s/, /ʃ/的语谱图。浊擦音会在清擦音的基础上有周期性的精细结构。
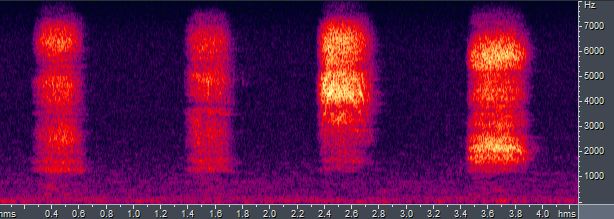
爆破音的爆破时间很短,在语谱图上一般较难分辨。
“两个音之间的音是什么样子”,就要分情况讨论了。
1) 如果是两个元音,那么可以在元音图上找到两个元音,取它们连线的中点。这对应着把$f_1$、$f_2$分别取平均。
2) 如果是两个清擦音,那么可以把它们的频谱取平均,这样听起来应该是个四不像(后来我做了实验,结果见这里:Mixture of Unvoiced Fricatives)。
3) /t/和/ʃ/属于不同类型的辅音,很难定义它们“之间”是什么东西。
总结
语音基本概念
以下内容主要来源于语音基础知识(附相关实现代码)。在不理解的地方我会加上自己的注释。
声波通过空气传播,被麦克风接收,通过采样、量化、编码转换为离散的数字信号,即波形文件。音量、音高和音色是声音的基本属性。
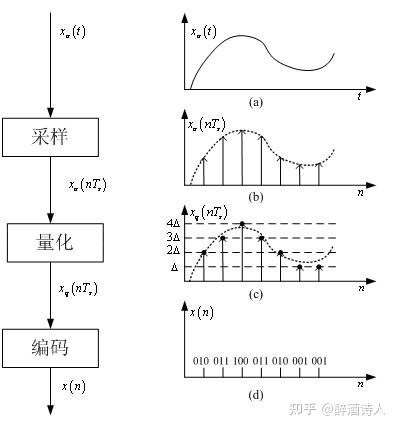
1)采样:原始的语音信号是连续的模拟信号,需要对语音进行采样,转化为时间轴上离散的数据。
采样后,模拟信号被等间隔地取样,这时信号在时间上就不再连续了,但在幅度上还是连续的。经过采样处理之后,模拟信号变成了离散时间信号。
采样频率是指一秒钟内对声音信号的采样次数,采样频率越高声音的还原就越真实越自然。
在当今的主流采集卡上,采样频率一般共分为 22.05KHz、44.1KHz、48KHz 三个等级,22.05KHz 只能达到 FM 广播的声音品质,44.1KHz 则是理论上的 CD 音质界限(人耳一般可以感觉到 20-20K Hz 的声音,根据香农采样定理,采样频率应该不小于最高频率的两倍,所以 40KHz 是能够将人耳听见的声音进行很好的还原的一个数值,于是 CD 公司把采样率定为 44.1KHz),48KHz 则更加精确一些。
对于高于 48KHz 的采样频率人耳已无法辨别出来了,所以在电脑上没有多少使用价值。
2)量化:进行分级量化,将信号采样的幅度划分成几个区段,把落在某区段的采样到的样品值归成一类,并给出相应的量化值。根据量化间隔是否均匀划分,又分为均匀量化和非均匀量化。
均匀量化的特点为 “大信号的信噪比大,小信号的信噪比小”。缺点为 “为了保证信噪比要求,编码位数必须足够大,但是这样导致了信道利用率低,如果减少编码位数又不能满足信噪比的要求”(根据信噪比公式,编码位数越大,信噪比越大,通信质量越好)。
通常对语音信号采用非均匀量化,基本方法是对大信号使用大的量化间隔,对小信号使用小的量化间隔。由于小信号时量化间隔变小,其相应的量化噪声功率也减小(根据量化噪声功率公式),从而使小信号时的量化信噪比增大,改善了小信号时的信噪比。
量化后,信号不仅在时间上不再连续,在幅度上也不连续了。经过量化处理之后,离散时间信号变成了数字信号。
3)编码:在量化之后信号已经变成了数字信号,需要将数字信号编码成二进制。“CD 质量” 的语音采用 44100 个样本每秒的采样率,每个样本 16 比特,这个 16 比特就是编码的位数。
采样,量化,编码的过程称为 A/D(从模拟信号到数字信号)转换,如上图 1 所示。
补充比特率的概念:比特率是指每秒传送的比特(bit)数。单位为 bps(Bit Per Second),比特率越高,传送的数据越大,音质越好。以电话为例,每秒3000点取样,每个样本是7比特,那么电话的比特率是21000。而CD是每秒44100点取样,两个声道,每个取样是13位PCM编码,所以CD的比特率是$44100213=1146600$,也就是说CD每秒的数据量大约是144KB,而一张CD的容量是74分等于4440秒,就是639360KB=640MB。
能量
音频的能量通常指的是时域上每帧的能量,幅度的平方。在简单的语音活动检测(Voice Activity Detection,VAD)中,直接利用能量特征:能量大的音频片段是语音,能量小的音频片段是非语音(包括噪音、静音段等)。这种 VAD 的局限性比较大,正确率也不高,对噪音非常敏感。
1 | def __init__(self, input_file, sr=None, frame_len=512, n_fft=None, win_step=2 / 3, window="hamming"): |
短时能量
短时能量体现的是信号在不同时刻的强弱程度。设第 n 帧语音信号的短时能量用$E_n$表示,则其计算公式为:
上式中,M 为帧长,$x_n(m)$为该帧中的样本点。
1 | def short_time_energy(self): |
声强和声强级(声压和声压级)
单位时间内通过垂直于声波传播方向的单位面积的平均声能,称作声强,声强用 P 表示,单位为 “瓦 / 平米”。实验研究表明,人对声音的强弱感觉并不是与声强成正比,而是与其对数成正比,所以一般声强用声强级来表示:
其中,P 为声强, $P’=10e^{-12}$单位($w/m^2$)称为基本声强,声强级的常用单位是分贝 (dB)。
1 | def intensity(self): |
过零率
过零率体现的是信号过零点的次数,体现的是频率特性。
其中,N 表示帧数,M 表示每一帧中的样本点个数,sgn 为符号函数,即:
1 | def zero_crossing_rate(self): |
基频和基音周期
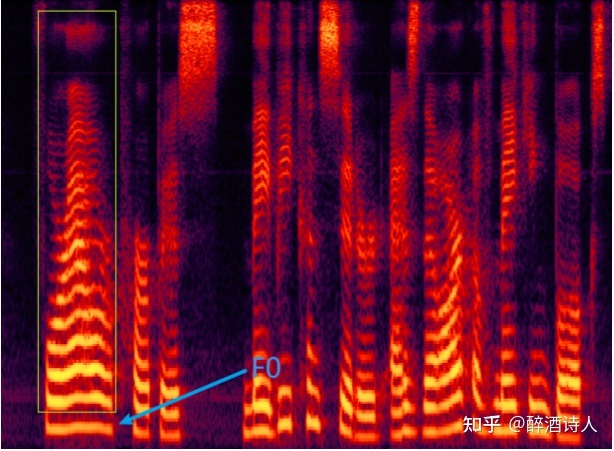
基音周期反映了声门相邻两次开闭之间的时间间隔,基频(fundamental frequency, F0)则是基音周期的倒数,对应着声带振动的频率,代表声音的音高,声带振动越快,基频越高。如图 2 所示,蓝色箭头指向的就是基频的位置,决定音高。它是语音激励源的一个重要特征,比如可以通过基频区分性别。一般来说,成年男性基频在 100-250Hz 左右,成年女性基频在 150-350Hz 左右,女声的音高一般比男声稍高。 人类可感知声音的频率大致在 20-20000Hz 之间,人类对于基频的感知遵循对数律,也就是说,人们会感觉 100Hz 到 200Hz 的差距,与 200Hz 到 400Hz 的差距相同。因此,音高常常用基频的对数来表示。
这部分的详细介绍可以看前面的
波形、频谱和语谱(声谱)小节。
音高
音高(pitch)是由声音的基频决定的,音高和基频常常混用。可以这样认为,音高(pitch)是稀疏离散化的基频(F0)。由规律振动产生的声音一般都会有基频,比如语音中的元音和浊辅音;也有些声音没有基频,比如人类通过口腔挤压气流的清辅音。在汉语中,元音有 a/e/i/o/u,浊辅音有 y/w/v,其余音素比如 b/p/q/x 等均为清辅音,在发音时,可以通过触摸喉咙感受和判断发音所属音素的种类。
1 | def pitch(self, ts_mag=0.25): |
共振峰
声门处的准周期激励进入声道时会引起共振特性,产生一组共振频率,这一组共振频率称为共振峰频率或简称共振峰。共振峰包含在语音的频谱包络中,频谱极大值就是共振峰。频率最低的共振峰称为第一共振峰,对应的频率也称作基频,决定语音的 F0,其它的共振峰统称为谐波,如上图 2 所示,蓝色箭头指向频谱的第一共振峰,也就是基频的位置,决定音高;而绿框则是其它共振峰,统称为谐波。谐波是基频对应的整数次频率成分,由声带发声带动空气共振形成的,对应着声音三要素的音色。谐波的位置,相邻的距离共同形成了音色特征。谐波之间距离近听起来则偏厚粗,之间距离远听起来偏清澈。在男声变女声的时候,除了基频的移动,还需要调整谐波间的包络,距离等,否则将会丢失音色信息。
汇总
为了有一个直观的图来解释上述的理论,可以把语音波形、短时能量、声强级、过零率、音高绘制在一张图上,如下图 3 所示:
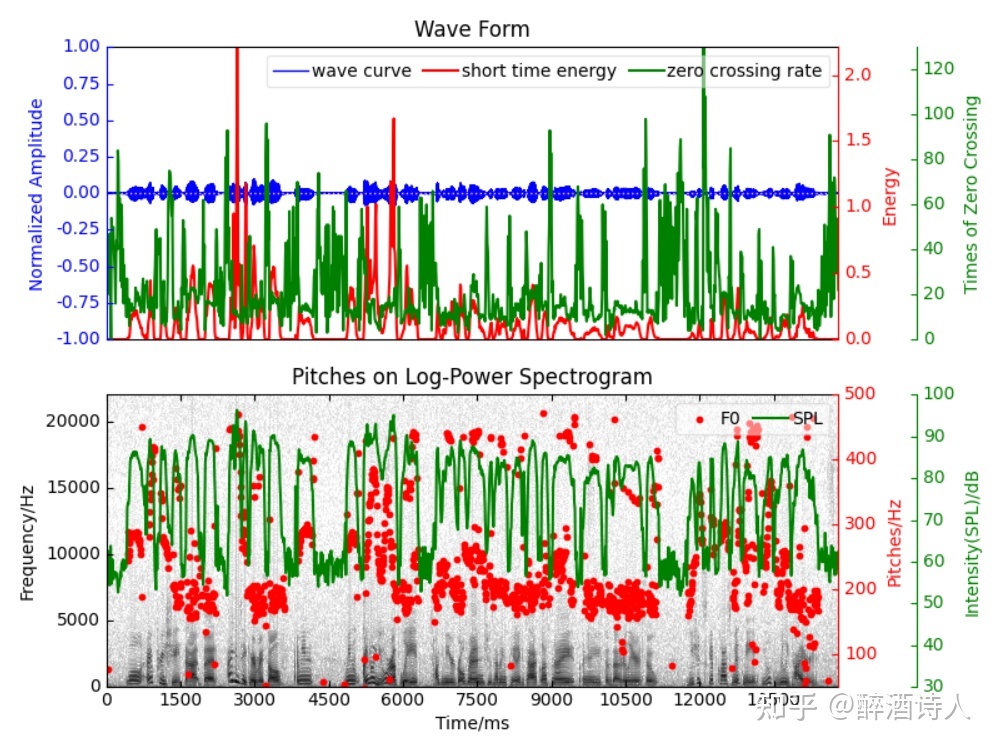
语音信号的预处理操作
以下内容主要来源于语音基础知识(附相关实现代码)。在不理解的地方我会加上自己的注释。
在进行语音特征(如 MFCC、频谱图、声谱图等)提取之前一般要进行语音信号的预处理操作,主要包括:预加重、分帧、加窗。
预加重
语音经过说话人的口唇辐射发出,受到唇端辐射抑制,高频能量明显降低。一般来说,当语音信号的频率提高两倍时,其功率谱的幅度下降约 6dB,即语音信号的高频部分受到的抑制影响较大。比如像元音等一些因素的发音包含了较多的高频信号的成分,高频信号的丢失,可能会导致音素的共振峰并不明显,使得声学模型对这些音素的建模能力不强。预加重(pre-emphasis)是个一阶高通滤波器,可以提高信号高频部分的能量,给定时域输入信号$x[n]$,预加重之后信号为:
其中,a 是预加重系数,一般取 0.97 或 0.95。如下图 4 所示,元音音素 /aa/ 原始的频谱图(左)和经过预加重之后的频谱图(右)。
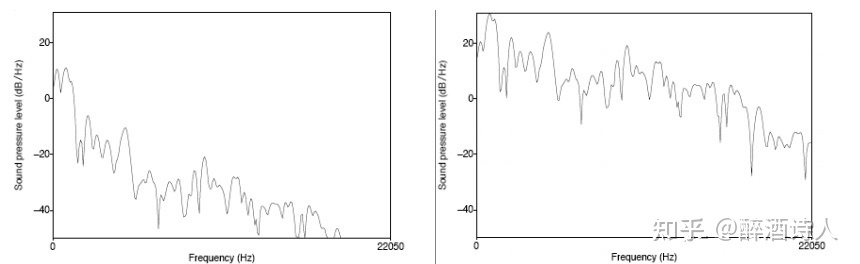
1 | def preemphasis(y, coef=0.97, zi=None, return_zf=False): |
分帧
语音信号是非平稳信号,考虑到发浊音时声带有规律振动,即基音频率在短时范围内时相对固定的,因此可以认为语音信号具有短时平稳特性,一般认为 10ms~50ms 的语音信号片段是一个准稳态过程。_短时分析_采用分帧方式,一般每帧帧长为 20ms 或 50ms。假设语音采样率为 16kHz,帧长为 20ms,则一帧有 16000×0.02=320 个样本点。
相邻两帧之间的基音有可能发生变化,如两个音节之间,或者声母向韵母过渡。为确保声学特征参数的平滑性,一般采用重叠取帧的方式,即相邻帧之间存在重叠部分。一般来说,帧长和帧移的比例为 1:4 或 1:5。
短时分析:虽然语音信号具有时变特性,但是在一个短时间范围内(一般认为在 10-30ms)其特性基本保持相对稳定,即语音具有短时平稳性。所以任何语音信号的分析和处理必须建立在 “短时” 的基础上,即进行“短时分析”。
1 | def framesig(sig,frame_len,frame_step): |
加窗
分帧相当于对语音信号加矩形窗(用矩形窗其实就是不加窗),矩形窗在时域上对信号进行截断,在边界处存在多个旁瓣,会发生频谱泄露。为了减少频谱泄露,通常对分帧之后的信号进行其它形式的加窗操作。常用的窗函数有:汉明(Hamming)窗、汉宁(Hanning)窗和布莱克曼(Blackman)窗等。 加窗主要是为了使时域信号似乎更好地满足 FFT 处理的周期性要求,减少泄漏(加窗不能消除泄漏,只能减少, 如下图 5 所示)。
什么是频谱泄露?
音频处理中,经常需要利用傅里叶变换将时域信号转换到频域,而一次快速傅里叶变换(FFT)只能处理有限长的时域信号,但语音信号通常是长的,所以需要将原始语音截断成一帧一帧长度的数据块。这个过程叫信号截断,也叫分帧。分完帧后再对每帧做 FFT,得到对应的频域信号。FFT 是离散傅里叶变换(DFT)的快速计算方式,而做 DFT 有一个先验条件:分帧得到的数据块必须是整数周期的信号,也即是每次截断得到的信号要求是周期主值序列。但做分帧时,很难满足周期截断,因此就会导致频谱泄露。一句话,频谱泄露就是分析结果中,出现了本来没有的频率分量。比如说,50Hz 的纯正弦波,本来只有一种频率分量,分析结果却包含了与 50Hz 频率相近的其它频率分量。
非周期的无限长序列,任意截取一段有限长的序列,都不能代表实际信号,分析结果当然与实际信号不一致!也就是会造成频谱泄露。而周期的无限长序列,假设截取的是正好一个或整数个信号周期的序列,这个有限长序列就可以代表原无限长序列,如果分析的方法得当的话,分析结果应该与实际信号一致!因此也就不会造成频谱泄露。
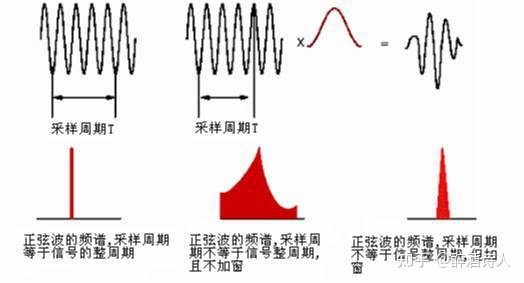
汉明窗的窗函数为: $ W_{\mathrm{ham}}[n]=0.54-0.46 \cos \left(\frac{2 \pi n}{N}-1\right) $;汉宁窗的窗函数为: $ W_{h a n}[n]=0.5\left[1-\cos \left(\frac{2 \pi n}{N}-1\right)\right] $ ,其中$n$介于0到$ \mathrm{N}-1 $ 之间,$ \mathrm{N} $ 是窗的长度。
加窗就是用一定的窗函数$ w(n) $来乘$ s(n) $, 从而形成加窗语音信号$s_{w}(n)=\mathrm{s}(\mathrm{n}) * w(\mathrm{n}) $。
1 | def framesig(sig,frame_len,frame_step,winfunc=lambda x:numpy.ones((x,))): |
语音声学特征介绍
以下内容主要来源于论文笔记:语音情感识别(四)语音特征之声谱图,log梅尔谱,MFCC,deltas
声音信号本是一维的时域信号,直观上很难看出频率变化规律。傅里叶变换可把它变到频域上,虽然可看出信号的频率分布,但是丢失了时域信息,无法看出频率分布随时间的变化。为了解决这个问题,很多时频分析手段应运而生,如短时傅里叶,小波,Wigner分布等都是常用的时频域分析方法。
原始信号
从音频文件中读取出来的原始语音信号通常称为 raw waveform,是一个一维数组,长度是由音频长度和采样率决定,比如采样率 Fs 为 16KHz,表示一秒钟内采样 16000 个点,这个时候如果音频长度是 10 秒,那么 raw waveform 中就有 160000 个值,值的大小通常表示的是振幅。
(线性)声谱图
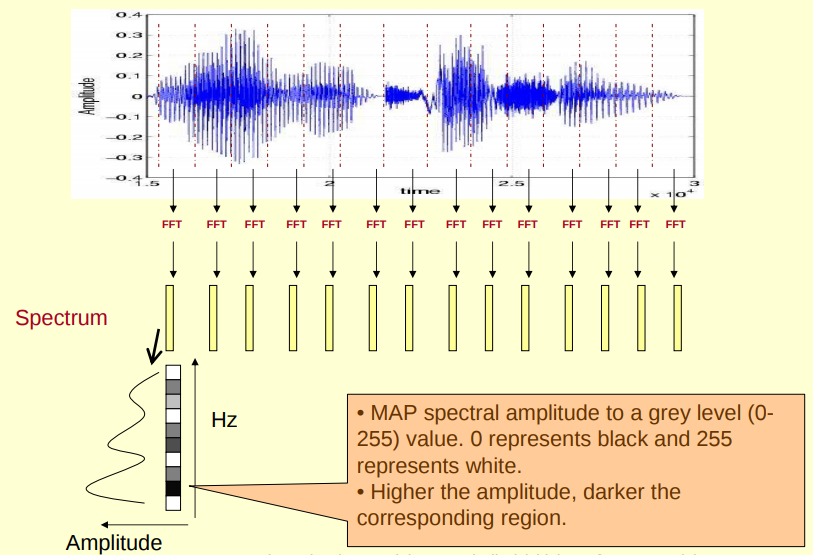
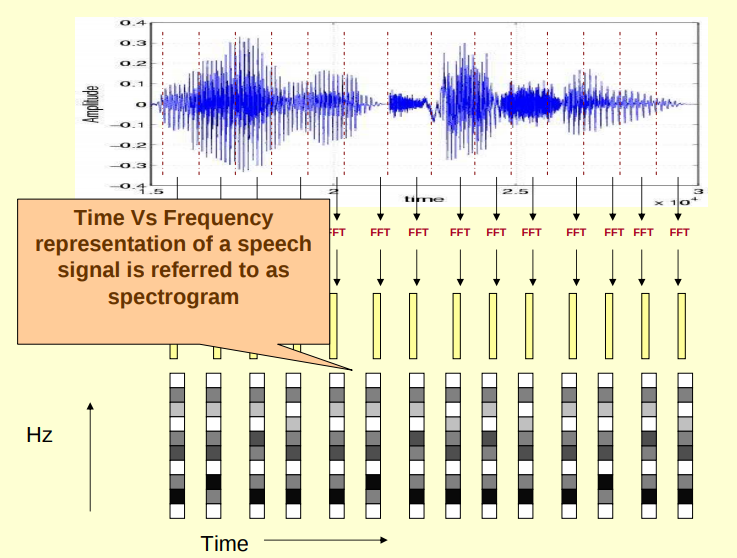
(1)对原始信号进行分帧加窗后,可以得到很多帧,对每一帧做 FFT(快速傅里叶变换),傅里叶变换的作用是把时域信号转为频域信号,把每一帧 FFT 后的频域信号(频谱图)在时间上堆叠起来就可以得到声谱图,其直观理解可以形象地表示为以下几个图,图源见CMU 语音课程 slides。
(2)有些论文提到的 DCT(离散傅里叶变换)和 STFT(短时傅里叶变换)其实是差不多的东西。STFT 就是对一系列加窗数据做 FFT。而 DCT 跟 FFT 的关系就是:FFT 是实现 DCT 的一种快速算法。
(3)FFT 有个参数 N,表示对多少个点做 FFT,如果一帧里面的点的个数小于 N 就会 zero-padding 到 N 的长度。对一帧信号做 FFT 后会得到 N 点的复数,这个点的模值就是该频率值下的幅度特性。每个点对应一个频率点,某一点 n(n 从 1 开始)表示的频率为$F_n = (n-1)*Fs/N$,第一个点(n=1,Fn 等于 0)表示直流信号,最后一个点 N 的下一个点(n=N+1,Fn=Fs 时,实际上这个点是不存在的)表示采样频率 Fs。
(4)FFT 后我们可以得到 N 个频点,频率间隔(也叫频率分辨率或)为 Fs / N,比如,采样频率为 16000,N 为 1600,那么 FFT 后就会得到 1600 个点,频率间隔为 10Hz,FFT 得到的 1600 个值的模可以表示 1600 个频点对应的振幅。因为 FFT 具有对称性,当 N 为偶数时取 N/2+1 个点,当 N 为奇数时,取 (N+1)/2 个点,比如 N 为 512 时最后会得到 257 个值。
(5)用 python_speech_feature 库时可以看到有三种声谱图,包括振幅谱,功率谱(有些资料称为能量谱,是一个意思,功率就是单位时间的能量),log 功率谱。振幅谱就是 fft 后取绝对值。功率谱就是在振幅谱的基础上平方然后除以 N。log 功率谱就是在功率谱的基础上取 10 倍 lg,然后减去最大值。得到声谱图矩阵后可以通过 matplotlib 来画图。
(6)常用的声谱图都是 STFT 得到的,另外也有用 CQT(constant-Q transform)得到的,为了区分,将它们分别称为 STFT 声谱图和 CQT 声谱图。

梅尔声谱图
梅尔频谱的英文为Mel-spectrogram。
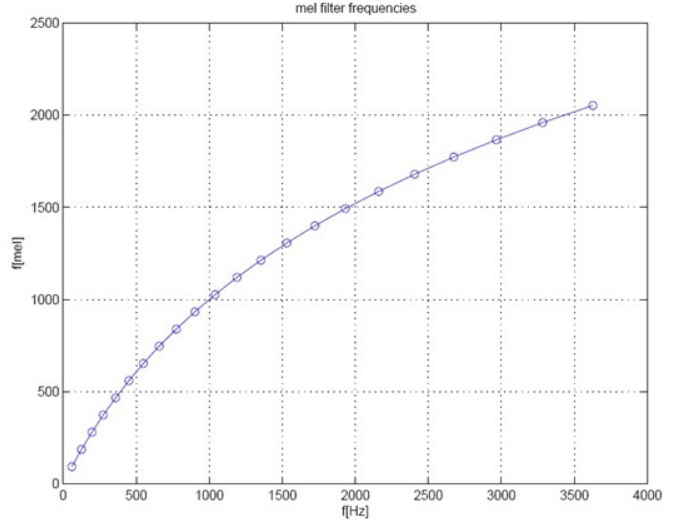
(1)人耳听到的声音高低和实际(Hz)频率不呈线性关系,用 Mel 频率更符合人耳的听觉特性(这正是用 Mel 声谱图的一个动机,由人耳听力系统启发),即在 1000Hz 以下呈线性分布,1000Hz 以上呈对数增长,Mel 频率与 Hz 频率的关系为$f_{mel} = 2595 \cdot lg(1+\frac{f}{700Hz})$,如下图所示,图源见一个 MFCC 的介绍教程。有另一种计算方式为$f_{mel} = 1125 \cdot ln(1+\frac{f}{700Hz})$。下面给出一个计算 Mel 声谱图的例子。另,python 中可以用 librosa 调包得到梅尔声谱图。
通过实际的主观实验,科学家发现人耳对低频信号的区别更加敏感,而对高频信号的区别则不那么敏感。也就是说低频段上的两个频度和高频段上的两个频度,人们会更容易区分前者。因此我们就明白了,频域上相等距离的两对频度,对于人耳来说他们的距离不一定相等。那么,能不能调整频域的刻度,使得这个新的刻度上相等距离的两对频度,对于人耳来说也相等呢?答案是可以的,这就是梅尔刻度。
下图展示了梅尔频度-正常频度的对应关系,正如之前所说明的,低频段的部分,梅尔刻度和正常频度几乎呈线性关系,而在高频段,因为人耳的感知变弱,因此两者呈对数关系。
(2)假设现在用 10 个 Mel filterbank(一些论文会用 40 个,如果求 MFCC 一般是用 26 个然后在最后取前 13 个),为了获得 filterbanks 需要选择一个 lower 频率和 upper 频率,用 300 作为 lower,8000 作为 upper 是不错的选择。如果采样率是 8000Hz 那么 upper 频率应该限制为 4000。然后用公式把 lower 和 upper 转为 Mel 频率,我们使用上述第二个公式(ln 那条),可以得到 401.25Mel 和 2834.99Mel。
(3)因为用 10 个滤波器,所以需要 12 个点来划分出 10 个区间,在 401.25Mel 和 2834.99Mel 之间划分出 12 个点,m(i) = (401.25, 622.50, 843.75, 1065.00, 1286.25, 1507.50, 1728.74, 1949.99, 2171.24, 2392.49, 2613.74, 2834.99)。
(4)然后把这些点转回 Hz 频率,h(i) = (300, 517.33, 781.90, 1103.97, 1496.04, 1973.32, 2554.33, 3261.62, 4122.63, 5170.76, 6446.70, 8000)。
(5)把这些频率转为 fft bin,f(i) = floor( (N+1)*h(i)/Fs),N 为 FFT 长度,默认为 512,Fs 为采样频率,默认为 16000Hz,则 f(i) = (9, 16, 25, 35, 47, 63, 81, 104, 132, 165, 206, 256)。这里 256 刚好对应 512 点 FFT 的 8000Hz。
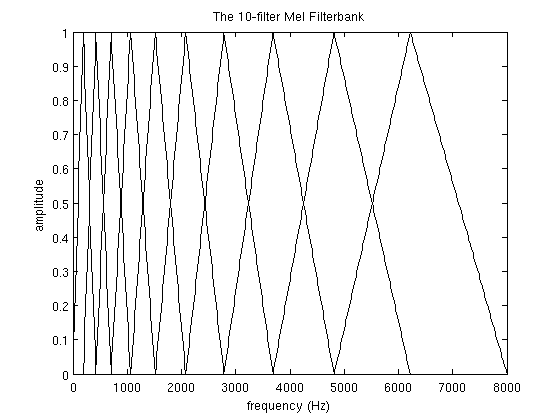
(6)然后创建滤波器,第一个滤波器从第一个点开始,在第二个点到达最高峰,第三个点跌回零。第二个滤波器从第二个点开始,在第三个点到达最大值,在第四个点跌回零。以此类推。滤波器的示意图如下图所示,图源见csdn-MFCC 计算过程。可以看到随着频率的增加,滤波器的宽度也增加。
(7)接下来给出滤波器输出的计算公式,如下所示,其中 m 从 1 到 M,M 表示滤波器数量,这里是 10。k 表示点的编号,一个 fft 内 256 个点,k 从 1 到 256,表示了 fft 中的 256 个频点(k=0 表示直流信号,算进来就是 257 个频点,为了简单起见这里省略 k=0 的情况)。
(8)最后还要乘上 fft 计算出来的能量谱,关于能量谱在前一节(线性)声谱图中已经讲过了。将滤波器的输出应用到能量谱后得到的就是梅尔谱,具体应用公式如下,其中 $|X(k)|^2$表示能量谱中第 k 个点的能量。以每个滤波器的频率范围内的输出作为权重,乘以能量谱中对应频率的对应能量,然后把这个滤波器范围内的能量加起来。举个例子,比如第一个滤波器负责的是 9 和 16 之间的那些点(在其它范围的点滤波器的输出为 0),那么只对这些点对应的频率对应的能量做加权和。
(9)这样计算后,对于一帧会得到 M 个输出。经常会在论文中看到说 40 个梅尔滤波器输出,指的就是这个(实际上前面说的梅尔滤波器输出是权重 H,但是这里的意思应该是将滤波器输出应用到声谱后得到的结果,根据上下文可以加以区分)。然后在时间上堆叠多个 “40 个梅尔滤波器输出” 就得到了梅尔尺度的声谱(梅尔谱),如果再取个 log,就是 log 梅尔谱,log-Mels。
(10)把滤波器范围内的能量加起来,可以解决一个问题,这个问题就是人耳是很难理解两个靠的很近的线性频率(就是和梅尔频率相对应的赫兹频率)之间不同。如果把一个频率区域的能量加起来,只关心在每个频率区域有多少能量,这样人耳就比较能区分,我们希望这种方式得到的(Mel)声谱图可以更加具有辨识度。最后取 log 的 motivation 也是源于人耳的听力系统,人对声音强度的感知也不是线性的,一般来说,要使声音的音量翻倍,我们需要投入 8 倍的能量,为了把能量进行压缩,所以取了 log,这样,当 x 的 log 要翻倍的话,就需要增加很多的 x。另外一个取 log 的原因是为了做倒谱分析得到 MFCC,具体细节见下面 MFCC 的介绍。
MFCC
(1)MFCC,梅尔频率的倒谱系数(Mel Frequency Cepstral Coefficents),是广泛应用于语音领域的特征,在这之前常用的是线性预测系数 Linear Prediction Coefficients(LPCs)和线性预测倒谱系数(LPCCs),特别是用在 HMM 上。
(2)先说一下获得 MFCC 的步骤,首先分帧加窗,然后对每一帧做 FFT 后得到(单帧)能量谱(具体步骤见上面线性声谱图的介绍),对线性声谱图应用梅尔滤波器后然后取 log 得到 log 梅尔声谱图(具体步骤见上面梅尔声谱图的介绍),然后对 log 滤波能量(log 梅尔声谱)做 DCT,离散余弦变换(傅里叶变换的一种),然后保留第二个到第 13 个系数,得到的这 12 个系数就是 MFCC。
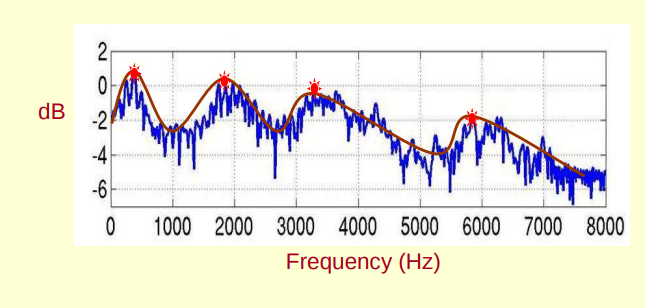
(3)然后再大致说说 MFCC 的含义,下图第一个图(图源见参考资料 [1])是语音的频谱图,峰值是语音的主要频率成分,这些峰值称为共振峰,共振峰携带了声音的辨识(相当于人的身份证)。把这些峰值平滑地连起来得到的曲线称为频谱包络,包络描述了携带声音辨识信息的共振峰,所以我们希望能够得到这个包络来作为语音特征。频谱由频谱包络和频谱细节组成,如下第二个图(图源见参考资料[1])所示,其中 log X[k] 代表频谱(注意图中给出的例子是赫兹谱,这里只是举例子,实际我们做的时候通常都是用梅尔谱),log H[k]代表频谱包络,log E[k]代表频谱细节。我们要做的就是从频谱中分离得到包络,这个过程也称为倒谱分析,下面就说说倒谱分析是怎么做的。
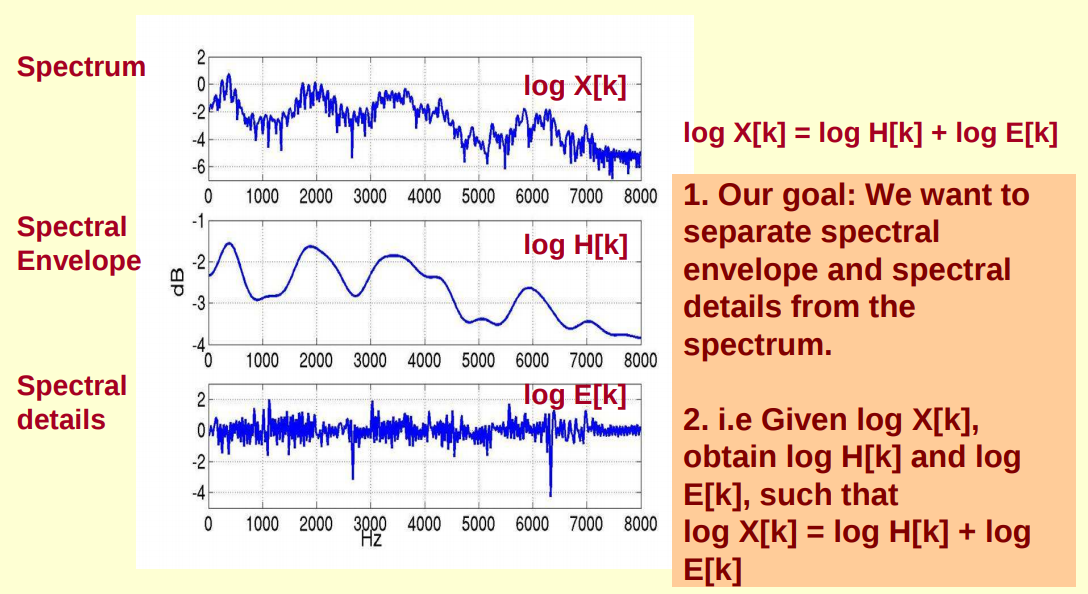
(4)要做的其实就是对频谱做 FFT,在频谱上做 FFT 这个操作称为逆 FFT,需要注意的是我们是在频谱的 log 上做的,因为这样做 FFT 后的结果 x[k]可以分解成 h[k]和 e[k]的和。我们先看下图(图源见参考资料 [1]),对包络 log H[k] 做 IFFT 的结果,可以看成 “每秒 4 个周期的正弦波”,于是我们在伪频率轴上的 4Hz 上给一个峰值,记作 h[k]。对细节 log E[k] 做 IFFT 的结果,可以看成 “每秒 100 个周期的正弦波”,于是我们在伪频率轴上的 100Hz 上给一个峰值,记作 e[k]。对频谱 log X[k] 做 IFFT 后的结果记作 x[k],这就是我们说的倒谱,它会等于 h[k]和 e[k]的叠加,如下第二个图所示。我们想要得到的就是包络对应的 h[k],而 h[k]是 x[k]的低频部分,只需要对 x[k]取低频部分就可以得到了。
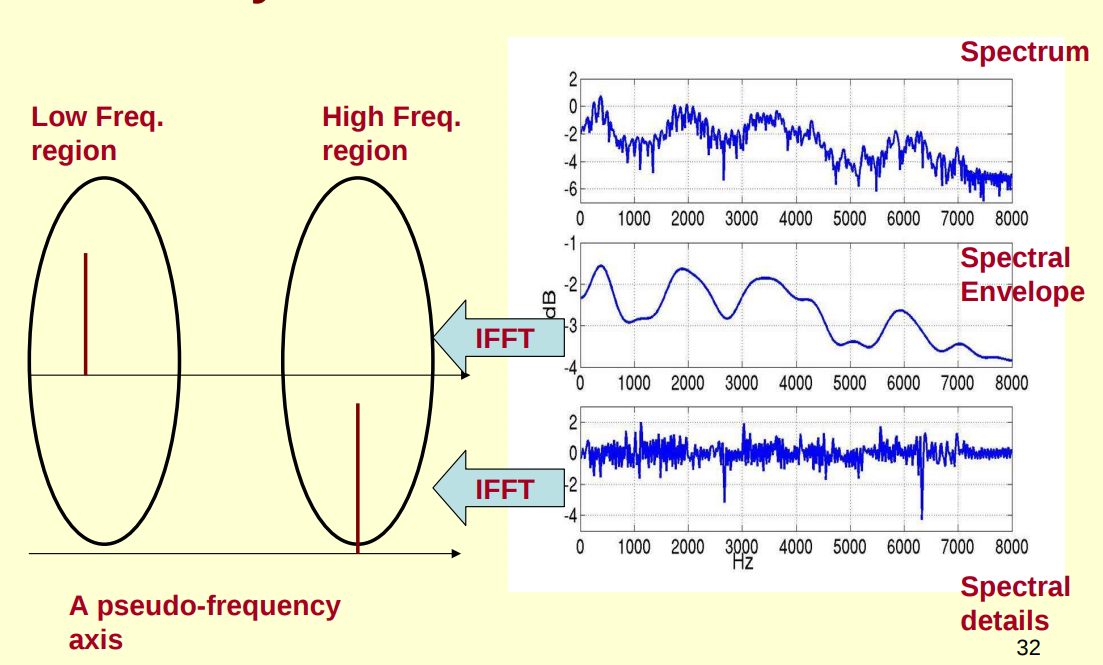

(5)最后再总结一下得到 MFCC 的步骤,求线性声谱图,做梅尔滤波得到梅尔声谱图,求个 log 得到 log 梅尔谱,做倒谱分析也就是对 log X[k] 做 DCT 得到 x[k],取低频部分就可以得到倒谱向量,通常会保留第 2 个到第 13 个系数,得到 12 个系数,这 12 个系数就是常用的 MFCC。图源见参考资料 [1]。

deltas,deltas-deltas
(1)deltas 和 deltas-deltas,看到很多人翻译成一阶差分和二阶差分,也被称为微分系数和加速度系数。使用它们的原因是,MFCC 只是描述了一帧语音上的能量谱包络,但是语音信号似乎有一些动态上的信息,也就是 MFCC 随着时间的改变而改变的轨迹。有证明说计算 MFCC 轨迹并把它们加到原始特征中可以提高语音识别的表现。
(2)以下是 deltas 的一个计算公式,其中 t 表示第几帧,N 通常取 2,c 指的就是 MFCC 中的某个系数。deltas-deltas 就是在 deltas 上再计算以此 deltas。
(3)对 MFCC 中每个系数都做这样的计算,最后会得到 12 个一阶差分和 12 个二阶差分,我们通常在论文中看到的 “MFCC 以及它们的一阶差分和二阶差分” 指的就是这个。
(4)值得一提的是 deltas 和 deltas-deltas 也可以用在别的参数上来表述动态特性,有论文中是直接在 log Mels 上做一阶差分和二阶差分的,论文笔记:语音情感识别(二)声谱图 + CRNN 中 3-D Convolutional Recurrent Neural Networks with Attention Model for Speech Emotion Recognition 这篇论文就是这么做的。
总结
1.频谱:时域信号(一维)短时傅里叶变换后的频域信号(一维)。
2.声谱图/语谱图:把一整段语音信号截成许多帧,把它们各自的频谱“竖”起来(即用纵轴表示频率),用颜色的深浅来代替频谱强度,再把所有帧的频谱横向并排起来(即用横轴表示时间),就得到了语谱图,它可以称为声音的时频域表示。
3.倒谱:也叫做倒频谱,二次谱,对数功率谱等。对声谱图取对数后,再DFT变回时域,此时不是完全意义上的时域,应叫做倒谱域。
4.MFCC:对线性声谱图应用mel滤波器后,取log,得到log梅尔声谱图,然后对log滤波能量(log梅尔声谱)做DCT离散余弦变换(傅里叶变换的一种),然后保留第2到第13个系数,得到的这12个系数就是MFCC。
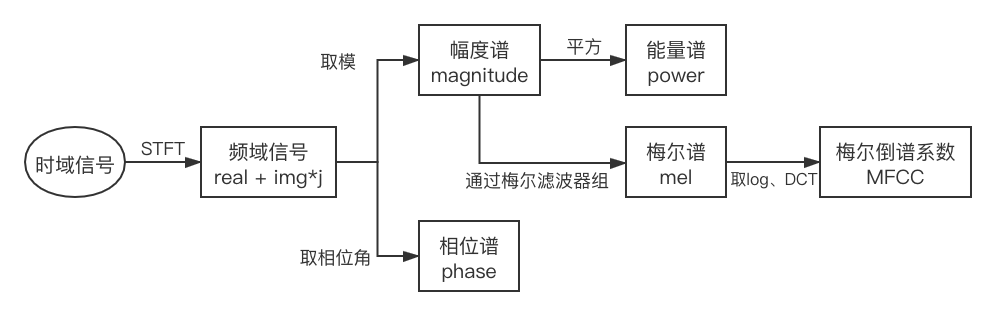
附加:
1.能量谱:也叫做能量密度谱。是原信号傅里叶变化的平方。用于描述时间序列的能量随频率的分布。
2.功率谱:将频谱或时频谱(语谱)中的幅值进行平方,得到功率谱。
3.功率谱密度:定义为单位频带内的吸纳后功率。其推导公式较为复杂,但维纳-辛欣定理证明了:一段信号的功率谱等于这段信号自相关函数的傅里叶变换。
注:信号分为确定和随机,确定信号又分为能量和功率,随机信号一定是功率信号。语音信号是随机信号。
参考资料
[1] CMU 语音课程 slides
[2] 一个 MFCC 的介绍教程
[3] csdn-MFCC 计算过程
[4] 博客园 - MFCC 学习笔记
参考
cnlinxi/book-text-to-speech: A book about Text-to-Speech (TTS) in Chinese. (github.com)
声谱图,梅尔语谱,倒谱,梅尔倒谱系数
论文笔记:语音情感识别(四)语音特征之声谱图,log梅尔谱,MFCC,deltas
语音基础知识(附相关实现代码)
不同元音辅音在声音频谱的表现是什么样子? - 王赟 Maigo的回答 - 知乎
搬运工:波形、频谱和声谱的关系
语音合成基础(3)——关于梅尔频谱你想知道的都在这里
语音合成基础(1)——语音和TTS
《语音信号处理》整理
MP3的采样率和比特率

