Wishart距离定义
根据之前文章的分析,multi-look POLSAR像素$\rm \langle T \rangle$能够根据Wishart距离$d\left(\langle \rm{T} \rangle | \langle \rm{T}_m \rangle \right)$分类,正如下面公式所示:
其中,$Trace(\cdot)$是矩阵的迹,$\cdot ^{-1}$是矩阵的逆,$|\cdot|$是矩阵的行列式,$ \langle \rm{T}_m \rangle$是由训练集的第$m$类评估得到,可以视为第$m$类的聚类中心。通过计算一个像素点与所有类聚类中心的距离,距离最近的类即为该像素点所属的类别。
对于无监督训练,可以先使用聚类的方法得到不同类别的数据;而对于有监督训练,训练集中已经包含了不同类别的训练数据。因此$\langle \rm{T}_m \rangle$可以使用如下公式得到:
其中,$\Omega_m$是第$m$类的像素集合,而$|\Omega_m|$是$\Omega_m$的像素总数。
快速实现
根据论文[1]中的描述,传统Wishart距离的运算需要使用两层for循环,第一层for循环对应类别,第二层for循环对应于每一个像素点。而且公式$({1})$中含有矩阵运算,因此传统计算Wishart距离的方法计算量特别大。该论文针对这个问题,提出了针对Wishart距离的一种特殊的线性变换方式。
正如$({1})$中所见,Wishart距离计算方式有两项,分别是$Trace \left( \langle \rm{T}_m \rangle^{-1} \langle \rm{T} \rangle \right)$和$ ln| \langle \rm{T}_m \rangle|$。令$\Gamma=\langle \rm{T}_m \rangle^{-1} \langle \rm{T} \rangle$,只有对角元素是需要的,而其他的元素是富余的。
令$\sigma=f(\sum)$为对矩阵$\sum$按列拉成一个列向量。例如$f(\langle \rm{T} \rangle)=\left[T_{11} , \overline{T_{12}}, \overline{T_{13}}, T_{12}, T_{22}, \overline{T_{23}} , T_{13}, T_{23}, T_{33} \right]’$。令$\sum=f^{-1}(\sigma)$为$\sigma=f(\sum)$的逆函数。
假设一共有$M$类,令$W=\left[w_1, w_2, \cdots, w_M \right]$,其中$w_m=f \left( \left( \langle \rm{T}_m \rangle^{-1}\right)’\right)$,$m=1,2,\cdots,M$。因为函数$\sigma=f(\sum)$是按列将矩阵拉成列向量的,所以需要对$\langle \rm{T}_m \rangle^{-1}$求转置。
假设一共有$N$个样本,第$i$个样本的矩阵形式可以使用$\langle \rm T^i \rangle$表示,而$t_i=f(\langle \rm T^i \rangle)$。那么可得到下式
其中,$w_m$和$t_i$均为9维复数列向量。$(w_m)’$为$w_m$的转置(非共轭转置0)。等号右边的运算只需要9次乘法和8次加法,大概只为等号左边运算量的三分之一。
可以这样理解,上面对矩阵乘积的结果求迹就相当于$\sum_{j=1}^J第一个矩阵的第j行\times 第二个矩阵的第j列$,其中$J$表示矩阵的维度均为$J \times J$。
另外,我们令
$b$为列向量。因此某一个像素点$t$到不同聚类中心的Wishart距离可以通过如下线性变换得到计算得到,其中$t=f(\langle \rm T \rangle)$。
而所有的像素点到不同聚类中心的Wishart距离可以用下面式子得到:
其中$B=\left[b, b, \cdots, b \right]$,即重复$b$共N次。$W’$的维度为$[M,9]$,而$T$的维度为$[9,N]$,而$B$的维度为$[M,N]$。所以$D$的维度为$[M,N]$,具体表达式如下。其中$D(m,n)$表示第$n$个像素点$\langle \rm{T}^n \rangle$距离第$m$个聚类中心$\langle \rm{T}_M \rangle$的Wishart距离。
通过这种方式,所有的像素点到不同聚类中心的Wishart距离不需要借助for循环即可实现。
对于$\langle \rm T \rangle$,加上上标表示某一个样本,加上下标表示某一类的聚类中心。
传统Wishart距离计算方式和线性变换Wishart距离计算方式对比如下图所示。

Wishart Network
定义
该网络由论文[1]中所提到,这里做一个简单的总结。
Wishart分类器的精度主要取决于每一类聚类中心的好坏。假设有类标的训练集集合大小为$K$,可以表示为$\Omega=\left\{ \left( t_1^l, y_1^l \right), \left( t_2^l, y_2^l \right), \cdots, \left( t_K^l, y_K^l \right) \right\}$,其中$t_k^l, k=1,2,\dots,K$表示第$k$个有类标的像素且$t_k^l=f(\langle \rm T^k \rangle)$,$y_k^l$表示对应的one-hot类标。给定一个POLSAR像素点$t, t=f(\langle \rm T \rangle)$,可以根据下式对其类标进行预测:
其中,$W$和$b$的定义与快速实现小节的定义相同,$sigm(\alpha)=\frac{1}{1+exp(-\alpha)}$。$U$和$c$的分别为权重和偏置参数,$y$为预测出的类标,维度为$[M,1]$,最大值对应的下标即为预测出的类别。如果$W$没有更新,$W’t+b$表示像素$t$到各个聚类中心的距离。
对应的损失函数如下,其中$y_k=g(t_k^l)$
$\Omega$中的$l$表示训练集的意思,以区分与
快速实现小节的所有样本。
在式子$({8})$中,$t=f(\langle \rm T \rangle)$为复数数据;$W$为复数矩阵,每一类的聚类中心为一列,维度为$[9, M]$(非转置后的维度);$b=\left[ ln(|\langle \rm{T}_1 \rangle|), ln(|\langle \rm{T}_2 \rangle|) , \cdots, ln(|\langle \rm{T}_M \rangle|) \right]’$为实值列向量,维度为$[M,1]$;$W’t+b$为实值向量对应于Wishart距离;$U$和$c$均为实值矩阵,维度分别为$[M,M]$和$[M,1]$。
实际上,$W’t+b$求出的是实数向量,但是由于误差的存在,通常会存在虚部,所以在代码中实际上通过$sigm\left(Re \left(W’t+b \right)\right)$实现了实数向量。
为了表述方便,文中令$h=sigm\left( W’t+b \right)$。
可能是为了求导方便,原论文对式子$({8})$做了进一步的简化,令$\widetilde t=[t;1]$,维度为$[10,1]$;$\widetilde W=[W;b’]$,$\widetilde W’=[W’,b]$,维度为$[M,10]$;$\widetilde h=[h;1]$,维度为;$\widetilde U=[U;c’]$,$\widetilde U’=[U’,c]$,维度为[M,M+1]。则式子$({8})$可以写成下面式子:
那么损失函数可以定义为:
其中,$\widetilde{h_k}=[h_k;\vec 1]=\left[ sigm(\widetilde W’\widetilde{t_k});\vec 1 \right]$,$\widetilde{t_k}=[t_k;1]$。
训练
在Wishart Network中,一共有$\widetilde W$和$\widetilde U$两个可训练参数,我们采用如下方式初始化:
- 对于$\widetilde W$,首先利用公式$({2})$得到$ \langle \rm{T}_m \rangle$,然后得到$W$中的每一列$w_m=f \left( \left( \langle \rm{T}_m \rangle^{-1}\right)’\right)$。对于$b$,采用公式$({4})$进行初始化,然后$\widetilde W=[W;b’]$。
- 对于$\widetilde U$,给定了$\widetilde W$后,可以计算得到$\widetilde{h_k}$,由最小二乘法可以得到$\widetilde{U}$的解析解为$\widetilde{U}=\sum_{k=1}^K\left(\widetilde{h_k} \widetilde{h’_k} \right)^{-1} \widetilde{h_k} y_k^{l’}$。
对于每次更新时:
- 对于$\widetilde W$,利用反向传播求得梯度后,利用公式$\widetilde W = \widetilde W - \lambda \frac{\delta E}{\delta \widetilde W }$,其中$\lambda$为步长。值得注意的是,在$\widetilde W $中$b_m=\widetilde W(10,m)$,我们其实并没有用到$\widetilde W(10,m)$,而是采用了$b_m=ln| \langle \rm{T}_m \rangle|$的方式计算。这个小细节在Wishart Network中特别重要。
- 对于$\widetilde U$,给定了$\widetilde W$后,还是采用最小二乘法的方式得到更新值。
正如上面我个人批注的,上面在得到Wishart距离时采用了$sigm\left(Re \left(W’t+b \right)\right)$得到的实值向量。论文对应的代码在更新$\widetilde W$时,只取了$\frac{\delta E}{\delta \widetilde W }$的实部而抛弃了虚部,所以$\widetilde W$也只是更新了实部。
我们令$T^l=\left[ t_1^l, t_2^l, \cdots, t_K^l \right]$,$Y_l=\left[ y_1^l, y_2^l, \cdots, y_K^l \right]$,则Wishart Network的整体训练流程如下:

需要强调的是,Wishart Network和普通网络的区别在于:
- 输入$t$是复数数据
- $W$和$b$的初始化是特殊的
- $b$的更新是特殊的
定义了Wishart Network后,可以得到有三个module的DSN,整体结构如下:
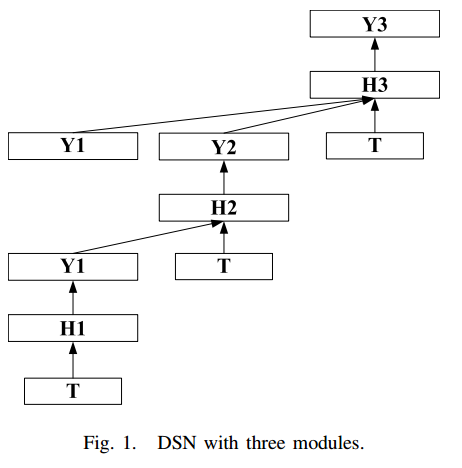
对于DSN,具体内容请看下面的论文[0],我这里只说明要注意的几点:
- DSN的三个module是逐层训练的,即先训练第一个module,然后再训练第二个module,最后再训练第三个module
- 后一个module的输入由前面所有底层的输出+训练数据组成的。
参考
[1] Wishart Deep Stacking Network for Fast POLSAR Image Classification

