半监督学习可以利用“少”的有标记样本和“多”的无标记样本改善分类器的性能,在一定程度上提高学习能力,成为当前机器学习研究领域的热点问题。
半监督学习机理
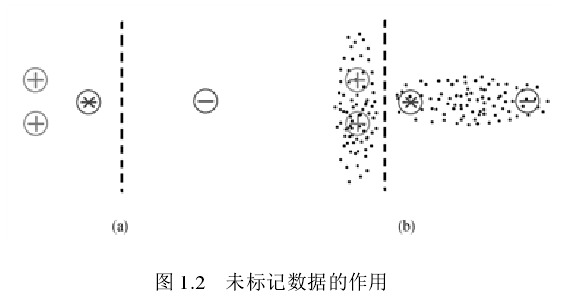
下图给出了一个缺少概念标记的未标记数据为何能够帮助学习器学习的简单例子。用“+”表示正样本、“-”表示负样本、“.”表示未标记样本。现在需要预测“*”这个样本的标记。当仅利用有标记样本进行学习(如图 1.2(a)所示)时,会很自然地将该样本判为正样本;但若考虑大量未标记样本(如图 1.2(b)所示)的分布,则可以发现待预测样本和有标记的负样本同属于一个簇,由于处于同一个簇中样本的性质应该相似,因此将该样本预测为负样本应更加合理。从此例可以看出,未标记样本提供的分布信息能够帮助和指导学习过程。
半监督学习假设
一般情况下需要在某些假设的基础上建立未标记样本和目标的联系,来辅助提高学习性能。目前,半监督学习框架下有流形假设(manifold assumption) 和聚类假设(cluster assumption)两个常用的基本假设。
流形假设反映了判别函数的局部平滑性,指处于同一个小的局部邻域内的样本应该相似,因此,其标记也应该相同。在这一假设下,海量未标记样本的作用就是更加准确地刻画局部区域的分布特性,使得判别函数更好地进行拟合。
聚类假设是指处于相同聚类(cluster)中的样本属于同一类别的可能性较大。根据该假设,未标记样本就是用来探明样本空间中稀疏和稠密区域,指导决策边界尽量通过稀疏区域,避免把稠密的数据点分到决策边界两侧,调整决策边界。
一般情形下的聚类假设和流形假设是一致的。满足流形假设的模型能够在数据稠密的聚类中得到相似的输出。然而,由于流形假设的同一邻域样本具有相似的输出而不是相同的标记,因此流行假设比聚类假设更为一般。
半监督分类方法
半监督学习按照学习任务的不同可以分为半监督分类和半监督聚类。半监督分类利用大量的无标记数据和少量标记样本作为训练集训练更好的分类器。半监督聚类则是利用少量标记样本或者约束信息辅助聚类,指导聚类过程,以提高聚类算法的效果。下面将分别介绍目前常用的半监督分类方法。
目前主要的半监督分类方法有:基于生成模型(Generative Models)的方法、基于自训练(Self-Training)的方法、基于协同训练(Co-training)的方法、基于低密度划分(Avoiding Changes in Dense Regions)的方法、基于图(Graph-Based Methods)的方法等。
基于生成模型的半监督学习方法
基于生成模型的半监督学习方法通常是把未标记样本属于每个类别的概率看成一组缺失参数,然后采用期望最大化(expectation maximization) 算法对缺失参数进行极大似然估计。不同的基于 GM 方法的区别在于选择了不同的生成式模型作为基分类器,例如朴素贝叶斯(naive Bayes)、混合专家 (mixture of experts)、混合高斯(mixture of Gaussians)。由于寻找合适的生成式模型来为数据建模需要大量领域知识,这使得基于生成式模型的半监督学习在实际问题中的应用有限。虽然基于生成式模型的半监督学习方法简单、直观,但是当模型假设与数据分布不一致时,大量的未标记数据的使用来估计模型参数反而会降低模型的泛化能力。
自训练半监督学习方法
在自训练中分类器首先通过少量的有标记样本学习到一个分类器,然后利用这个分类器对未标记样本分类,将得到的高置信样本及其标记加入到训练集中重新训练分类器。重复此过程直至算法稳定。显然,分类器的错误也会累积。一些算法会通过设定阈值,小于阈值的样本不会加入到训练集中。
协同训练半监督学习方法
协同训练有三个假设:(i) 特征集能被分成两个特征子集 ;(ii) 每个特征子集都可以训练一个好的分类器 ;(iii) 在给定类标时两个子集条件独立。初始时分别利用有标记样本在两个特征子集上训练两个分类器,然后每个分类器对未标记样本进行分类,使用另一分类器得到的高置信度的样本及其标记进行再训练,循环直至算法稳定。协同训练可以避免自训练中的自身错误积累,但是该算法对样本特征要求较高,会造成未标记样本采集费用的增加。
基于低密度划分的半监督学习方法
该类方法要求决策边界尽量通过数据较为稀疏区域,以免把聚类中稠密的数据点分到决策边界两侧。基于该思想,Joachims提出了 TSVM 算法。在训练过程中,TSVM 算法首先利用有标记的数据训练一个 SVM 并估计未标记数据的标记,然后基于最大化间隔准则,迭代式地交换分类边界两侧样本的标记,使得间隔最大化,并以此更新当前预测模型,从而实现在尽量正确分类有标记数据的同时,将决策边界“推”向数据分布相对稀疏的区域。然而,TSVM 的损失函数非凸,学习过程会因此陷入局部极小点,从而影响泛化能力。为此,多种 TSVM 的变体方法被提出,以缓解非凸损失函数对优化过程造成的影响,典型方法包括确定性退火、CCCP 直接优化等。此外,低密度划分思想还被用于 TSVM 以外的半监督学习方法的设计,例如通过使用熵对半监督学习进行正则化,迫使学习到的分类边界避开数据稠密区域。
基于图的半监督学习方法
该类方法利用有标记和未标记数据构建数据图,并且基于图上的邻接关系将标记从有标记的数据点向未标记数据点传播。根据标记传播方式可将基于图的半监督学习方法分为两大类,一类方法通过定义满足某种性质的标记传播方式来实现显式标记传播,例如基于高斯随机场与谐函数的标记传播、基于全局和局部一致性的标记传播等;另一类方法则是通过定义在图上的正则化项实现隐式标记传播,例如通过定义流形正则化项,强制预测函数对图中的近邻给出相似输出,从而将标记从有标记样本隐式地传播至未标记样本。事实上,标记传播方法对学习性能的影响远比不上数据图构建方法对学习性能的影响大。如果数据图的性质与数据内在规律相背离,无论采用何种标记传播方法,都难以获得满意的学习结果。然而,要构建反映数据内在关系的数据图,往往需要依赖大量领域知识。所幸,在某些情况下,仍可根据数据性质进行处理,以获得鲁棒性更高的数据图,例如当数据图不满足度量性时,可以根据图谱将非度量图分解成多个度量图,分别进行标记传播,从而可克服非度量图对标记传播造成的负面影响[2]。
流形引言
若只有监督学习的话,在拿到较少样本的时候,只是在几类数据点间找到了一个分类面,但是这个分类面不一定是包含了数据真实的分布信息的。如下图所示,只是在两个样本点中,找到了一个分类面。此时对于新来的样本,分对分错的概率基本都是0.5,
但是如果加入了数据分布的信息,也就是说只要知道样本是一个什么样子的分布,而不一定要把每一个分布的点都打上标签,这样得到的分类面就比较精确了,如下图所示:
若能给有监督的样本给出足够的样本分布信息,那么分类能力就可以得到提升和保证了。而找出分布信息就是无监督学习最擅长做的事。换句话说,我们要给无监督学习学到的分布信息帖上少量有监督的标签,这也就是半监督学习要做的主要工作。在流形正则化中,就是通过流形正则化项来达到结合有监督和无监督样本来找出分布特征的目的。
下面进行详细介绍。
流形数据
机器学习中的流形借用了数学中流形的概念,但机器学习并不真的去研究拓扑。更多的时候,机器学习中的流形是指数据分布在高维空间中的一个低维度的流形上面,意思就是数据本质上不是高维度的(所以处理起来不会像真正的高维数据一样困难)。如图:

数据看似分布在一个三维空间中,而实际上则是分布在一个卷曲的二维平面上,也就是数据的真实分布其实只有二维。直接在原始数据的高维空间中采用机器学习中的分类/回归方法,往往会面对高维度带来的模型高复杂度问题,导致模型的泛化能力下降,所以如果能够讲数据合理得展开在低维空间中,那么能够大大简化模型复杂度。
很多真实数据都具备类似的性质,比如:同一张正面人脸在不同光照环境下的图像集。
流形的概念很早就被引入到机器学习中,例如流行学习:假设数据是均匀采样于一个高维欧氏空间中的低维流形,流形学习就是从高维采样数据中恢复低维流形结构(也就是把上面这种三维卷曲摊开,放在二维平面上),即找到高维空间中的低维流形,并求出相应的嵌入映射,以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质,找到产生数据的内在规律。包括PCA(Principal Components Analysis)、LLE(Locally Linear Embedding)、MDS(Multidimensional Scaling)、Isomap、KPCA等。这里附录一张对于数据降维的总结。
流形正则化
『流形正则化』其实就是在机器学习问题中的正则化项中加入和流形相关的项,利用数据中的几何结构,起到半监督的作用,比如:两个样本在流形中距离相近,那么他们的label也应该一样或相似。参考paper: Manifold Regularization: A Geometric Framework for Learning from Labeled and Unlabeled Examples
一个一般的机器学习有监督优化问题可以形式化成这样(式子都来自于上面的参考):
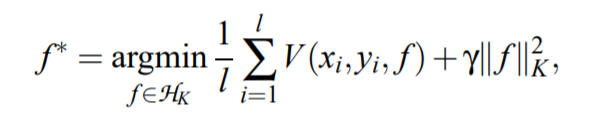
其中第一项是经验误差,第二项是正则化项(RKHS表示),而加入了流形正则化的优化问题可以形式化成:

其实就是多了最后一项,作用是约束 $f$ 的输出使得输出的$y$符合样本$x$的分布所代表的几何结构。约束 $f$ 输出的项可以是各种各样的,比如常见的graph regularization:
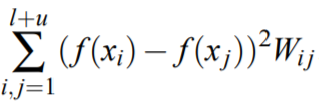
其中 $W_{ij}$ 表示$i$和$j$两个样本之间在流形上的近似度,$l、u$分别表示有监督样本和无监督样本集合,将其表示成矩阵形式如下:
假设每个样本的特征维度为$M$,则$X \in \mathbb R^{(l+u)\times M}$,$D$为对角矩阵且$D_{ii}=\sum_j W_{ij}$,$L=D-W$为无向图的非标准化图拉普拉斯。
加入的流形正则化项可以这样理解:从它的假设——已知样本相似的数据则对于的标签也有相似性(两个样本在流形中距离相近,那么他们的label也应该一样或相似。)。那么最后一个公式就保证训练的$f$满足这种关系(样本的分布函数),而不仅仅是保证很高的分类能力。无监督学习就是学习样本的分布,监督学习是寻找一个最优的分界面,流形正则化则是减弱监督学习的使之带有无监督学习的优点。
流形正则化有这么几个作用:
- 利用样本的空间分布信息
- 给有监督模型加流形正则化,可以尽可能多得利用无监督的数据,使得模型转化为半监督模型
参考
[1] 王秀秀. 2013. 《基于稀疏图的半监督学习方法研究》.
[2] Zhang Y, Zhou Z H. Non-metric label propagation[C]//Twenty-First International Joint Conference on Artificial Intelligence. 2009.
流形学习-高维数据的降维与可视化
有谁给解释一下流形以及流形正则化? - li Eta的回答 - 知乎
流形正则化公式的理解
流形正则化学习笔记

